Vad är ett lågpassfilter? En handledning om grunderna för passiva RC-filter

december 5, 2021admin

Vad är filtrering? Lär dig vad lågpassfilter med motståndskapacitor (RC) är och var du kan använda dem.

Denna artikel introducerar begreppet filtrering och förklarar i detalj syftet med och egenskaperna hos lågpassfilter med motståndskapacitor (RC).

Tidsdomän och frekvensdomän

När du tittar på en elektrisk signal på ett oscilloskop ser du en linje som representerar spänningsförändringar i förhållande till tiden. Vid varje specifik tidpunkt har signalen endast ett spänningsvärde. Det du ser på oscilloskopet är tidsdomänrepresentationen av signalen.

En typisk oscilloskopspårning är okomplicerad och intuitiv, men den är också något restriktiv, eftersom den inte direkt avslöjar frekvensinnehållet i en signal. Till skillnad från tidsdomänrepresentationen, där en tidpunkt motsvarar endast ett spänningsvärde, förmedlar en frekvensdomänrepresentation (även kallad spektrum) information om en signal genom att identifiera de olika frekvenskomponenter som är närvarande samtidigt.

Tidsdomänrepresentationer av en sinusoid (överst) och en fyrkantig våg (nederst).

Frekvensdomänrepresentationer av en sinusoid (överst) och en fyrkantsvåg (nederst).

Vad är ett filter?

Ett filter är en krets som tar bort, eller ”filtrerar bort”, ett visst intervall av frekvenskomponenter. Med andra ord separerar den signalens spektrum i frekvenskomponenter som kommer att passera och frekvenskomponenter som kommer att blockeras.

Om du inte har mycket erfarenhet av frekvensområdesanalys kanske du fortfarande är osäker på vad dessa frekvenskomponenter är och hur de samexisterar i en signal som inte kan ha flera spänningsvärden samtidigt. Låt oss titta på ett kort exempel som hjälper till att klargöra detta begrepp.

Låt oss tänka oss att vi har en ljudsignal som består av en perfekt 5 kHz sinusvåg. Vi vet hur en sinusvåg ser ut i tidsdomänen, och i frekvensdomänen ser vi inget annat än en frekvens ”spik” vid 5 kHz. Låt oss nu anta att vi aktiverar en 500 kHz-oscillator som introducerar högfrekvent brus i ljudsignalen.

Signalen som ses på ett oscilloskop kommer fortfarande att bestå av endast en sekvens av spänningar, med ett värde per tidpunkt, men signalen kommer att se annorlunda ut eftersom dess variationer i tidsdomänen nu måste återspegla både 5 kHz-sinusvågen och de högfrekventa brusfluktuationerna.

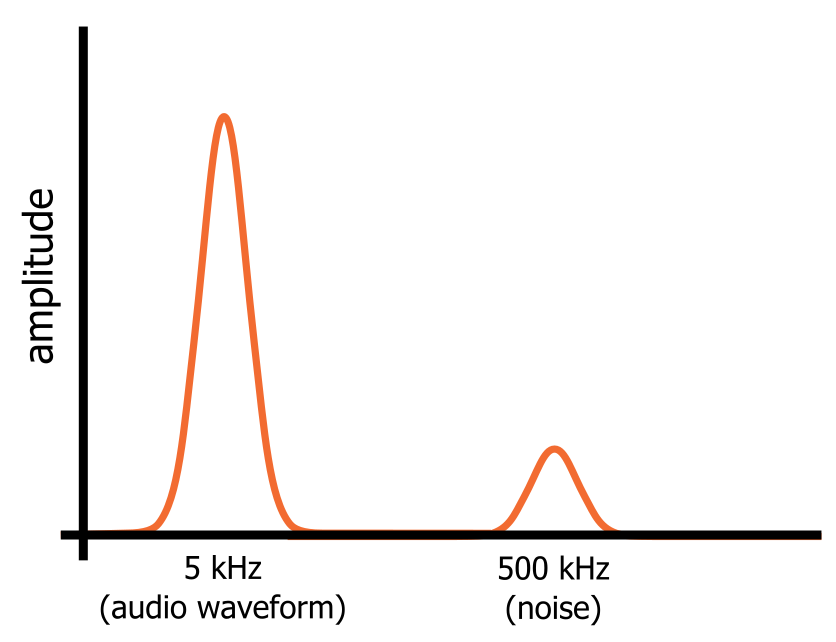
I frekvensdomänen är dock sinusvågen och bruset separata frekvenskomponenter som är närvarande samtidigt i den här enda signalen. Sinusvågen och bruset upptar olika delar av signalens frekvensdomänrepresentation (som visas i diagrammet nedan), och detta innebär att vi kan filtrera bort bruset genom att leda signalen genom en krets som släpper igenom låga frekvenser och blockerar höga frekvenser.

Typer av filter

Filter kan placeras in i breda kategorier som motsvarar de generella egenskaperna hos filterets frekvensgång. Om ett filter släpper igenom låga frekvenser och blockerar höga frekvenser kallas det för ett lågpassfilter. Om det blockerar låga frekvenser och släpper igenom höga frekvenser är det ett högpassfilter. Det finns också bandpassfilter, som bara släpper igenom ett relativt smalt frekvensområde, och bandstoppfilter, som bara blockerar ett relativt smalt frekvensområde.

Filter kan också klassificeras enligt de typer av komponenter som används för att genomföra kretsen. Passiva filter använder motstånd, kondensatorer och induktorer; dessa komponenter har ingen förmåga att ge förstärkning, och följaktligen kan ett passivt filter endast bibehålla eller minska amplituden hos en insignal. Ett aktivt filter kan å andra sidan både filtrera en signal och tillämpa förstärkning, eftersom det innehåller en aktiv komponent såsom en transistor eller en operationsförstärkare.

Detta aktiva lågpassfilter är baserat på den populära Sallen-Key-topologin.

Den här artikeln utforskar analysen och konstruktionen av passiva lågpassfilter. Dessa kretsar spelar en viktig roll i en mängd olika system och tillämpningar.

Det RC-lågpassfilter

För att skapa ett passivt lågpassfilter måste vi kombinera ett resistivt element med ett reaktivt element. Med andra ord behöver vi en krets som består av ett motstånd och antingen en kondensator eller en induktor. Teoretiskt sett är lågpassetopologin för motstånd och induktor (RL) likvärdig, när det gäller filtreringsförmåga, med lågpassetopologin för motstånd och kondensator (RC). I praktiken är dock resistor-kondensator-versionen mycket vanligare, och följaktligen kommer resten av den här artikeln att fokusera på RC-lågpassfiltret.

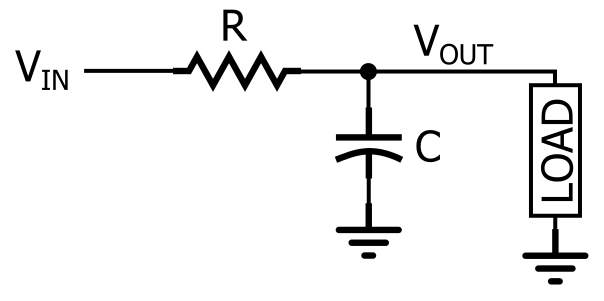
RC-lågpassfiltret.

Som du kan se i diagrammet skapas ett RC-lågpassrespons genom att placera ett motstånd i serie med signalvägen och en kondensator parallellt med lasten. I diagrammet är belastningen en enda komponent, men i en riktig krets kan det vara något mycket mer komplicerat, t.ex. en analog-till-digitalomvandlare, en förstärkare eller ingångssteget i oscilloskopet som du använder för att mäta filtrets respons.

Vi kan intuitivt analysera filtreringsåtgärden i RC-lågpass-topologin om vi inser att motståndet och kondensatorn bildar en frekvensberoende spänningsdelare.

RC-lågpassfiltret omritat så att det ser ut som en spänningsdelare.

När frekvensen på ingångssignalen är låg är kondensatorns impedans hög i förhållande till motståndets impedans; därför faller den största delen av ingångsspänningen över kondensatorn (och över belastningen, som är parallell med kondensatorn). När ingångsfrekvensen är hög är kondensatorns impedans låg i förhållande till motståndets impedans, vilket innebär att mer spänning faller över motståndet och mindre överförs till belastningen. Således passerar låga frekvenser och höga frekvenser blockeras.

Denna kvalitativa förklaring av RC-lågpassfunktionalitet är ett viktigt första steg, men den är inte särskilt hjälpsam när vi faktiskt måste konstruera en krets, eftersom termerna ”högfrekvens” och ”lågfrekvens” är extremt vaga. Ingenjörer måste skapa kretsar som släpper igenom och blockerar specifika frekvenser. I det audiosystem som beskrivs ovan vill vi till exempel bevara en 5 kHz-signal och undertrycka en 500 kHz-signal. Detta innebär att vi behöver ett filter som övergår från att släppa igenom till att blockera någonstans mellan 5 kHz och 500 kHz.

Klippfrekvensen

Det frekvensområde för vilket ett filter inte orsakar någon betydande dämpning kallas för passband, och det frekvensområde för vilket filtret orsakar en betydande dämpning kallas för stoppband. Analoga filter, t.ex. RC-lågpassfilter, övergår alltid gradvis från passband till stoppband. Detta innebär att det är omöjligt att identifiera en frekvens vid vilken filtret slutar släppa igenom signaler och börjar blockera signaler. Ingenjörer behöver dock ett sätt att på ett bekvämt och kortfattat sätt sammanfatta ett filters frekvensgång, och det är här begreppet avgränsningsfrekvens kommer in i bilden.

När du tittar på en plott av ett RC-filters frekvensgång kommer du att märka att termen ”avgränsningsfrekvens” inte är särskilt korrekt. Bilden av att signalens spektrum ”skärs” i två halvor, varav den ena behålls och den andra kasseras, stämmer inte, eftersom dämpningen ökar gradvis när frekvenser rör sig från under gränsen till över gränsen.

Gränsfrekvensen för ett RC-lågpassfilter är i själva verket den frekvens vid vilken amplituden för ingångssignalen minskas med 3 dB (detta värde valdes eftersom en minskning av amplituden med 3 dB motsvarar en minskning av effekten med 50 %). Avgränsningsfrekvensen kallas därför också för -3 dB-frekvensen, och i själva verket är detta namn mer korrekt och mer informativt. Termen bandbredd avser bredden på ett filters passband, och när det gäller ett lågpassfilter är bandbredden lika med -3 dB-frekvensen (vilket visas i diagrammet nedan).

Detta diagram förmedlar de generiska egenskaperna hos frekvensresponsen för ett RC-lågpassfilter. Bandbredden är lika med -3 dB-frekvensen.

Som förklarats ovan orsakas lågpassbeteendet hos ett RC-filter av interaktionen mellan motståndets frekvensoberoende impedans och kondensatorns frekvensberoende impedans. För att bestämma detaljerna i ett filters frekvensrespons måste vi matematiskt analysera förhållandet mellan motstånd (R) och kapacitans (C), och vi kan också manipulera dessa värden för att konstruera ett filter som uppfyller exakta specifikationer. Brytningsfrekvensen (fC) för ett RC-lågpassfilter beräknas på följande sätt:

Låt oss titta på ett enkelt konstruktionsexempel. Kondensatorvärden är mer restriktiva än motståndsvärden, så vi börjar med ett vanligt värde på kapacitansen (t.ex. 10 nF), och sedan använder vi ekvationen för att bestämma det nödvändiga motståndsvärdet. Målet är att konstruera ett filter som bevarar en ljudvågform på 5 kHz och avvisar en brusvågform på 500 kHz. Vi provar en gränsfrekvens på 100 kHz, och senare i artikeln kommer vi att noggrannare analysera effekten av detta filter på de två frekvenskomponenterna.

Sålunda kommer ett motstånd på 160 Ω i kombination med en kondensator på 10 nF att ge oss ett filter som närmar sig det önskade frekvensomfånget.

Beräkning av filterrespons

Vi kan beräkna det teoretiska beteendet hos ett lågpassfilter genom att använda en frekvensberoende version av en typisk spänningsdelareberäkning. Utgången av en resistiv spänningsdelare uttrycks på följande sätt:

RC-filtret använder sig av en likvärdig struktur, men istället för R2 har vi en kondensator. Först ersätter vi R2 (i täljaren) med kondensatorns reaktans (XC). Därefter måste vi beräkna storleken på den totala impedansen och placera den i nämnaren. Således har vi

Reaktansen hos en kondensator anger storleken på motståndet mot strömflödet, men till skillnad från motståndet beror storleken på motståndet på frekvensen hos den signal som passerar genom kondensatorn. Vi måste alltså beräkna reaktansen vid en viss frekvens, och ekvationen som vi använder för detta är följande:

I konstruktionsexemplet ovan är R ≈ 160 Ω och C = 10 nF. Vi antar att amplituden för VIN är 1 V, så att vi helt enkelt kan ta bort VIN från beräkningen. Låt oss först beräkna amplituden för VOUT vid sinusvågens frekvens:

Amplituden för sinusvågen är i stort sett oförändrad. Det är bra, eftersom vår avsikt var att bevara sinusvågen och samtidigt undertrycka bruset. Detta resultat är inte förvånande, eftersom vi valde en gränsfrekvens (100 kHz) som är mycket högre än sinusvågens frekvens (5 kHz).

Nu ska vi se hur framgångsrikt filtret kommer att dämpa bruskomponenten.

Brusamplituden är bara cirka 20 % av sitt ursprungliga värde.

Visualisering av filterresponsen

Det bekvämaste sättet att utvärdera ett filters effekt på en signal är att undersöka en plott av filtrets frekvensrespons. Dessa grafer, som ofta kallas Bode-plottar, har storleken (i decibel) på den vertikala axeln och frekvensen på den horisontella axeln; den horisontella axeln har vanligtvis en logaritmisk skala, så att det fysiska avståndet mellan 1 Hz och 10 Hz är detsamma som det fysiska avståndet mellan 10 Hz och 100 Hz, mellan 100 Hz och 1 kHz, och så vidare. Denna konfiguration gör det möjligt att snabbt och noggrant bedöma ett filters beteende över ett mycket stort frekvensområde.

Ett exempel på en frekvensresponsdiagram.

Varje punkt på kurvan anger den magnitud som utdatasignalen kommer att ha om ingångssignalen har en magnitud på 1 V och en frekvens som är lika med motsvarande värde på den horisontella axeln. Till exempel, när ingångsfrekvensen är 1 MHz kommer utgångsamplituden (om man antar att ingångsamplituden är 1 V) att vara 0,1 V (eftersom -20 dB motsvarar en minskning med en faktor tio).

Den generella formen på den här frekvens-respons-kurvan kommer att bli mycket bekant när du tillbringar mer tid med filterkretsar. Kurvan är nästan helt platt i passbandet, och sedan börjar den sjunka snabbare när ingångsfrekvensen närmar sig cutoff-frekvensen. Så småningom stabiliseras förändringstakten i dämpningen, kallad roll-off, vid 20 dB/decad – det vill säga att magnituden av utsignalen minskas med 20 dB för varje faktor tio ökning av ingångsfrekvensen.

Bedömning av lågpassfiltrets prestanda

Om vi noggrant plottar in frekvensresponsen för filtret som vi konstruerade tidigare i artikeln, kommer vi att se att magnitudenresponsen vid 5 kHz i stort sett är 0 dB (dvs, nästan noll dämpning) och storleksresponsen vid 500 kHz är ungefär -14 dB (vilket motsvarar en förstärkning på 0,2). Dessa värden stämmer överens med resultaten av de beräkningar som vi utförde i föregående avsnitt.

Eftersom RC-filter alltid har en gradvis övergång från passband till stoppband, och eftersom dämpningen aldrig når oändligheten, kan vi inte konstruera ett ”perfekt” filter – det vill säga ett filter som inte har någon effekt på sinusvågen och som helt eliminerar bruset. Istället har vi alltid en kompromiss. Om vi flyttar gränsfrekvensen närmare 5 kHz får vi mer brusdämpning men också mer dämpning av den sinusvåg som vi vill skicka till en högtalare. Om vi flyttar avgränsningsfrekvensen närmare 500 kHz får vi mindre dämpning vid sinusvågsfrekvensen, men också mindre dämpning vid brusfrekvensen.

Lågpassfilterets fasförskjutning

Sedan tidigare har vi diskuterat hur ett filter ändrar amplituden för de olika frekvenskomponenterna i en signal. Reaktiva kretselement introducerar dock alltid fasförskjutning utöver amplitudeffekter.

Begreppet fas hänvisar till värdet av en periodisk signal vid en specifik tidpunkt inom en cykel. När vi säger att en krets orsakar fasförskjutning menar vi alltså att den skapar en felställning mellan ingångssignalen och utgångssignalen: ingångs- och utgångssignalerna börjar och slutar inte längre sina cykler vid samma tidpunkt. Fasförskjutningsvärdet, t.ex. 45° eller 90°, anger hur mycket feljustering som har skapats.

Varje reaktivt element i en krets medför 90° fasförskjutning, men denna fasförskjutning sker inte på en gång. Utgångssignalens fas, precis som utgångssignalens magnitud, ändras gradvis när ingångsfrekvensen ökar. I ett RC-lågpassfilter har vi ett reaktivt element (kondensatorn), och följaktligen kommer kretsen så småningom att introducera 90° fasförskjutning.

Som för storleksresponsen är fasresponsen lättast att utvärdera genom att undersöka en plott där den horisontella axeln anger logaritmisk frekvens. Beskrivningen nedan förmedlar det allmänna mönstret, och sedan kan du fylla i detaljerna genom att undersöka diagrammet.

Fasförskjutningen är inledningsvis 0°.
Den ökar gradvis tills den når 45° vid gränsfrekvensen; under denna del av responsen är förändringshastigheten ökande.
Efter gränsfrekvensen fortsätter fasförskjutningen att öka, men förändringshastigheten minskar.
Fasförskjutningen blir mycket liten när fasförskjutningen asymptotiskt närmar sig 90°.

Den heldragna linjen är magnituderesponsen och den streckade linjen är fassponsen. Brytningsfrekvensen är 100 kHz. Observera att fasförskjutningen är 45° vid gränsfrekvensen.

Sekunda ordningens lågpassfilter

Här långt har vi antagit att ett RC-lågpassfilter består av ett motstånd och en kondensator. Denna konfiguration är ett filter av första ordningen.

Den ”ordning” som ett passivt filter har bestäms av antalet reaktiva element – dvs. kondensatorer eller induktorer – som finns i kretsen. Ett filter av högre ordning har fler reaktiva element, vilket leder till större fasförskjutning och brantare avklingning. Denna andra egenskap är det främsta motivet för att öka ordningen på ett filter.

Om man lägger till ett reaktivt element till ett filter – t.ex. genom att gå från första ordningen till andra ordningen eller från andra ordningen till tredje ordningen – ökar vi den maximala roll-off med 20 dB/decad. Brantare roll-off översätts till en snabbare övergång från låg dämpning till hög dämpning, och detta kan leda till bättre prestanda när signalen inte har ett brett frekvensband som skiljer de önskade frekvenskomponenterna från bruskomponenterna.

Sekundordningsfilter byggs vanligen upp kring en resonanskrets som består av en induktor och en kondensator (denna topologi kallas ”RLC” för resistor-induktor-kondensator). Det är dock också möjligt att skapa RC-filter av andra ordningen. Som visas i diagrammet nedan behöver vi bara kaskadera två RC-filter av första ordningen.

Tyvärr skapar den här topologin visserligen en respons av andra ordningen, men den används inte i stor utsträckning – som vi kommer att se i nästa avsnitt är frekvensresponsen ofta sämre än hos ett aktivt filter av andra ordningen eller ett RLC-filter av andra ordningen.

Frekvensrespons för RC-filter av andra ordningen

Vi kan försöka skapa ett RC-lågpassfilter av andra ordningen genom att konstruera ett filter av första ordningen i enlighet med den önskade avgränsningsfrekvensen och sedan koppla två av dessa steg av första ordningen i serie. Detta resulterar visserligen i ett filter som har ett liknande övergripande frekvensomfång och en maximal roll-off på 40 dB/decad i stället för 20 dB/decad.

Och om vi tittar närmare på svaret ser vi att -3 dB-frekvensen har sjunkit. RC-filtret av andra ordningen beter sig inte som förväntat eftersom de två stegen inte är oberoende – vi kan inte helt enkelt koppla ihop dessa två steg och analysera kretsen som ett lågpassfilter av första ordningen följt av ett identiskt lågpassfilter av första ordningen.

För övrigt kommer dämpningen vid den ursprungliga cutoff-frekvensen att vara 6 dB i stället för 3 dB, även om vi sätter in en buffert mellan de två stegen, så att det första RC-steget och det andra RC-steget kan fungera som oberoende filter. Detta beror just på att de två stegen fungerar oberoende av varandra – det första filtret har 3 dB dämpning vid gränsfrekvensen och det andra filtret lägger till ytterligare 3 dB dämpning.

Den grundläggande begränsningen för det andra ordningens RC-lågpassfilter är att konstruktören inte kan finjustera övergången mellan genomströmningsband och stoppband genom att justera filtrets Q-faktor; denna parameter anger hur dämpad frekvensgången är. Om du kaskadkopplar två identiska RC-lågpassfilter motsvarar den totala överföringsfunktionen ett andra ordningens svar, men Q-faktorn är alltid 0,5. När Q = 0,5 är filtret på gränsen till överdämpat, och detta resulterar i ett frekvenssvar som ”hänger” i övergångsområdet. Andra ordningens aktiva filter och andra ordningens resonansbaserade filter har inte denna begränsning; konstruktören kan styra Q-faktorn och därmed finjustera frekvensresponsen i övergångsregionen.

Sammanfattning

Alla elektriska signaler innehåller en blandning av önskade frekvenskomponenter och oönskade frekvenskomponenter. De oönskade frekvenskomponenterna orsakas vanligtvis av brus och störningar, och i vissa situationer påverkar de systemets prestanda negativt.
Ett filter är en krets som reagerar på olika sätt på olika delar av en signals spektrum. Ett lågpassfilter är konstruerat för att släppa igenom lågfrekventa komponenter och blockera högfrekventa komponenter.
Gränsfrekvensen för ett lågpassfilter anger det frekvensområde där filtret övergår från låg dämpning till betydande dämpning.
Utgångsspänningen för ett RC-lågpassfilter kan beräknas genom att behandla kretsen som en spänningsdelare bestående av ett (frekvensoberoende) motstånd och en (frekvensberoende) reaktans.
En plott av magnituden (i dB, på den vertikala axeln) mot den logaritmiska frekvensen (i hertz, på den horisontella axeln) är ett bekvämt och effektivt sätt att undersöka det teoretiska beteendet hos ett filter. Du kan också använda en plott av fas mot logaritmisk frekvens för att bestämma storleken på den fasförskjutning som ska tillämpas på en insignal.
Ett filter av andra ordningen ger en brantare roll-off; detta svar av andra ordningen är användbart när en signal inte ger ett brett band av separation mellan önskade frekvenskomponenter och oönskade frekvenskomponenter.
Du kan skapa ett RC-lägpassfilter av andra ordningen genom att bygga två identiska RC-lägpassfilter av första ordningen och sedan ansluta utgången från det ena till ingången från det andra. Den totala -3 dB-frekvensen kommer att vara lägre än förväntat.