Vad är kärnan för trick? Varför är det viktigt?
När man talar om kärnor inom maskininlärning är det första man kommer att tänka på stödvektormodellen (SVM), eftersom kärntricket används ofta i SVM-modellen för att överbrygga linjäritet och icke-linjäritet.
För att hjälpa dig att förstå vad en kärna är och varför den är viktig kommer jag först att presentera grunderna i SVM-modellen.
SVM-modellen är en övervakad maskininlärningsmodell som främst används för klassificeringar (men den kan också användas för regression!). Den lär sig att separera olika grupper genom att bilda beslutsgränser. De blå punkterna och de lila punkterna. Det finns massor av sätt att separera dessa två klasser, vilket visas i grafen till vänster. Vi vill dock hitta det ”bästa” hyperplanet som kan maximera marginalen mellan dessa två klasser, vilket innebär att avståndet mellan hyperplanet och de närmaste datapunkterna på vardera sidan är störst. Beroende på vilken sida av hyperplanet en ny datapunkt befinner sig på kan vi tilldela den nya observationen en klass.
Det låter enkelt i exemplet ovan. Alla data är dock inte linjärt separerbara. I verkligheten är faktiskt nästan alla data slumpmässigt fördelade, vilket gör det svårt att separera olika klasser linjärt.


Varför är det viktigt att använda kärntricket?
Som du kan se i bilden ovan kan vi, om vi hittar ett sätt att kartlägga data från ett tvådimensionellt rum till ett tredimensionellt rum, hitta en beslutsyta som tydligt skiljer mellan olika klasser. Min första tanke med denna datatransformationsprocess är att kartlägga alla datapunkter till en högre dimension (i det här fallet 3-dimensionell), hitta gränsen och göra en klassificering.
Det låter bra. Men när det finns fler och fler dimensioner blir beräkningarna inom det utrymmet allt dyrare. Det är då som kärntricket kommer in i bilden. Det gör det möjligt för oss att operera i det ursprungliga funktionsutrymmet utan att beräkna koordinaterna för uppgifterna i ett högre dimensionellt utrymme.
Låt oss titta på ett exempel:
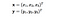

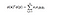
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
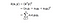
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Alla beräkningar som involverar punktprodukterna (x, y) kan använda sig av kärntricket.
Differenta kärnfunktioner
Det finns olika kärnor. De mest populära är polynomkärnan och RBF-kärnan (radiell basfunktion).
”Intuitivt sett tittar polynomkärnan inte bara på de givna egenskaperna hos de ingående proverna för att bestämma deras likhet, utan även på kombinationer av dessa” (Wikipedia), precis som exemplet ovan. Med n ursprungliga egenskaper och d grader av polynom ger polynomkärnan n^d expanderade egenskaper.
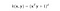
RBF-kärnan kallas också för Gauss-kärnan. Det finns ett oändligt antal dimensioner i funktionsutrymmet eftersom det kan expanderas med Taylor-serien. I formatet nedan definierar parametern γ hur stort inflytande ett enskilt träningsexempel har. Ju större den är, desto närmare måste andra exempel ligga för att påverkas (sklearn-dokumentation).
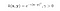
Det finns olika alternativ för kärnfunktionerna i biblioteket sklearn i Python. Du kan till och med bygga en anpassad kärna om det behövs.
Slutet
Kärntricket låter som en ”perfekt” plan. En kritisk sak att tänka på är dock att när vi mappar data till en högre dimension finns det risk för att vi överanpassar modellen. Därför är det av stor vikt att välja rätt kärnfunktion (inklusive rätt parametrar) och regularisering.
Om du är nyfiken på vad regularisering är har jag skrivit en artikel där jag talar om min förståelse av det och du hittar den här.
Jag hoppas att du tycker om den här artikeln. Som alltid är du välkommen att höra av dig till mig om du har några frågor, kommentarer, förslag osv. Tack för att du läste 🙂