Wat is de kerneltruc? Waarom is het belangrijk?
Als we het hebben over kernels in machine learning, is het eerste wat in je opkomt waarschijnlijk het support vector machines (SVM) model, omdat de kernel truc veel wordt gebruikt in het SVM model om lineariteit en niet-lineariteit te overbruggen.
Om je te helpen begrijpen wat een kernel is en waarom die belangrijk is, zal ik eerst de basis van het SVM-model introduceren.
Het SVM-model is een machine-learning model dat vooral voor classificaties wordt gebruikt (maar het kan ook voor regressie worden gebruikt!). Het leert hoe het verschillende groepen kan scheiden door beslissingsgrenzen te vormen.

In de bovenstaande grafiek zien we dat er twee klassen van waarnemingen zijn: de blauwe punten en de paarse punten. Er zijn talloze manieren om deze twee klassen te scheiden, zoals de grafiek links laat zien. We willen echter het “beste” hypervlak vinden dat de marge tussen deze twee klassen kan maximaliseren, wat betekent dat de afstand tussen het hypervlak en de dichtstbijzijnde datapunten aan elke kant het grootst is. Afhankelijk van aan welke kant van het hypervlak een nieuw gegevenspunt ligt, kunnen we aan de nieuwe waarneming een klasse toekennen.
Het klinkt eenvoudig in het bovenstaande voorbeeld. Niet alle gegevens zijn echter lineair scheidbaar. In de echte wereld zijn bijna alle gegevens willekeurig verdeeld, waardoor het moeilijk is de verschillende klassen lineair te scheiden.

Waarom is het belangrijk om de kerneltruc te gebruiken?
Zoals u in de bovenstaande afbeelding kunt zien, kunnen we, als we een manier vinden om de gegevens van een 2-dimensionale ruimte naar een 3-dimensionale ruimte te mappen, een beslissingsoppervlak vinden dat duidelijk onderscheid maakt tussen verschillende klassen. Mijn eerste gedachte bij dit datatransformatieproces is om alle datapunten naar een hogere dimensie (in dit geval, 3-dimensie) te mappen, de grens te vinden, en de classificatie te maken.
Dat klinkt goed. Maar als er meer en meer dimensies zijn, worden de berekeningen binnen die ruimte steeds duurder. En dan komt de kernel-truc om de hoek kijken. Hiermee kunnen we werken in de oorspronkelijke ruimte zonder de coördinaten van de gegevens te berekenen in een ruimte met hogere dimensies.
Laten we eens naar een voorbeeld kijken:
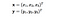
Hier zijn x en y twee datapunten in 3 dimensies. Laten we aannemen dat we x en y moeten toewijzen aan een 9-dimensionale ruimte. We moeten de volgende berekeningen uitvoeren om het eindresultaat te krijgen, dat slechts een scalair is. De rekenkundige complexiteit is in dit geval O(n²).

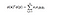
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
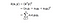
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Bij alle berekeningen waarbij de puntproducten (x, y) een rol spelen, kan de kerneltruc worden toegepast.
Verschillende kernelfuncties
Er zijn verschillende kernels. De meest populaire zijn de polynomiale kernel en de radiale basisfunctie (RBF) kernel.
“Intuïtief kijkt de polynomiale kernel niet alleen naar de gegeven kenmerken van invoermonsters om hun overeenkomst te bepalen, maar ook naar combinaties daarvan” (Wikipedia), net als in het voorbeeld hierboven. Met n originele kenmerken en d polynomiale graden, levert de polynomiale kernel n^d uitgebreide kenmerken op.
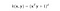
De RBF-kernel wordt ook wel de Gaussiaanse kernel genoemd. Er is een oneindig aantal dimensies in de feature space omdat deze kan worden uitgebreid met de Taylor Series. In de onderstaande indeling bepaalt de parameter γ hoeveel invloed een enkel trainingsvoorbeeld heeft. Hoe groter deze is, hoe dichter andere voorbeelden moeten zijn om te worden beïnvloed (sklearn documentatie).
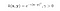
Er zijn verschillende opties voor de kernelfuncties in de sklearn-bibliotheek in Python. Je kunt zelfs een eigen kernel bouwen als dat nodig is.
Het einde
De kerneltruc klinkt als een “perfect” plan. Een belangrijk punt om in gedachten te houden is echter dat wanneer we gegevens in een hogere dimensie plaatsen, de kans bestaat dat we het model overfitten. Daarom zijn de keuze van de juiste kernelfunctie (inclusief de juiste parameters) en regularisatie van groot belang.
Als je nieuwsgierig bent naar wat regularisatie is, heb ik een artikel geschreven over wat ik ervan versta en dat kun je hier vinden.
Ik hoop dat je dit artikel leuk vindt. Laat het me zoals altijd weten als je vragen, opmerkingen, suggesties, enz. hebt. Bedankt voor het lezen 🙂