O que é um Filtro Passa-baixo? Um Tutorial sobre o Básico de Filtros Passivos de RC

Dezembro 5, 2021admin

O que é filtragem? Aprenda o que são filtros passa-baixo resistor (RC) e onde pode utilizá-los.

Este artigo introduz o conceito de filtragem e explica em detalhe a finalidade e características dos filtros passa-baixo resistor (RC).

Domínio de Tempo e Domínio de Frequência

Quando você olha para um sinal elétrico em um osciloscópio, você vê uma linha que representa mudanças de voltagem em relação ao tempo. Em qualquer momento específico no tempo, o sinal tem apenas um valor de voltagem. O que você vê no osciloscópio é a representação de domínio de tempo do sinal.

Um traço típico do osciloscópio é simples e intuitivo, mas também é um pouco restritivo, porque não revela diretamente o conteúdo de freqüência de um sinal. Ao contrário da representação do domínio do tempo, em que um momento no tempo corresponde apenas a um valor de tensão, uma representação do domínio de frequência (também chamada espectro) transmite informação sobre um sinal identificando os vários componentes de frequência que estão simultaneamente presentes.

Representações do domínio temporal de uma sinusoidal (topo) e de uma onda quadrada (fundo).

Representações de domínio de frequência de um sinusoidal (topo) e de uma onda quadrada (fundo).

O que é um filtro?

Um filtro é um circuito que remove, ou “filtra para fora”, uma gama específica de componentes de frequência. Em outras palavras, ele separa o espectro do sinal em componentes de freqüência que serão passados e componentes de freqüência que serão bloqueados.

Se você não tem muita experiência com análise de domínio de freqüência, você ainda pode ter dúvidas sobre o que são esses componentes de freqüência e como eles coexistem em um sinal que não pode ter múltiplos valores de tensão ao mesmo tempo. Vamos ver um breve exemplo que ajudará a esclarecer este conceito.

Vamos imaginar que temos um sinal de áudio que consiste numa onda senoidal perfeita de 5 kHz. Sabemos como é uma onda senoidal no domínio do tempo, e no domínio da frequência não veremos nada mais que um “pico” de frequência a 5 kHz. Agora vamos supor que ativamos um oscilador de 500 kHz que introduz ruído de alta freqüência no sinal de áudio.

O sinal como visto em um osciloscópio ainda será apenas uma seqüência de tensões, com um valor por momento de tempo, mas o sinal terá um aspecto diferente porque suas variações no domínio do tempo devem agora refletir tanto a onda senoidal de 5 kHz quanto as flutuações do ruído de alta freqüência.

No domínio da freqüência, no entanto, a onda senoidal e o ruído são componentes de freqüência separados que estão presentes simultaneamente neste único sinal. A onda senoidal e o ruído ocupam diferentes porções da representação de domínio de freqüência do sinal (como mostrado no diagrama abaixo), e isto significa que podemos filtrar o ruído dirigindo o sinal através de um circuito que passa por freqüências baixas e bloqueia freqüências altas.

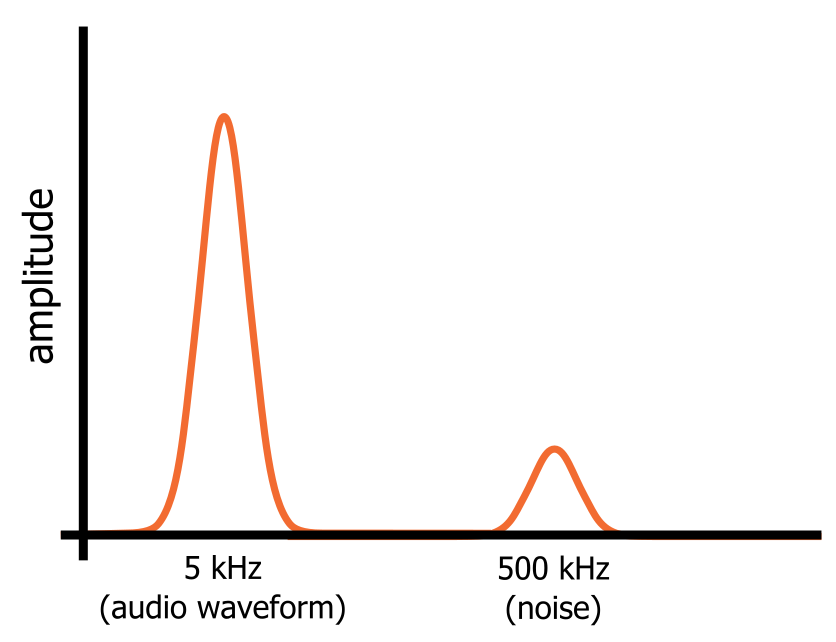
Tipos de Filtros

Filtros podem ser colocados em categorias amplas que correspondem às características gerais da resposta de freqüência do filtro. Se um filtro passa por freqüências baixas e bloqueia freqüências altas, ele é chamado de filtro passa-baixo. Se ele bloqueia frequências baixas e passa frequências altas, é um filtro passa-alto. Existem também filtros passa-banda, que passam apenas uma gama relativamente estreita de frequências, e filtros pára-banda, que bloqueiam apenas uma gama relativamente estreita de frequências.

Filtros também podem ser classificados de acordo com os tipos de componentes que são utilizados para implementar o circuito. Os filtros passivos utilizam resistências, condensadores e indutores; estes componentes não têm a capacidade de fornecer amplificação e, consequentemente, um filtro passivo só pode manter ou reduzir a amplitude de um sinal de entrada. Um filtro ativo, por outro lado, pode tanto filtrar um sinal quanto aplicar ganho, pois inclui um componente ativo como um transistor ou um amplificador operacional.

Este filtro passa-baixo ativo é baseado na popular topologia Sallen-Key.

Este artigo explora a análise e o projeto de filtros passa-baixo passivos. Estes circuitos desempenham um papel importante numa grande variedade de sistemas e aplicações.

O filtro passa-baixo RC

Para criar um filtro passa-baixo passivo, precisamos de combinar um elemento resistivo com um elemento reactivo. Em outras palavras, precisamos de um circuito que consiste de uma resistência e um condensador ou um indutor. Em teoria, a topologia do resistor-indutor (RL) passa-baixo é equivalente, em termos de capacidade de filtragem, à topologia do resistor-capacitor (RC) passa-baixo. Na prática, porém, a versão resistor-capacitor é muito mais comum, e consequentemente o resto deste artigo irá focar no filtro passa-baixo RC.

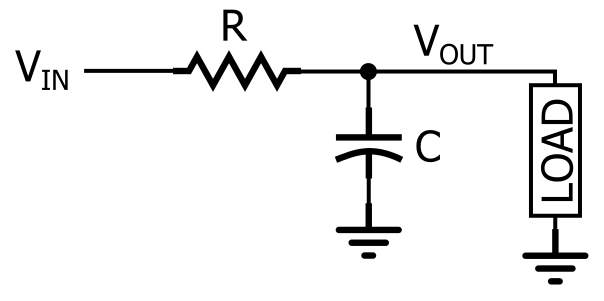
O filtro passa-baixo RC.

Como pode ver no diagrama, uma resposta passa-baixo RC é criada colocando um resistor em série com o caminho do sinal e um condensador em paralelo com a carga. No diagrama, a carga é um componente único, mas em um circuito real pode ser algo muito mais complicado, como um conversor analógico-digital, um amplificador ou o estágio de entrada do osciloscópio que você está usando para medir a resposta do filtro.

Podemos analisar intuitivamente a ação de filtragem da topologia RC passa-baixo se reconhecermos que o resistor e o capacitor formam um divisor de tensão dependente da freqüência.

O filtro RC passa-baixo redesenhado de forma a parecer um divisor de tensão.

Quando a frequência do sinal de entrada é baixa, a impedância do condensador é alta em relação à impedância da resistência; assim, a maior parte da tensão de entrada é baixada através do condensador (e através da carga, que está em paralelo com o condensador). Quando a freqüência de entrada é alta, a impedância do capacitor é baixa em relação à impedância da resistência, o que significa que mais voltagem é descartada através da resistência e menos é transferida para a carga. Assim, as baixas frequências são passadas e as altas frequências são bloqueadas.

Esta explicação qualitativa da funcionalidade RC low-pass é um primeiro passo importante, mas não é muito útil quando precisamos realmente projetar um circuito, porque os termos “alta frequência” e “baixa frequência” são extremamente vagos. Os engenheiros precisam de criar circuitos que passem e bloqueiem frequências específicas. Por exemplo, no sistema de áudio descrito acima, queremos preservar um sinal de 5 kHz e suprimir um sinal de 500 kHz. Isto significa que precisamos de um filtro que passe para o bloqueio entre 5 kHz e 500 kHz.

A Frequência de Corte

A gama de frequências para as quais um filtro não causa atenuação significativa é chamada de banda passante, e a gama de frequências para as quais o filtro causa atenuação significativa é chamada de banda de paragem. Os filtros analógicos, como o filtro RC de baixa passagem, sempre transitam gradualmente da banda passante para a banda de parada. Isto significa que é impossível identificar uma freqüência na qual o filtro pára de passar sinais e começa a bloquear os sinais. No entanto, os engenheiros precisam de uma maneira conveniente e concisa de resumir a resposta de frequência de um filtro, e é aqui que entra em jogo o conceito de frequência de corte.

Quando você olha para um gráfico da resposta de frequência de um filtro RC, você vai notar que o termo “frequência de corte” não é muito preciso. A imagem do espectro de um sinal sendo “cortado” em duas metades, uma das quais é retida e a outra é descartada, não se aplica, porque a atenuação aumenta gradualmente à medida que as frequências se movem de abaixo do corte para acima do corte.

A frequência de corte de um filtro RC de baixa passagem é na verdade a frequência em que a amplitude do sinal de entrada é reduzida em 3 dB (este valor foi escolhido porque uma redução de 3 dB na amplitude corresponde a uma redução de 50% na potência). Assim, a frequência de corte também é chamada de frequência de -3 dB, e na verdade este nome é mais preciso e mais informativo. O termo largura de banda refere-se à largura da banda passante de um filtro, e no caso de um filtro passa-baixo, a largura de banda é igual à frequência de -3 dB (como mostrado no diagrama abaixo).

Este diagrama transmite as características genéricas da resposta de frequência de um filtro passa-baixo RC. A largura de banda é igual à frequência de -3 dB.

Como explicado acima, o comportamento de baixa passagem de um filtro RC é causado pela interação entre a impedância independente da frequência do resistor e a impedância dependente da frequência do condensador. Para determinar os detalhes da resposta em freqüência de um filtro, precisamos analisar matematicamente a relação entre resistência (R) e capacitância (C), e também podemos manipular esses valores para projetar um filtro que atenda a especificações precisas. A frequência de corte (fC) de um filtro RC de baixa passagem é calculada da seguinte forma:

Vejamos um exemplo de desenho simples. Os valores dos condensadores são mais restritivos que os valores das resistências, por isso vamos começar com um valor comum de capacitância (como 10 nF), e depois vamos usar a equação para determinar o valor de resistência requerido. O objetivo é projetar um filtro que irá preservar uma forma de onda de áudio de 5 kHz e rejeitar uma forma de onda de ruído de 500 kHz. Vamos tentar uma frequência de corte de 100 kHz, e mais tarde no artigo vamos analisar mais cuidadosamente o efeito deste filtro nos dois componentes de frequência.

Thus, um resistor de 160 Ω combinado com um condensador de 10 nF dar-nos-á um filtro que se aproxima muito da resposta de frequência desejada.

Cálculo da resposta do filtro

Podemos calcular o comportamento teórico de um filtro passa-baixo usando uma versão dependente da frequência de um cálculo típico de divisor de tensão. A saída de um divisor de tensão resistivo é expressa da seguinte forma:

O filtro RC utiliza uma estrutura equivalente, mas em vez de R2 temos um condensador. Primeiro, substituímos R2 (no numerador) pela reactância do condensador (XC). Em seguida, precisamos calcular a magnitude da impedância total e colocá-la no denominador. Assim, temos

A reactância de um condensador indica a quantidade de oposição ao fluxo de corrente, mas ao contrário da resistência, a quantidade de oposição depende da frequência do sinal que passa através do condensador. Assim, temos que calcular a reactância a uma frequência específica, e a equação que usamos para isso é a seguinte:

No exemplo de desenho acima, R ≈ 160 Ω e C = 10 nF. Vamos assumir que a amplitude do VIN é 1 V, de modo que podemos simplesmente remover o VIN do cálculo. Primeiro vamos calcular a amplitude do VOUT na freqüência da onda sinusoidal:

A amplitude da onda sinusoidal é essencialmente inalterada. Isso é bom, já que nossa intenção era preservar a onda sinusoidal enquanto suprimíamos o ruído. Este resultado não é surpreendente, já que escolhemos uma frequência de corte (100 kHz) que é muito superior à frequência da onda sinusoidal (5 kHz).

Agora vamos ver como o filtro vai atenuar com sucesso a componente de ruído.

A amplitude do ruído é apenas cerca de 20% do seu valor original.

Visualização da resposta do filtro

O meio mais conveniente de avaliar o efeito de um filtro sobre um sinal é examinar um gráfico da resposta de frequência do filtro. Estes gráficos, frequentemente chamados gráficos de Bode, têm magnitude (em decibéis) no eixo vertical e frequência no eixo horizontal; o eixo horizontal tem tipicamente uma escala logarítmica, tal que a distância física entre 1 Hz e 10 Hz é a mesma que a distância física entre 10 Hz e 100 Hz, entre 100 Hz e 1 kHz, e assim por diante. Esta configuração permite-nos avaliar de forma rápida e precisa o comportamento de um filtro numa gama muito grande de frequências.

Um exemplo de gráfico de frequência-resposta.

Cada ponto da curva indica a magnitude que o sinal de saída terá se o sinal de entrada tiver uma magnitude de 1 V e uma frequência igual ao valor correspondente no eixo horizontal. Por exemplo, quando a freqüência de entrada é 1 MHz, a amplitude de saída (assumindo uma amplitude de entrada de 1 V) será de 0,1 V (porque -20 dB corresponde a um fator de redução de dez).

A forma geral desta curva freqüência-resposta se tornará muito familiar à medida que você gastar mais tempo com circuitos de filtragem. A curva é quase perfeitamente plana na banda passante, e depois começa a cair mais rapidamente à medida que a frequência de entrada se aproxima da frequência de corte. Eventualmente, a taxa de mudança na atenuação, chamada de roll-off, estabiliza-se em 20 dB/decada- isto é, a magnitude do sinal de saída é reduzida em 20 dB para cada fator de dez aumentos na freqüência de entrada.

Assessing Low-Pass Filter Performance

Se traçarmos cuidadosamente a resposta de freqüência do filtro que projetamos anteriormente no artigo, veremos que a resposta de magnitude a 5 kHz é essencialmente 0 dB (ou seja atenuação quase zero) e a resposta de magnitude a 500 kHz é aproximadamente -14 dB (o que corresponde a um ganho de 0,2). Estes valores são consistentes com os resultados dos cálculos que fizemos na secção anterior.

Porque os filtros RC têm sempre uma transição gradual da banda passante para a banda parada, e porque a atenuação nunca chega ao infinito, não podemos conceber um filtro “perfeito” – isto é, um filtro que não tem efeito sobre a onda sinusoidal e elimina completamente o ruído. Em vez disso, temos sempre um trade-off. Se movermos a frequência de corte para mais perto de 5 kHz, teremos mais atenuação do ruído, mas também mais atenuação da onda sinusoidal que queremos enviar a um altifalante. Se movermos a frequência de corte para mais perto de 500 kHz, teremos menos atenuação na frequência da onda sinusoidal, mas também menos atenuação na frequência do ruído.

Low-Pass Filter Phase Shift

Até agora discutimos a forma como um filtro modifica a amplitude dos vários componentes de frequência num sinal. No entanto, elementos de circuito reativos sempre introduzem o deslocamento de fase além dos efeitos de amplitude.

O conceito de fase refere-se ao valor de um sinal periódico em um momento específico dentro de um ciclo. Assim, quando dizemos que um circuito causa uma mudança de fase, queremos dizer que ele cria um desalinhamento entre o sinal de entrada e o sinal de saída: os sinais de entrada e saída não começam e terminam mais seus ciclos no mesmo momento no tempo. O valor do deslocamento de fase, como 45° ou 90°, indica quanto desalinhamento foi criado.

Cada elemento reativo em um circuito introduz 90° de deslocamento de fase, mas este deslocamento de fase não acontece de uma só vez. A fase do sinal de saída, tal como a magnitude do sinal de saída, muda gradualmente à medida que a frequência de entrada aumenta. Em um filtro RC de baixa passagem, temos um elemento reativo (o condensador), e conseqüentemente o circuito eventualmente introduzirá 90° de deslocamento de fase.

As com resposta de magnitude, a resposta de fase é mais facilmente avaliada pelo exame de um gráfico no qual o eixo horizontal indica a freqüência logarítmica. A descrição abaixo transmite o padrão geral, e então você pode preencher os detalhes examinando o gráfico.

Deslocamento de fase é inicialmente 0°.
Aumenta gradualmente até atingir 45° na freqüência de corte; durante esta parte da resposta, a taxa de mudança está aumentando.
Após a freqüência de corte, o deslocamento de fase continua a aumentar, mas a taxa de mudança está diminuindo.
A taxa de mudança torna-se muito pequena à medida que o deslocamento de fase se aproxima assimetricamente de 90°.

A linha sólida é a resposta de magnitude, e a linha pontilhada é a resposta de fase. A frequência de corte é de 100 kHz. Note que o deslocamento de fase é de 45° na frequência de corte.

Second-Order Low-Pass Filters

Até agora assumimos que um filtro RC low-pass consiste de uma resistência e um condensador. Esta configuração é um filtro de primeira ordem.

A “ordem” de um filtro passivo é determinada pelo número de elementos reactivos – ou seja, condensadores ou indutores – que estão presentes no circuito. Um filtro de ordem superior tem mais elementos reativos, o que leva a mais deslocamento de fase e a um roll-off mais acentuado. Esta segunda característica é a principal motivação para aumentar a ordem de um filtro.

Adicionando um elemento reativo a um filtro – por exemplo, passando da primeira ordem para a segunda ou segunda ordem para a terceira – aumentamos o roll-off máximo em 20 dB/década. O roll-off mais acentuado traduz-se numa transição mais rápida de baixa atenuação para alta atenuação, e isto pode resultar num melhor desempenho quando o sinal não tem uma banda de frequência larga que separa os componentes de frequência desejados dos componentes de ruído.

Filtros de segunda ordem são normalmente construídos em torno de um circuito ressonante composto por um indutor e um condensador (esta topologia é chamada de “RLC” para resistor-indutor-capacitor). No entanto, também é possível criar filtros RC de segunda ordem. Como mostrado no diagrama abaixo, tudo o que precisamos fazer é criar dois filtros RC de primeira ordem em cascata.

p> Posto que esta topologia certamente cria uma resposta de segunda ordem, ela não é amplamente utilizada – como veremos na próxima seção, a resposta de freqüência é frequentemente inferior à de um filtro ativo de segunda ordem ou de um filtro RLC de segunda ordem.

Frequency Response of the Second-Order RC Filter

Podemos tentar criar um filtro passa-baixo RC de segunda ordem desenhando um filtro de primeira ordem de acordo com a frequência de corte desejada e depois conectando dois desses estágios de primeira ordem em série. Isto resulta num filtro que tem uma resposta de frequência geral semelhante e um roll-off máximo de 40 dB/década em vez de 20 dB/década.

No entanto, se olharmos para a resposta mais de perto, vemos que a frequência de -3 dB diminuiu. O filtro RC de segunda ordem não se comporta como esperado porque os dois estágios não são independentes – não podemos simplesmente conectar esses dois estágios juntos e analisar o circuito como um filtro passa-baixo de primeira ordem seguido por um filtro passa-baixo de primeira ordem idêntico.

Outras vezes, mesmo se inserirmos um buffer entre os dois estágios, para que o primeiro estágio RC e o segundo estágio RC possam funcionar como filtros independentes, a atenuação na freqüência de corte original será de 6 dB ao invés de 3 dB. Isto ocorre precisamente porque os dois estágios estão operando independentemente – o primeiro filtro tem 3 dB de atenuação na freqüência de corte, e o segundo filtro adiciona outros 3 dB de atenuação.

A limitação fundamental do filtro passa-baixo RC de segunda ordem é que o projetista não pode afinar a transição da banda passante para a banda parada ajustando o fator Q do filtro; este parâmetro indica o quão amortecida é a resposta de freqüência. Se você colocar em cascata dois filtros passa-baixo RC idênticos, a função de transferência geral corresponde a uma resposta de segunda ordem, mas o fator Q é sempre 0,5. Quando Q = 0,5, o filtro está na borda de ser sobre-amortecido, e isto resulta numa resposta de frequência que “desce” na região de transição. Filtros ativos de segunda ordem e filtros baseados em ressonância de segunda ordem não têm essa limitação; o projetista pode controlar o fator Q e assim ajustar a resposta de freqüência na região de transição.

Sumário

Todos os sinais elétricos contêm uma mistura de componentes de freqüência desejados e componentes de freqüência indesejados. Os componentes de freqüência indesejados são tipicamente causados por ruído e interferência, e em algumas situações eles irão afetar negativamente o desempenho do sistema.
Um filtro é um circuito que reage de diferentes maneiras a diferentes porções do espectro de um sinal. Um filtro passa-baixo é projetado para passar componentes de baixa freqüência e bloquear componentes de alta freqüência.
A freqüência de corte de um filtro passa-baixo indica a região de freqüência na qual o filtro está fazendo a transição de baixa atenuação para atenuação significativa.
A tensão de saída de um filtro passa-baixo RC pode ser calculada tratando o circuito como um divisor de tensão constituído por uma resistência (independente da frequência) e uma reactância (dependente da frequência).
Um gráfico de magnitude (em dB, no eixo vertical) versus frequência logarítmica (em hertz, no eixo horizontal) é uma forma conveniente e eficaz de examinar o comportamento teórico de um filtro. Você também pode usar um gráfico de fase versus freqüência logarítmica para determinar a quantidade de deslocamento de fase que será aplicada a um sinal de entrada.
Um filtro de segunda ordem fornece um roll-off mais acentuado; esta resposta de segunda ordem é útil quando um sinal não fornece uma ampla faixa de separação entre componentes de freqüência desejados e componentes de freqüência indesejados.
Você pode criar um filtro passa-baixo RC de segunda ordem construindo dois filtros passa-baixo RC idênticos de primeira ordem e então conectando a saída de um à entrada do outro. A frequência global de -3 dB será inferior ao esperado.