10.13: Avogadrova hypotéza a molární objem

admin

Avogadrova hypotéza a molární objem

Objem je po počtu prvků a hmotnosti třetím způsobem měření množství látky. U kapalin a pevných látek se objem značně liší v závislosti na hustotě látky. Je to proto, že pevné a kapalné částice jsou namačkány těsně vedle sebe a mezi částicemi je jen velmi málo místa. Plyny jsou však z velké části tvořeny prázdnými prostory mezi vlastními částicemi plynu (viz obrázek níže).

Obrázek \(\PageIndex{1}\):

V roce 1811 Amadeo Avogadro vysvětlil, že objemy všech plynů lze snadno určit. Avogadrova hypotéza říká, že stejné objemy všech plynů při stejné teplotě a tlaku obsahují stejný počet částic. Protože celkový objem, který plyn zaujímá, je tvořen především prázdným prostorem mezi částicemi, je skutečná velikost samotných částic téměř zanedbatelná. Daný objem plynu s malými lehkými částicemi, jako je vodík, \(\left( \ce{H_2} \right)\) obsahuje stejný počet částic jako stejný objem těžkého plynu s velkými částicemi, jako je hexafluorid síry, \(\ce{SF_6}\).

Plyny jsou stlačitelné, což znamená, že jsou-li vystaveny vysokému tlaku, jsou částice tlačeny blíže k sobě. Tím se zmenšuje množství prázdného prostoru a zmenšuje se objem plynu. Objem plynu ovlivňuje také teplota. Když se plyn zahřívá, jeho molekuly se pohybují rychleji a plyn se rozpíná. Vzhledem ke změnám objemu plynu v důsledku změn tlaku a teploty je třeba porovnávat objemy plynů při jedné standardní teplotě a tlaku. Standardní teplota a tlak (STP) je definována jako \(0^\text{o} \text{C}\) \(\left( 273,15 \: \text{K} \right)\) a \(1 \: \text{atm}}) tlak. Molární objem plynu je objem jednoho molu plynu při STP. Při STP zaujímá jeden mol (\( 6,02 \krát 10^{23}\) reprezentativní částice) jakéhokoli plynu objem \(22,4 \: \text{L}\) (obrázek níže).

Obrázek \(\PageIndex{2}\): Jeden mol libovolného plynu zabírá \(22,4 \: \text{L}\) při standardní teplotě a tlaku (\(0^\text{o} \text{C}\) a \(1 \: \text{atm}\).

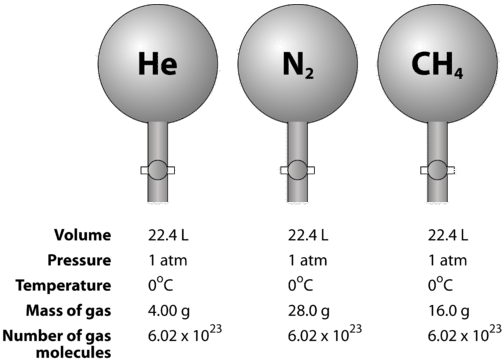
Následující obrázek znázorňuje, jak lze při porovnávání různých plynů vidět molární objem. Vzorky helia \(\left( \ce{He} \right)\), dusíku \(\left( \ce{N_2} \right)\) a metanu \(\left( \ce{CH_4} \right)\) jsou při STP. Každý z nich obsahuje 1 mol nebo \(6,02 \krát 10^{23}\) částic. Hmotnost každého plynu je však jiná a odpovídá molární hmotnosti tohoto plynu: \(4,00 \: \text{g/mol}\) pro \(\ce{He}\), \(28,0 \: \text{g/mol}\) pro \(\ce{N_2}\) a \(16,0 \: \text{g/mol}\) pro \(\ce{CH_4}\).

Obrázek \(\PageIndex{3}\): Avogadrova hypotéza říká, že stejné objemy jakéhokoli plynu při stejné teplotě a tlaku obsahují stejný počet částic. Při standardní teplotě a tlaku zaujímá 1 mol libovolného plynu \(22,4 \: \text{L}\).