Co je to filtr dolní propusti? Výukový program o základech pasivních RC filtrů

5 prosince, 2021admin

Co je to filtrace? Zjistěte, co jsou to nízkoprůchodové filtry s rezistorem a kondenzátorem (RC) a kde je můžete použít.

Tento článek seznamuje s pojmem filtrace a podrobně vysvětluje účel a vlastnosti nízkoprůchodových filtrů s rezistorem a kondenzátorem (RC).

Časová a frekvenční doména

Při pohledu na elektrický signál na osciloskopu vidíte čáru, která představuje změny napětí v závislosti na čase. V každém konkrétním časovém okamžiku má signál pouze jednu hodnotu napětí. To, co vidíte na osciloskopu, je reprezentace signálu v časové oblasti.

Typická stopa osciloskopu je přímočará a intuitivní, ale je také poněkud omezující, protože přímo neodhaluje frekvenční obsah signálu. Na rozdíl od reprezentace v časové oblasti, v níž jednomu časovému okamžiku odpovídá pouze jedna hodnota napětí, reprezentace ve frekvenční oblasti (nazývaná také spektrum) zprostředkovává informace o signálu identifikací různých frekvenčních složek, které jsou současně přítomny.

Zobrazení sinusoidy (nahoře) a čtvercové vlny (dole) v časové oblasti.

Zobrazení sinusoidy (nahoře) a čtvercové vlny (dole) ve frekvenční oblasti

Co je to filtr?

Filtr je obvod, který odstraňuje neboli „filtruje“ určitý rozsah frekvenčních složek. Jinými slovy, rozdělí spektrum signálu na frekvenční složky, které projdou, a frekvenční složky, které budou blokovány.

Pokud nemáte s analýzou ve frekvenční oblasti mnoho zkušeností, možná si stále nejste jisti, co jsou to frekvenční složky a jak koexistují v signálu, který nemůže mít více hodnot napětí současně. Podívejme se na krátký příklad, který nám pomůže tento pojem objasnit.

Představme si, že máme zvukový signál, který se skládá z dokonalé sinusovky o frekvenci 5 kHz. Víme, jak vypadá sinusovka v časové oblasti, a ve frekvenční oblasti neuvidíme nic jiného než frekvenční „hrot“ na 5 kHz. Nyní předpokládejme, že aktivujeme oscilátor s frekvencí 500 kHz, který do zvukového signálu vnese vysokofrekvenční šum.

Signál viditelný na osciloskopu bude stále tvořen pouze jednou posloupností napětí s jednou hodnotou v každém časovém okamžiku, ale signál bude vypadat jinak, protože jeho změny v časové oblasti nyní musí odrážet jak sinusovou vlnu 5 kHz, tak vysokofrekvenční kolísání šumu.

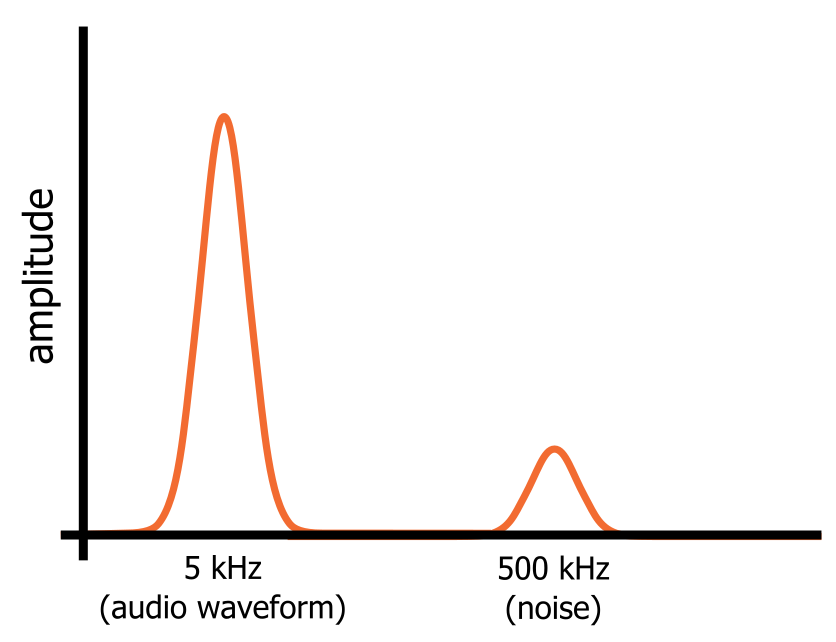
Ve frekvenční oblasti jsou však sinusová vlna a šum samostatné frekvenční složky, které jsou v tomto jednom signálu přítomny současně. Sinusovka a šum zabírají různé části reprezentace signálu ve frekvenční oblasti (jak je znázorněno na obrázku níže), a to znamená, že můžeme odfiltrovat šum tím, že signál nasměrujeme přes obvod, který propouští nízké frekvence a blokuje vysoké frekvence.

Typy filtrů

Filtry lze zařadit do širokých kategorií, které odpovídají obecným charakteristikám frekvenční charakteristiky filtru. Pokud filtr propouští nízké frekvence a blokuje vysoké frekvence, nazývá se dolnopropustný filtr. Pokud blokuje nízké frekvence a propouští vysoké frekvence, jedná se o vysokofrekvenční filtr. Existují také pásmové filtry, které propouštějí pouze relativně úzký rozsah frekvencí, a pásmové filtry, které blokují pouze relativně úzký rozsah frekvencí.

Filtry lze také klasifikovat podle typů součástek, které jsou použity k realizaci obvodu. Pasivní filtry používají rezistory, kondenzátory a cívky; tyto součástky nemají schopnost zajistit zesílení, a proto pasivní filtr může pouze zachovat nebo snížit amplitudu vstupního signálu. Aktivní filtr naproti tomu dokáže jak filtrovat signál, tak použít zesílení, protože obsahuje aktivní součástku, jako je tranzistor nebo operační zesilovač.

Tento aktivní filtr dolní propusti je založen na populární topologii Sallen-Key.

Tento článek se zabývá analýzou a návrhem pasivních filtrů dolní propusti. Tyto obvody hrají důležitou roli v nejrůznějších systémech a aplikacích.

RC dolnopropustný filtr

Pro vytvoření pasivního dolnopropustného filtru musíme zkombinovat odporový prvek s jalovým prvkem. Jinými slovy, potřebujeme obvod, který se skládá z rezistoru a kondenzátoru nebo induktoru. Teoreticky je topologie dolní propusti rezistor-induktor (RL) z hlediska filtrační schopnosti ekvivalentní topologii dolní propusti rezistor-kondenzátor (RC). V praxi se však mnohem častěji používá verze s rezistorem a kondenzátorem, a proto se ve zbytku tohoto článku zaměříme na nízkoprůchodový filtr RC.

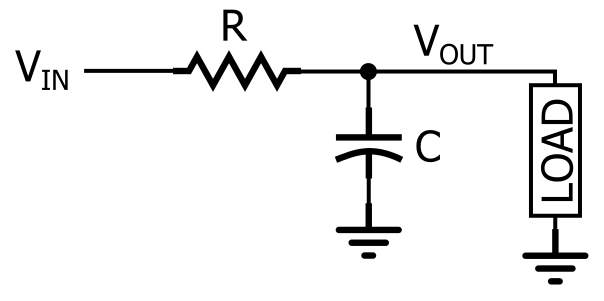
Nízkoprůchodový filtr RC.

Jak vidíte na obrázku, nízkoprůchodová odezva RC se vytvoří umístěním rezistoru do série s cestou signálu a kondenzátoru paralelně se zátěží. Na obrázku je zátěž jediná součástka, ale ve skutečném obvodu to může být něco mnohem složitějšího, například analogově-digitální převodník, zesilovač nebo vstupní stupeň osciloskopu, který používáte k měření odezvy filtru.

Intuitivně můžeme analyzovat filtrační činnost topologie RC dolní propusti, pokud si uvědomíme, že rezistor a kondenzátor tvoří dělič napětí závislý na frekvenci.

Nízkofrekvenční filtr RC překreslený tak, že vypadá jako dělič napětí.

Když je frekvence vstupního signálu nízká, je impedance kondenzátoru vysoká vzhledem k impedanci rezistoru; většina vstupního napětí tedy klesá přes kondenzátor (a přes zátěž, která je s kondenzátorem paralelní). Když je vstupní frekvence vysoká, je impedance kondenzátoru nízká v porovnání s impedancí rezistoru, což znamená, že na rezistoru klesá více napětí a méně se ho přenáší na zátěž. Nízké frekvence jsou tedy propouštěny a vysoké frekvence jsou blokovány.

Toto kvalitativní vysvětlení funkce RC dolní propusti je důležitým prvním krokem, ale není příliš užitečné, když potřebujeme obvod skutečně navrhnout, protože pojmy „vysoká frekvence“ a „nízká frekvence“ jsou velmi vágní. Inženýři potřebují vytvářet obvody, které propouštějí a blokují konkrétní frekvence. Například ve výše popsaném zvukovém systému chceme zachovat signál 5 kHz a potlačit signál 500 kHz. To znamená, že potřebujeme filtr, který přechází z propouštění na blokování někde mezi 5 kHz a 500 kHz.

Cílový kmitočet

Rozsah kmitočtů, pro které filtr nezpůsobuje výrazný útlum, se nazývá propustné pásmo a rozsah kmitočtů, pro které filtr způsobuje výrazný útlum, se nazývá pásmo zastavení. Analogové filtry, jako je například RC dolnopropustný filtr, vždy postupně přecházejí z propustného pásma do pásma zastavení. To znamená, že nelze určit jednu frekvenci, při které filtr přestane propouštět signály a začne je blokovat. Inženýři však potřebují způsob, jak pohodlně a stručně shrnout frekvenční charakteristiku filtru, a právě zde přichází ke slovu pojem mezní frekvence.

Při pohledu na graf frekvenční charakteristiky RC filtru si všimnete, že pojem „mezní frekvence“ není příliš přesný. Představa, že se spektrum signálu „rozřízne“ na dvě poloviny, z nichž jedna zůstane zachována a druhá je vyřazena, neplatí, protože útlum roste postupně s tím, jak se frekvence pohybují od frekvence pod mezní hranicí k frekvenci nad ní.

Mezní frekvence RC dolnopropustného filtru je ve skutečnosti frekvence, při níž se amplituda vstupního signálu sníží o 3 dB (tato hodnota byla zvolena proto, že snížení amplitudy o 3 dB odpovídá 50% snížení výkonu). Proto se mezní frekvence nazývá také frekvence -3 dB a ve skutečnosti je tento název přesnější a informativnější. Termín šířka pásma označuje šířku propustného pásma filtru a v případě dolnopropustného filtru je šířka pásma rovna frekvenci -3 dB (jak je znázorněno na diagramu níže).

Tento diagram vyjadřuje obecnou charakteristiku frekvenční charakteristiky dolnopropustného RC filtru. Šířka pásma je rovna frekvenci -3 dB.

Jak bylo vysvětleno výše, chování dolní propusti RC filtru je způsobeno interakcí mezi frekvenčně nezávislou impedancí rezistoru a frekvenčně závislou impedancí kondenzátoru. Abychom mohli určit podrobnosti frekvenční charakteristiky filtru, musíme matematicky analyzovat vztah mezi odporem (R) a kapacitou (C) a můžeme také manipulovat s těmito hodnotami, abychom navrhli filtr, který splňuje přesné specifikace. Mezní frekvence (fC) RC filtru s dolní propustí se vypočítá takto:

Podívejme se na jednoduchý příklad návrhu. Hodnoty kondenzátorů jsou více omezující než hodnoty rezistorů, takže začneme s běžnou hodnotou kapacity (například 10 nF) a poté pomocí rovnice určíme požadovanou hodnotu odporu. Cílem je navrhnout filtr, který zachová zvukový průběh 5 kHz a odmítne šumový průběh 500 kHz. Vyzkoušíme mezní frekvenci 100 kHz a později v článku budeme pečlivěji analyzovat vliv tohoto filtru na obě frekvenční složky.

Takto nám odpor 160 Ω v kombinaci s kondenzátorem 10 nF poskytne filtr, který se přesně blíží požadované frekvenční charakteristice.

Výpočet odezvy filtru

Teoretické chování dolnopropustného filtru můžeme vypočítat pomocí frekvenčně závislé verze typického výpočtu napěťového děliče. Výstup odporového děliče napětí je vyjádřen takto:

RC filtr používá ekvivalentní strukturu, ale místo R2 máme kondenzátor. Nejprve nahradíme R2 (v čitateli) reaktancí kondenzátoru (XC). Dále musíme vypočítat velikost celkové impedance a umístit ji do jmenovatele. Máme tedy

Reaktance kondenzátoru udává velikost odporu proti průtoku proudu, ale na rozdíl od odporu závisí velikost odporu na frekvenci signálu procházejícího kondenzátorem. Musíme tedy vypočítat reaktanci při určité frekvenci a rovnice, kterou k tomu použijeme, je následující:

V příkladu návrhu výše je R ≈ 160 Ω a C = 10 nF. Budeme předpokládat, že amplituda VIN je 1 V, takže můžeme VIN z výpočtu jednoduše odstranit. Nejprve vypočítáme amplitudu VOUT při sinusové frekvenci:

Amplituda sinusové vlny se v podstatě nemění. To je dobře, protože naším záměrem bylo zachovat sinusovku a zároveň potlačit šum. Tento výsledek není překvapivý, protože jsme zvolili mezní frekvenci (100 kHz), která je mnohem vyšší než frekvence sinusové vlny (5 kHz).

Nyní se podívejme, jak úspěšně filtr potlačí složku šumu.

Amplituda šumu je jen asi 20 % původní hodnoty.

Vizualizace odezvy filtru

Nejvhodnějším prostředkem pro vyhodnocení vlivu filtru na signál je prozkoumání grafu frekvenční charakteristiky filtru. Tyto grafy, často nazývané Bodeho grafy, mají na svislé ose velikost (v decibelech) a na vodorovné ose frekvenci; vodorovná osa má obvykle logaritmické měřítko, takže fyzická vzdálenost mezi 1 Hz a 10 Hz je stejná jako fyzická vzdálenost mezi 10 Hz a 100 Hz, mezi 100 Hz a 1 kHz atd. Toto uspořádání nám umožňuje rychle a přesně posoudit chování filtru ve velmi širokém rozsahu frekvencí.

Příklad grafu frekvenční odezvy.

Každý bod na křivce udává velikost, kterou bude mít výstupní signál, pokud má vstupní signál velikost 1 V a frekvenci rovnou příslušné hodnotě na vodorovné ose. Například při vstupní frekvenci 1 MHz bude výstupní amplituda (za předpokladu vstupní amplitudy 1 V) 0,1 V (protože -20 dB odpovídá desetinásobnému snížení).

Všeobecný tvar této křivky frekvenční odezvy vám bude velmi dobře známý, jakmile strávíte více času s filtračními obvody. Křivka je v propustném pásmu téměř dokonale plochá a pak začne rychleji klesat, jak se vstupní frekvence blíží k mezní frekvenci. Nakonec se rychlost změny útlumu, nazývaná roll-off, ustálí na 20 dB/dekádu – to znamená, že velikost výstupního signálu se sníží o 20 dB na každý desetinásobný nárůst vstupní frekvence.

Ohodnocení výkonu dolnopropustného filtru

Pokud pečlivě vykreslíme frekvenční charakteristiku filtru, který jsme navrhli dříve v článku, uvidíme, že velikostní charakteristika při 5 kHz je v podstatě 0 dB (tj, téměř nulový útlum) a velikostní charakteristika při 500 kHz je přibližně -14 dB (což odpovídá zesílení 0,2). Tyto hodnoty jsou v souladu s výsledky výpočtů, které jsme provedli v předchozí části.

Protože RC filtry mají vždy postupný přechod od propustného pásma k pásmu zastavení a protože útlum nikdy nedosáhne nekonečna, nemůžeme navrhnout „dokonalý“ filtr – tj. filtr, který nemá žádný vliv na sinusový průběh a zcela eliminuje šum. Místo toho se vždy jedná o kompromis. Pokud posuneme mezní frekvenci blíže k 5 kHz, budeme mít větší útlum šumu, ale také větší útlum sinusové vlny, kterou chceme poslat do reproduktoru. Pokud posuneme mezní frekvenci blíže k 500 kHz, budeme mít menší útlum na frekvenci sinusové vlny, ale také menší útlum na frekvenci šumu.

Fázový posun dolnopropustného filtru

Dosud jsme probírali způsob, jakým filtr mění amplitudu různých frekvenčních složek v signálu. Reaktivní obvodové prvky však vždy kromě amplitudových účinků přinášejí i fázový posun.

Pojmem fáze se rozumí hodnota periodického signálu v určitém okamžiku v rámci cyklu. Když tedy říkáme, že obvod způsobuje fázový posun, myslíme tím, že vytváří nesoulad mezi vstupním a výstupním signálem: vstupní a výstupní signál již nezačínají a nekončí své cykly ve stejném časovém okamžiku. Hodnota fázového posunu, například 45° nebo 90°, udává, jak velká nesouosost byla vytvořena.

Každý reaktivní prvek v obvodu zavádí 90° fázový posun, ale tento fázový posun nenastává najednou. Fáze výstupního signálu se stejně jako velikost výstupního signálu mění postupně s rostoucí vstupní frekvencí. V RC dolnopropustném filtru máme jeden jalový prvek (kondenzátor), a proto obvod nakonec zavede 90° fázový posun.

Stejně jako u velikostní odezvy se fázová odezva nejsnáze vyhodnocuje zkoumáním grafu, na kterém vodorovná osa označuje logaritmickou frekvenci. Níže uvedený popis vyjadřuje obecný průběh a podrobnosti pak můžete doplnit zkoumáním grafu.

Fázový posun je zpočátku 0°.
Postupně se zvyšuje, až dosáhne 45° na mezním kmitočtu; během této části odezvy se rychlost změny zvyšuje.
Po mezní frekvenci se fázový posun nadále zvyšuje, ale rychlost změny se snižuje.
Rychlost změny se stává velmi malou, když se fázový posun asymptoticky blíží 90°.

Plná čára je velikostní odezva a tečkovaná čára je fázová odezva. Mezní frekvence je 100 kHz. Všimněte si, že fázový posun je na mezním kmitočtu 45°.

Filtry dolní propusti druhého řádu

Dosud jsme předpokládali, že RC filtr dolní propusti se skládá z jednoho rezistoru a jednoho kondenzátoru. Tato konfigurace je filtrem prvního řádu.

„Řád“ pasivního filtru je určen počtem jalových prvků – tj. kondenzátorů nebo cívek – které jsou v obvodu přítomny. Filtr vyššího řádu má více jalových prvků, a to vede k většímu fázovému posunu a strmějšímu náběhu. Tato druhá charakteristika je hlavní motivací pro zvýšení řádu filtru.

Přidáním jednoho jalového prvku do filtru – např. přechodem z prvního řádu na druhý nebo z druhého na třetí řád – zvýšíme maximální roll-off o 20 dB/dekádu. Strmější roll-off znamená rychlejší přechod od nízkého útlumu k vysokému útlumu, což může vést ke zlepšení výkonu, pokud signál nemá široké frekvenční pásmo, které odděluje požadované frekvenční složky od složek šumu.

Filtry druhého řádu jsou běžně postaveny kolem rezonančního obvodu sestávajícího z induktoru a kondenzátoru (tato topologie se nazývá „RLC“ pro rezistor-induktor-kondenzátor). Je však možné vytvořit také filtry druhého řádu RC. Jak ukazuje následující schéma, stačí kaskádovat dva RC filtry prvního řádu.

Ačkoli tato topologie jistě vytváří odezvu druhého řádu, není příliš rozšířená – jak uvidíme v následující části, frekvenční odezva je často horší než u aktivního filtru druhého řádu nebo filtru RLC druhého řádu.

Frekvenční odezva RC filtru druhého řádu

O vytvoření RC dolnopropustného filtru druhého řádu se můžeme pokusit tak, že navrhneme filtr prvního řádu podle požadované mezní frekvence a poté zapojíme dva tyto stupně prvního řádu do série. Výsledkem je sice filtr s podobnou celkovou frekvenční charakteristikou a maximální odbočkou 40 dB/dekádu namísto 20 dB/dekádu.

Podíváme-li se však na charakteristiku podrobněji, zjistíme, že se frekvence -3 dB snížila. RC filtr druhého řádu se nechová podle očekávání, protože oba stupně nejsou nezávislé – nemůžeme tyto dva stupně jednoduše spojit dohromady a analyzovat obvod jako dolnopropustný filtr prvního řádu následovaný identickým dolnopropustným filtrem prvního řádu.

Navíc, i když mezi oba stupně vložíme vyrovnávací paměť, takže první RC stupeň a druhý RC stupeň mohou fungovat jako nezávislé filtry, útlum na původní mezní frekvenci bude 6 dB místo 3 dB. K tomu dochází právě proto, že oba stupně pracují nezávisle – první filtr má na mezním kmitočtu útlum 3 dB a druhý filtr přidává další 3 dB útlumu.

Základním omezením dolní propusti RC filtru druhého řádu je to, že konstruktér nemůže jemně doladit přechod z propustného do mezního pásma nastavením faktoru Q filtru; tento parametr udává, jak je tlumená frekvenční charakteristika. Pokud kaskádujete dva identické RC dolnopropustné filtry, odpovídá celková přenosová funkce odezvě druhého řádu, ale faktor Q je vždy 0,5. Pokud je Q = 0,5, je filtr na hranici přetlumení a výsledkem je frekvenční charakteristika, která se v přechodové oblasti „prohýbá“. Aktivní filtry druhého řádu a filtry založené na rezonanci druhého řádu toto omezení nemají; konstruktér může řídit faktor Q, a tím doladit frekvenční odezvu v přechodové oblasti.

Shrnutí

Všechny elektrické signály obsahují směs žádoucích a nežádoucích frekvenčních složek. Nežádoucí frekvenční složky jsou obvykle způsobeny šumem a rušením a v některých situacích negativně ovlivní výkon systému.
Filtr je obvod, který reaguje různými způsoby na různé části spektra signálu. Dolnopropustný filtr je navržen tak, aby propouštěl nízkofrekvenční složky a blokoval vysokofrekvenční složky.
Mezní frekvence dolnopropustného filtru označuje frekvenční oblast, ve které filtr přechází z nízkého útlumu na výrazný útlum.
Výstupní napětí RC dolnopropustného filtru lze vypočítat tak, že se na obvod pohlíží jako na dělič napětí, který se skládá z (frekvenčně nezávislého) odporu a (frekvenčně závislé) reaktance.
Graf závislosti velikosti (v dB, na svislé ose) na logaritmické frekvenci (v hertzích, na vodorovné ose) je vhodný a účinný způsob, jak zkoumat teoretické chování filtru. Graf závislosti fáze na logaritmické frekvenci můžete také použít k určení velikosti fázového posunu, který bude aplikován na vstupní signál.
Filtr druhého řádu poskytuje strmější odvalování; tato odezva druhého řádu je užitečná v případě, že signál neposkytuje široké pásmo oddělení mezi požadovanými frekvenčními složkami a nežádoucími frekvenčními složkami.
RC dolnopropustný filtr druhého řádu můžete vytvořit sestavením dvou identických RC dolnopropustných filtrů prvního řádu a následným připojením výstupu jednoho ke vstupu druhého. Celková frekvence -3 dB bude nižší, než se očekávalo.