Co je to trik s jádrem? Proč je důležitý?
Když se mluví o jádrech ve strojovém učení, s největší pravděpodobností vás jako první napadne model podpůrných vektorů (SVM), protože trik s jádry se v modelu SVM hojně používá k překlenutí linearity a nelinearity.
Abych vám pomohl pochopit, co je to jádro a proč je důležité, představím vám nejprve základy modelu SVM.
Model SVM je model strojového učení s dohledem, který se používá především pro klasifikaci (ale lze jej použít i pro regresi!). Učí se oddělovat různé skupiny tím, že vytváří rozhodovací hranice.

V grafu výše si všimneme, že existují dvě třídy pozorování: modré body a fialové body. Existuje spousta způsobů, jak tyto dvě třídy oddělit, jak ukazuje graf vlevo. My však chceme najít „nejlepší“ hyperplochu, která by maximalizovala rozpětí mezi těmito dvěma třídami, což znamená, že vzdálenost mezi hyperplochou a nejbližšími datovými body na každé straně je největší. Podle toho, na které straně hyperplochy se nový datový bod nachází, bychom mohli novému pozorování přiřadit třídu.
Ve výše uvedeném příkladu to zní jednoduše. Ne všechna data jsou však lineárně separovatelná. Ve skutečnosti jsou v reálném světě téměř všechna data náhodně rozložená, což ztěžuje lineární separaci různých tříd.

Proč je důležité používat trik s jádrem?
Jak vidíte na výše uvedeném obrázku, pokud najdeme způsob, jak zmapovat data z dvourozměrného prostoru do trojrozměrného prostoru, budeme schopni najít rozhodovací plochu, která jasně rozděluje mezi různé třídy. Moje první myšlenka tohoto procesu transformace dat je namapovat všechny datové body do vyšší dimenze (v tomto případě 3 dimenze), najít hranici a provést klasifikaci.
To zní v pořádku. Když je však rozměrů stále více, výpočty v tomto prostoru jsou stále dražší. Tehdy přichází na řadu trik s jádrem. Umožňuje nám pracovat v původním prostoru příznaků, aniž bychom museli počítat souřadnice dat ve vyšším dimenzionálním prostoru.
Podívejme se na příklad:
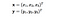
Tady x a y jsou dva datové body ve 3 rozměrech. Předpokládejme, že potřebujeme mapovat x a y do 9rozměrného prostoru. Musíme provést následující výpočty, abychom získali konečný výsledek, kterým je právě skalár. Výpočetní složitost je v tomto případě O(n²).

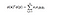
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
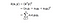
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Jakékoli výpočty zahrnující bodové součin (x, y) mohou využít trik jádra.
Různé funkce jádra
Existují různá jádra. Mezi nejoblíbenější patří polynomiální jádro a jádro s radiální bázovou funkcí (RBF).
„Intuitivně se polynomiální jádro dívá nejen na dané vlastnosti vstupních vzorků, aby určilo jejich podobnost, ale také na jejich kombinace“ (Wikipedie), stejně jako výše uvedený příklad. S n původními rysy a d stupni polynomu dává polynomické jádro n^d rozšířených rysů.
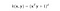
.
Jádro RBF se také nazývá Gaussovo jádro. V prostoru příznaků existuje nekonečný počet dimenzí, protože jej lze rozšířit Taylorovou řadou. V níže uvedeném formátu Parametr γ určuje, jak velký vliv má jeden trénovací příklad. Čím je větší, tím blíže musí být ostatní příklady, aby byly ovlivněny (dokumentace sklearn).
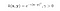
V knihovně sklearn v jazyce Python existují různé možnosti funkcí jádra. V případě potřeby si můžete vytvořit i vlastní jádro.
Konec
Tento trik s jádrem zní jako „dokonalý“ plán. Je však třeba mít na paměti jednu zásadní věc: když mapujeme data na vyšší dimenzi, existuje pravděpodobnost, že model přenastavíme. Velmi důležitá je tedy volba správné funkce jádra (včetně správných parametrů) a regularizace.
Pokud vás zajímá, co je to regularizace, napsal jsem článek pojednávající o tom, jak ji chápu já, a najdete ho zde.
Doufám, že se vám tento článek bude líbit. Jako vždy mi prosím dejte vědět, pokud máte nějaké dotazy, připomínky, návrhy atd. Děkuji za přečtení 🙂