dB: Co je to decibel?

Zvukový tlak, hladina zvuku a dB. Zvuk se obvykle měří pomocí mikrofonů a ty reagují úměrně akustickému tlaku, p. Nyní platí, že výkon ve zvukové vlně, při zachování všech ostatních podmínek, roste jako čtverec tlaku. (Podobně elektrický výkon v rezistoru roste jako kvadrát napětí.) Logaritmus x2 je prostě 2 logaritmy x, takže při přepočtu tlakových poměrů na decibely se zavádí faktor 2. Rozdíl hladin akustického tlaku mezi dvěma zvuky o hodnotách p1 a p2 je tedy:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (v celém textu se logaritmuje na základ 10).

Co se stane, když snížíte výkon zvuku na polovinu? Logaritmus 2 je 0,3010, takže logaritmus 1/2 je -0,3, s dobrým přiblížením. Pokud tedy snížíte výkon na polovinu, snížíte výkon a hladinu zvuku o 3 dB. Pokud jej opět snížíte na polovinu (na 1/4 původního výkonu), snížíte hladinu o další 3 dB. Pokud budete pokračovat ve snižování výkonu na polovinu, získáte tyto poměry.

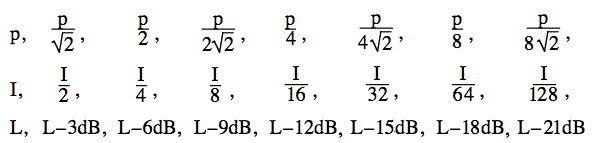
Co se stane, když přidám dva stejné zvuky? Zdvojnásobím intenzitu (zvýšení o 3 dB)? Nebo zdvojnásobím tlak (zvýšení o 6 dB)? Tato často kladená otázka je poněkud záludná, a proto se jí věnujeme zde v našich často kladených dotazech.

Zvukové soubory pro zobrazení velikosti decibelu

Výše jsme viděli, že snížení výkonu na polovinu sníží akustický tlak o √2 a hladinu zvuku o 3 dB. To jsme provedli v prvním grafickém a zvukovém souboru níže.

První ukázka zvuku je bílý šum (směs širokého spektra slyšitelných frekvencí, analogicky bílému světlu, které je směsí všech viditelných frekvencí). Druhý vzorek je stejný šum, jehož napětí je sníženo o faktor √2. Nyní je 1/√2 přibližně 0,7, takže -3 dB odpovídá snížení napětí nebo tlaku na 70 % původní hodnoty. Zelená čára ukazuje napětí jako funkci času. Červená čára ukazuje spojitý exponenciální pokles s časem. Všimněte si, že napětí klesá o 50 % pro každý druhý vzorek. Všimněte si také, že zdvojnásobení výkonu nemá na hlasitost velký vliv. Probereme to dále, ale je to užitečná věc, kterou je třeba mít na paměti při výběru zařízení pro reprodukci zvuku. Zvukové soubory a animace vytvořili John Tann a George Hatsidimitris.

Jak velký je decibel? V další sérii jsou po sobě jdoucí vzorky zmenšeny právě o jeden decibel.

Jeden decibel má stejný řád jako právě zaznamenatelný rozdíl (Just Noticeable Difference, JND) pro hladinu zvuku. Při poslechu těchto souborů si všimnete, že poslední je tišší než první, ale pro ucho je poněkud méně zřejmé, že druhý z každé dvojice je tišší než jeho předchůdce. 10*log10(1,26) = 1, takže pro zvýšení hladiny zvuku o 1 dB je třeba zvýšit výkon o 26 % nebo napětí o 12 %.

Co když je rozdíl menší než jeden decibel? Hladiny zvuku se zřídkakdy udávají s desetinnými místy. Důvodem je, že hladiny zvuku, které se liší o méně než 1 dB, jsou těžko rozlišitelné, jak ukazuje další příklad (díky tomu je dB vhodnou jednotkou velikosti)

0,3 dB kroků. Můžete si všimnout, že poslední dvojice je tišší než první, ale rozdíl mezi po sobě jdoucími dvojicemi je obtížné zaznamenat. 10*log10(1,07) = 0,3, takže pro zvýšení hladiny zvuku o 0,3 dB je třeba zvýšit výkon o 7 % nebo napětí o 3,5 %.

Standardní referenční úrovně. („absolutní“ hladina zvuku)

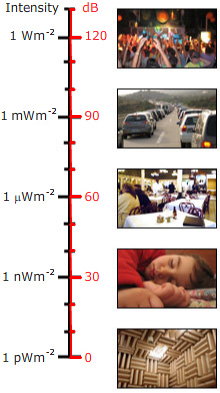Výše jsme uvedli, že decibel je poměr. Pokud se tedy používá k udání hladiny zvuku pro jeden zvuk, a nikoli jako poměr, je třeba zvolit referenční hladinu. Pro hladinu akustického tlaku se obvykle volí referenční hladina (pro vzduch) pref = 20 mikropascalů (20 μPa) nebo 0,02 mPa. To je velmi nízká hodnota: jedná se o 2 desetimiliardtiny atmosféry. Nicméně je to přibližně hranice citlivosti lidského ucha v jeho citlivém frekvenčním rozsahu. (Obvykle se tato citlivost vyskytuje pouze u poměrně mladých lidí nebo u lidí, kteří nebyli vystaveni hlasité hudbě nebo jiným hlasitým zvukům. Osobní hudební systémy s reproduktory do uší jsou schopny dosáhnout velmi vysokých hladin zvuku v uchu a podle některých názorů jsou zodpovědné za velkou část ztráty sluchu u mladých dospělých v některých zemích).

Pokud tedy čtete o hladině akustického tlaku 86 dB, znamená to, že

20 log (p2/pref) = 86 dB

kde pref je akustický tlak referenční hladiny a p2 hladiny daného zvuku. Obě strany vydělte 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 je logaritmus 10 tisíc, 0,3 je logaritmus 2, takže tento zvuk má akustický tlak 20tisíckrát větší než referenční hladina (p2/pref = 20 000) neboli intenzitu 400milionkrát větší než intenzita referenční. 86 dB je silný zvuk, ale není nebezpečný – za předpokladu, že expozice je krátká.

Co znamená 0 dB? Tato hladina nastává, když se naměřená intenzita rovná referenční hladině, tj. je to hladina zvuku odpovídající 0,02 mPa. V tomto případě máme

hladina zvuku = 20 log (pměřená/pref) = 20 log 1 = 0 dB

Nezapomeňte, že decibely měří poměr. Hodnota 0 dB nastane, když vezmeme logaritmus poměru 1 (log 1 = 0). 0 dB tedy neznamená žádný zvuk, ale hladinu zvuku, při které se akustický tlak rovná referenční hladině. Jedná se o malý tlak, ale ne nulový. Je také možné mít záporné hladiny zvuku: – 20 dB by znamenalo zvuk s tlakem 10krát menším než referenční tlak, tj. 2 μPa.

Ne všechny zvukové tlaky jsou stejně hlasité. Je to proto, že lidské ucho nereaguje na všechny frekvence stejně: jsme mnohem citlivější na zvuky ve frekvenčním rozsahu přibližně 1 kHz až 7 kHz (1000 až 7000 kmitů za sekundu) než na zvuky s velmi nízkou nebo vysokou frekvencí. Z tohoto důvodu jsou zvukoměry obvykle vybaveny filtrem, jehož odezva na frekvenci je trochu podobná odezvě lidského ucha. (Více o těchto filtrech níže.) Pokud je použit „váhový filtr A“, udává se hladina akustického tlaku v jednotkách dB(A) nebo dBA. Hladinu akustického tlaku na stupnici dBA lze snadno měřit, a proto se hojně používá. Jedním z důvodů, proč se liší od hlasitosti, je skutečnost, že filtr nereaguje stejným způsobem jako ucho. Abychom pochopili hlasitost zvuku, je třeba nejprve konzultovat některé křivky znázorňující frekvenční odezvu lidského ucha, které jsou uvedeny níže. (Případně si můžete změřit vlastní sluchovou odezvu.) Dalším důvodem je, že lidský sluch není logaritmický.

Logaritmické míry

Proč používáme decibely? Ucho je schopno slyšet velmi široký rozsah zvuků: poměr akustického tlaku, který způsobuje trvalé poškození při krátkodobém působení, k hranici, kterou (nepoškozené) ucho slyší, je více než milion. Pro práci s takovým rozsahem jsou užitečné logaritmické jednotky: logaritmus milionu je 6, takže tento poměr představuje rozdíl 120 dB. Sluch ze své podstaty nemá logaritmickou odezvu. (Logaritmické míry jsou užitečné také tehdy, když se zvuk (krátce) exponenciálně zvyšuje nebo snižuje v čase. K tomu dochází v mnoha aplikacích zahrnujících proporcionální zesílení nebo proporcionální ztrátu.“

Filtry používané pro dBA a dB(C)

Nejpoužívanějším filtrem hladiny zvuku je stupnice A, která zhruba odpovídá inverzní křivce rovnoměrné hlasitosti 40 dB (při 1 kHz). Při použití tohoto filtru je tedy zvukoměr méně citlivý na velmi vysoké a velmi nízké frekvence. Měření provedená na této stupnici se vyjadřují v dBA. Stupnice C se v průběhu několika oktáv mění jen málo, a proto je vhodná pro subjektivní měření pouze pro střední až vysoké hladiny zvuku. Měření na této stupnici se vyjadřují jako dB(C). Existuje také (zřídka používaná) váhová stupnice B, která je prostřední mezi stupnicemi A a C. Na obrázku níže je znázorněna odezva filtru A (vlevo) a filtru C, přičemž zisky v dB jsou uvedeny vzhledem k 1 kHz. (Úvod do problematiky filtrů naleznete v části RC filtry, integrátory a diferenciátory).



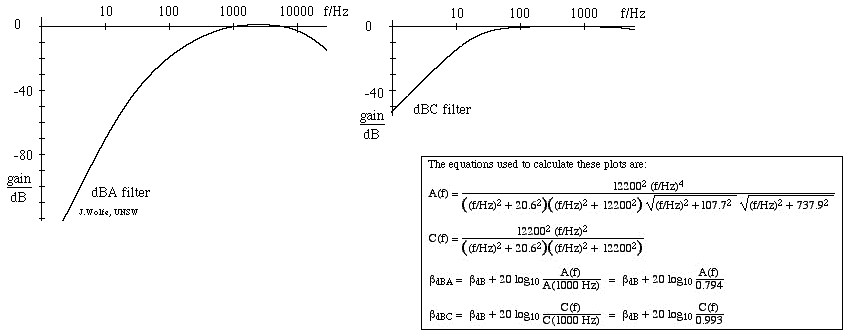
Na stránkách hudební akustiky a akustiky řeči vykreslujeme zvuková spektra v dB. Důvodem této běžné praxe je velký rozsah měřených akustických tlaků.

Při měření dB(G) se používá úzkopásmový filtr, který dává vysokou váhu frekvencím mezi 1 a 20 Hz a nízkou váhu ostatním. Poskytuje tedy velké hodnoty pro zvuky a infrazvuky, které nejsou snadno slyšitelné. ISO 7196:1995

Hlučnost, fon a son, křivky sluchové odezvy

Fon je jednotka, která je vztažena k dB podle psychofyzikálně změřené frekvenční charakteristiky ucha. Při frekvenci 1 kHz jsou údaje ve fononech a dB z definice stejné. Pro všechny ostatní frekvence je stupnice phon určena na základě výsledků experimentů, při nichž byli dobrovolníci požádáni, aby upravili hlasitost signálu na dané frekvenci, dokud neposoudili jeho hlasitost jako rovnou hlasitosti signálu o frekvenci 1 kHz. K převodu z dB na fonony potřebujete graf takových výsledků. Takový graf závisí na hladině zvuku: při vysokých hladinách zvuku je plošší.

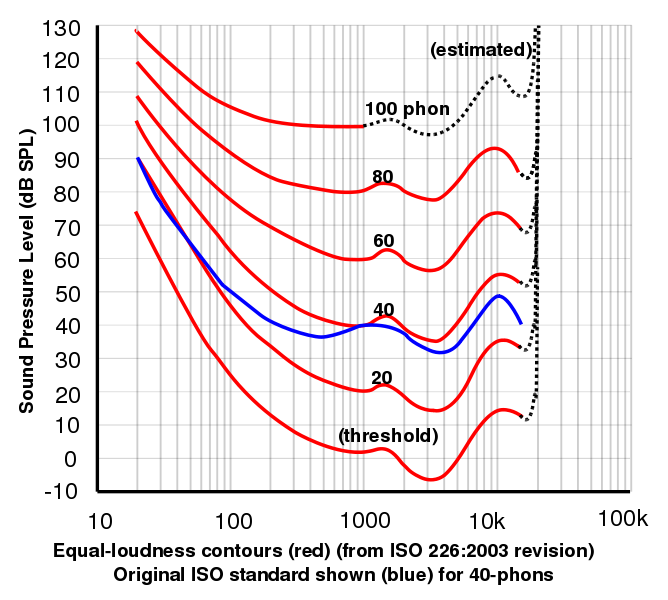
Tento graf s laskavým svolením společnosti Lindosland ukazuje údaje Mezinárodní organizace pro normalizaci z roku 2003 pro křivky stejné hlasitosti stanovené experimentálně. Grafy stejné hlasitosti jako funkce frekvence se často obecně nazývají Fletcher-Munsonovy křivky podle původní práce Fletcher, H. a Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Vlastní křivky si můžete vytvořit pomocí našich stránek o odezvě sluchu.

Sonda je odvozena z psychofyzikálních měření, při kterých dobrovolníci upravovali zvuky tak dlouho, dokud je neposoudili jako dvakrát hlasitější. To umožňuje vztáhnout vnímanou hlasitost k fonům. Jeden son je definován jako 40 fonů. Experimentálně bylo zjištěno, že nad 40 fonů odpovídá zvýšení hladiny zvuku o 10 dB přibližně zdvojnásobení vnímané hlasitosti. Tato aproximace se tedy používá při definici sonu: 1 son = 40 fonů, 2 sony = 50 fonů, 4 sony = 60 fonů atd.



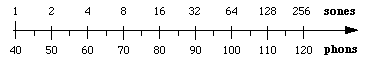
Z tohoto vztahu vyplývá, že hlasitost a intenzita souvisí podle mocninného zákona: hlasitost v sonech je úměrná (intenzita)log 2 = (intenzita)0,3.

Nebylo by skvělé umět převádět z dB (které lze měřit přístrojem) na tóny (které přibližují hlasitost vnímanou lidmi)? To se někdy dělá pomocí tabulek, které najdete v akustických příručkách. Pokud vám však nevadí poněkud hrubá aproximace, můžete říci, že váhová křivka A aproximuje lidskou frekvenční odezvu při nízkých až středních hladinách zvuku, takže dB(A) je velmi zhruba stejná jako fonony, a to v omezeném rozsahu nízkých hladin. Pak lze použít výše popsaný logaritmický vztah mezi zvuky a fonony.

Hladina záznamu a decibely

Měřiče měřící úroveň záznamu nebo výstupní úroveň na zvukových elektronických zařízeních (mixážní pulty atd.) téměř vždy zaznamenávají efektivní hodnotu střídavého napětí (viz odkazy, kde se dozvíte o střídavém a efektivním napětí). Pro daný odpor R je výkon P roven V2/R, takže
rozdíl v úrovni napětí = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, nebo

absolutní úroveň napětí = 20 log (V/Vref)

kde Vref je referenční napětí. Jaké je tedy referenční napětí?

Zřejmá úroveň, kterou je třeba zvolit, je jeden efektivní volt a v tomto případě se úroveň zapisuje jako dBV. To je racionální a také výhodné u analogově-digitálních karet, jejichž maximální rozsah je často přibližně jeden volt rms. Je tedy třeba pamatovat na to, aby úroveň byla v záporných dBV (méně než jeden volt), aby nedocházelo k ořezávání špiček signálu, ale ne příliš záporných (aby váš signál byl stále mnohem větší než šum pozadí).

Někdy uvidíte dBm. Dříve to znamenalo decibely elektrického výkonu vzhledem k jednomu miliwattu a někdy to tak stále je. Z historických důvodů je to však složitější. V polovině dvacátého století mělo mnoho zvukových linek jmenovitou impedanci 600 Ω. Pokud je impedance čistě odporová a pokud nastavíte V2/600 Ω = 1 mW, pak dostanete V = 0,775 voltu. Pokud jste tedy používali zátěž 600 Ω, 1 mW výkonu byl 0 dBm, což bylo 0,775 V, takže jste takto kalibrovali své měřiče úrovně. Problém vznikl proto, že jakmile je hladinoměr, který měří napětí, takto zkalibrován, bude ukazovat 0 dBm při 0,775 V, i když není připojen k 600 Ω. Takže, možná nelogicky, dBm bude někdy znamenat dB vzhledem k 0,775 V. (Když jsem byl kluk, byly kalkulačky drahé, takže jsem používal tátovo staré posuvné pravidlo, které mělo na okénku kurzoru vyznačen faktor 0,775, aby se takové výpočty usnadnily).

Jak převést dBV nebo dBm na dB hladiny zvuku? Neexistuje žádný jednoduchý způsob. Záleží na způsobu převodu elektrického výkonu na zvukový výkon. I když je elektrický signál připojen přímo k reproduktoru, bude převod záviset na účinnosti a impedanci reproduktoru. A samozřejmě může existovat výkonový zesilovač a různé akustické komplikace mezi místem, kde měříte dBV na mixážním pultu, a místem, kde jsou vaše uši ve zvukovém poli.

Intenzita, vyzařování a dB

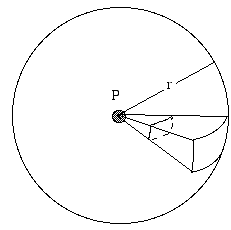
Jak závisí hladina zvuku (nebo úroveň rádiového signálu atd.) na vzdálenosti od zdroje?

Zdroj, který vyzařuje záření stejně do všech směrů, se nazývá izotropní. Uvažujme izolovaný zdroj zvuku, vzdálený od jakýchkoli odrazných ploch – třeba ptáka zpívajícího vysoko ve vzduchu. Představte si kouli o poloměru r, jejímž středem je zdroj. Zdroj vyzařuje spojitě celkový výkon P. Tento zvukový výkon se šíří a prochází povrchem koule. Je-li zdroj izotropní, je intenzita I na tomto povrchu z definice všude stejná. Intenzita I je definována jako výkon na jednotku plochy. Plocha povrchu koule je 4πr2, takže výkon (v našem příkladu zvukový výkon) procházející každým čtverečním metrem povrchu je podle definice:

I = P/4πr2.

Vidíme tedy, že pro izotropní zdroj je intenzita nepřímo úměrná čtverci vzdálenosti od zdroje:

I2/I1 = r12/r22.

Ale intenzita je úměrná kvadrátu akustického tlaku, takže bychom mohli stejně tak napsat:

p2/p1 = r1/r2.

Zdvojnásobíme-li tedy vzdálenost, snížíme akustický tlak o faktor 2 a intenzitu o faktor 4: jinými slovy snížíme hladinu zvuku o 6 dB. Zvýšíme-li r o faktor 10, snížíme hladinu o 20 dB atd.

Upozorňujeme však, že mnoho zdrojů není izotropních, zejména pokud je vlnová délka menší nebo velikostně srovnatelná se zdrojem. Dále jsou často poměrně důležité odrazy, zejména pokud je v blízkosti země nebo pokud se nacházíte v interiéru.

Tlak, intenzita a měrná impedance

Pro akustické vlny je měrná akustická impedance z definována jako poměr akustického tlaku p a průměrné rychlosti částic u, způsobené zvukem ave, z = p/u . V článku Akustická impedance, intenzita a výkon si ukážeme, jak souvisí efektivní akustický tlak p a intenzita I:
I = p2/z

Pro vzduch je měrná akustická impedance z 420 kg.s-1.m-2 = 420 Pa.s.m-1 . Pro (sladkou) vodu je specifická akustická impedance pro vodu 1,48 MPa.s.m-1. Zvuková vlna ve vodě o stejném tlaku má tedy mnohem menší intenzitu než vlna ve vzduchu.

dBi a záření, které se mění podle směru

Záření, které se mění podle směru, se nazývá anizotropní. Pro mnoho případů v komunikaci je izotropní záření neekonomické: proč vysílat podstatnou část výkonu směrem nahoru, pokud je přijímač, stejně jako vy, relativně blízko u země. Pro zvuk krátkých vlnových délek (včetně většiny rozsahu důležitého pro řeč) může megafon pomoci, aby váš hlas byl více anizotropní. U rádia umožňuje široká škála konstrukcí antén vysokou anizotropii pro vysílání i příjem.

Zajímá-li vás tedy vyzařování v určitém směru (nebo příjem z něj), chcete, aby poměr intenzity naměřené v tomto směru v dané vzdálenosti byl vyšší než poměr intenzity naměřené ve stejné vzdálenosti od izotropního zářiče (nebo přijímané izotropním přijímačem). Tento poměr se nazývá zisk; vyjádřete jej v dB a získáte zisk v dBi pro daný zářič. Tato jednotka se používá hlavně pro antény, ať už vysílací nebo přijímací, ale někdy se používá i pro zdroje zvuku a směrové mikrofony.

Příkladové úlohy

Několik lidí napsalo žádost o příklady použití dB ve výpočtech. Takže…
• Za stejných podmínek, o kolik je hlasitější reproduktor poháněný (ve svém lineárním rozsahu) zesilovačem o výkonu 100 W než zesilovačem o výkonu 10 W?

  Výkony se liší desetinásobně, což je, jak jsme viděli výše, 10 dB. Vše ostatní stejné zde znamená, že frekvenční odezvy jsou stejné a že je použit stejný vstupní signál atd. Frekvenční závislost by tedy měla být stejná. Deset dB odpovídá deseti fonům. Abyste dosáhli vnímaného zdvojnásobení hlasitosti, potřebujete nárůst o 10 fonů. Reproduktor poháněný zesilovačem o výkonu 100 W je tedy dvakrát hlasitější, než když je poháněn zesilovačem o výkonu 10 W, za předpokladu, že zůstanete v lineárním rozsahu a nezkreslíte nebo nezničíte reproduktor. (Zesilovač o výkonu 100 W produkuje dvakrát více fonů než zesilovač o výkonu 10 W.)

• Stojím ve vzdálenosti R od malého zdroje zvuku (velikost mnohem menší než R), na úrovni země na volném prostranství, kde lze zanedbat odrazy. Hladina zvuku je L. Pokud se nyní přesunu do vzdálenosti nR (n je číslo a nR je stále mnohem větší než velikost zdroje), jaká bude nová hladina zvuku?

  Nejprve si uvědomte, že zanedbání odrazů je velmi důležité. Tento výpočet nebude fungovat uvnitř místnosti, kde odrazy od stěn (společně vytvářející dozvuk) výpočet značně ztěžují. Venku je intenzita zvuku úměrná 1/r2, kde r je vzdálenost od zdroje. (Konstanta úměrnosti závisí na tom, jak dobře se odráží od země, a nás se zde netýká, protože se při výpočtu zhruba vyruší, pokud je r přiměřeně velké). Pokud tedy zvětšíme r z R na nR, snížíme intenzitu z I na I/n 2.

  Rozdíl v decibelech mezi dvěma signály o intenzitě I 2 a I 1 je definován výše takto

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Příklad pokud je n 2 (tj. pokud jdeme dvakrát dále), intenzita se sníží čtyřnásobně a hladina zvuku klesne z L na (L – 6 dB).

• Pokud v ideálních tichých podmínkách slyší mladý člověk tón o frekvenci 1 kHz a hlasitosti 0 dB, který je vysílán reproduktorem (možná měkkým reproduktorem?), o kolik se musí zvýšit výkon reproduktoru, aby se zvuk zvýšil na 110 dB (nebezpečně hlasitá, ale přežitelná úroveň)?

  Rozdíl v decibelech mezi dvěma signály o výkonu P2 a P1 je výše definován takto

  ΔL = 10 log (P2/P1) dB, takže zvýšením o 10 na výkon těchto dvou stejných veličin:
  10L/10 = P2/P1 takže:
  P2/P1 = 10110/10 = 1011 = sto tisíc milionů.

  což je ukázka toho, že lidské ucho má pozoruhodně velký dynamický rozsah, možná větší než oko.

• Zesilovač má na vstupu napětí 10 mV a na výstupu napětí 2 V. Jaké je jeho napěťové zesílení v dB?

  Napětí, stejně jako tlak, se ve výrazech pro výkon nebo intenzitu objevuje ve čtverci. (Výkon rozptýlený v rezistoru R je V2/R.) Podle konvence tedy definujeme:

  zisk = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (Ve výše uvedených akustických případech jsme viděli, že poměr tlaku vyjádřený v dB je stejný jako poměr výkonu: to byl důvod pro faktor 20 při definici dB pro tlak. Stojí za povšimnutí, že v příkladu s napěťovým zesílením se výkonové zesílení zesilovače pravděpodobně nebude rovnat napěťovému zesílení, které je definováno zde použitou konvencí. Výkon je úměrný kvadrátu napětí v daném rezistoru. Vstupní a výstupní impedance zesilovačů se však často značně liší. Například nárazníkový zesilovač nebo emitorový sledovač má napěťové zesílení přibližně 1, ale velké proudové zesílení).

• Jaký je rozdíl v dB mezi intenzitou ozáření (intenzitou světla) na Zemi (8,3 světelných minut od Slunce) a na Uranu (160 světelných minut)?

  Stejně jako u zvuku klesá izotropní intenzita světla jako r-2, takže poměr intenzity je (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Bezpečnost a ochrana zdraví při práci

Různé země a provincie mají samozřejmě různé zákony týkající se expozice hluku při práci, které jsou prosazovány s různým nadšením. Mnoho takových předpisů stanoví limit pro expozici trvalému hluku 85 dB(A) pro osmihodinovou směnu. Za každé zvýšení o 3 dB se povolená expozice snižuje na polovinu. Pokud tedy pracujete v nočním klubu, kde zesílená hudba produkuje v blízkosti vašich uší 100 dB(A), je povolená expozice 15 minut. Existuje limit pro impulsní hluk, jako jsou střelné zbraně nebo nástroje, které používají výbušné střely. (Např. špičková hodnota 140 dB by neměla být překročena kdykoli během dne.) Existuje mnoho dokumentů, které poskytují rady, jak snížit expozici hluku u zdroje (tj. snížit úroveň hudby), mezi zdrojem a uchem (tj. vzdálit se od reproduktorů na koncertě) a u ucha (tj. nosit špunty do uší nebo průmyslové chrániče sluchu). Řízení hluku a ochrana sluchu při práci je kodex praxe ve státě Nový Jižní Wales v Austrálii (adresa autora).

Několik často kladených otázek

• Jak hlasité je letadlo? Vlak? Zpívající člověk? Štěkot psa? Elektrické nářadí? Odpovědi na tuto otázku se značně liší. Velmi záleží na tom, jak daleko jste, zda jste uvnitř nebo ne, zda existuje dozvuk, jak silný je konkrétní zdroj a jaké je jeho spektrum. Uvádět hodnoty, aniž by byly podmínky zcela konkrétní, by bylo poněkud zavádějící. Protože zbytek této stránky má být spolehlivý, pokud to jde, raději bych zde hodnoty neuváděl.
• Jak se „sčítají decibely“, tedy jakou hladinu zvuku dostanete, když k hladině b přičtete hladinu a? Pokud jsou zdroje koherentní (což obvykle znamená, že nakonec pocházejí ze stejného zdroje), pak může dojít ke komplikovaným interferenčním efektům. Ve většině případů, kdy jsou zdroje nezávislé, lze intenzity sečíst a poté převést na decibely. Pokud jsou však dány hladiny zvuku v dB(A), není tak snadné se vrátit k intenzitě a je třeba vědět něco o spektru zvuku. Pokud znáte rozložení zvuku v různých frekvenčních pásmech, můžete použít applet na tomto odkazu.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.