Marginální rozdělení

Rozdělení pravděpodobnosti > Marginální rozdělení

Co je to marginální rozdělení?

Podívejte se na video nebo si přečtěte článek níže:

Technická definice může při pohledu na ni trochu zamotat hlavu:

Definice marginálního rozdělení = Jsou-li X a Y diskrétní náhodné veličiny a f (x,y) je hodnota
jejich společného rozdělení pravděpodobnosti v bodě (x,y), jsou funkce dány:
g(x) = Σy f (x,y a h(y = Σx f (x,y) jsou mezní rozdělení X a Y , resp.

Pokud vám jdou rovnice dobře od ruky, je to asi vše, co potřebujete vědět. Říká vám to, jak najít marginální rozdělení. Pokud vás však z tohoto vzorce bolí hlava (což většinu lidí bolí!), můžete k nalezení marginálního rozdělení použít tabulku rozdělení četností.

Marginální rozdělení dostalo svůj název proto, že se objevuje na okraji tabulky rozdělení pravděpodobnosti.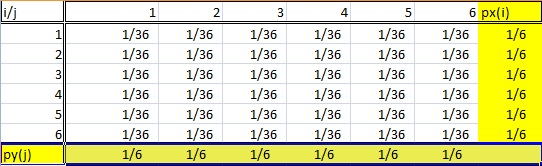

Ještěže to není tak jednoduché. Nemůžete se prostě podívat na jakoukoli starou tabulku rozdělení četností a říct, že poslední sloupec (nebo řádek) je „marginální rozdělení“. Okrajová rozdělení se řídí několika pravidly:

• Rozdělení musí pocházet z dvourozměrných dat. Dvourozměrné je jen jiný způsob, jak říci „dvě proměnné“, například X a Y. Ve výše uvedené tabulce pocházejí náhodné veličiny i a j z hodu dvěma kostkami.
• Marginální rozdělení je takové, kdy vás zajímá pouze jedna z náhodných veličin . Jinými slovy, buď X, nebo Y. Pokud se podíváte na výše uvedenou tabulku pravděpodobnosti, jsou součtové pravděpodobnosti jedné proměnné uvedeny ve spodním řádku a ostatní součtové pravděpodobnosti jsou uvedeny v pravém sloupci. Tato tabulka má tedy dvě marginální rozdělení.

Rozdíl mezi marginálním a podmíněným rozdělením.

Podmíněné rozdělení je takové, kdy nás zajímá pouze určitá subpopulace celého našeho souboru dat. V příkladu s hodem kostkou to může být „hod dvojkou“ nebo „hod šestkou“. Následující obrázek ukazuje dvě zvýrazněné dílčí populace (a tedy dvě podmíněná rozdělení).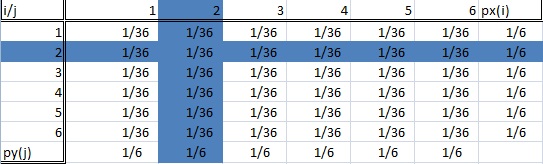

Jak vypočítat marginální rozdělení pravděpodobnosti

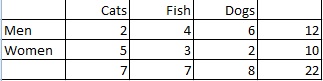
Příkladová otázka: Vypočítejte mezní rozdělení preferencí domácích zvířat mezi muži a ženami:
Řešení:
Krok 1: Spočítejte celkový počet osob. V tomto případě je celkový počet uveden v pravém sloupci (22 lidí).
Krok 2: Spočítejte počet lidí, kteří dávají přednost jednotlivým typům domácích mazlíčků, a poté tento poměr převeďte na pravděpodobnost:
Lidé, kteří dávají přednost kočkám: 7/22 = ,32
Lidé, kteří dávají přednost rybám: 7/22 = ,32
Lidé, kteří dávají přednost psům: 8/22 = ,36
Tip: Svou odpověď můžete zkontrolovat tak, že se ujistíte, že všechny pravděpodobnosti jsou rovny 1.

Příkladová otázka 2 (vzájemně se vylučující události): Pokud je P(A) = 0,20, P(b) = 0,70 a obě události se vzájemně vylučují, najděte P(B’∩A), P(B’∩A‘) a P(B∩A‘).
Pokud tento zápis neznáte, P(A‘) znamená „ne A“ neboli doplněk. P(B’∩A) znamená „průnik ne B a A“).

Odpověď:
Mohli byste si pravděpodobnosti vypočítat jednotlivě, ale mnohem jednodušší je zjistit je pomocí tabulky.

Krok 1: Vyplňte tabulku četností s danými informacemi. Celková pravděpodobnost se musí rovnat 1, takže ji můžete přičíst i k okrajům(součtům). Jednoduché sčítání/algebra doplní okrajová prázdná místa. Například ve spodním řádku 0,70 + x = 1,00, takže marginální součet pro B‘ musí být 0,30.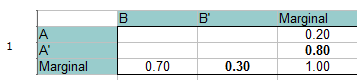

Krok 2: Přičtěte 0 pro průsečík A a B, v levé horní části tabulky. Můžeš to udělat, protože A a B se navzájem vylučují a nemohou se vyskytovat společně.

Krok 3: Doplň zbytek prázdných políček pomocí jednoduchého sčítání/algebry.

Přečtěte si z tabulky (podívejte se na průsečíky obou uvedených pravděpodobností):
P(B’∩A) = 0,20
P(B’∩A‘) = 0,10
P(B∩A‘) = 0,70.

Příkladová otázka 3 (nezávislé události): Pokud je P(A) = 0,20, P(b) = 0,70 a obě události jsou nezávislé, najděte P(B’∩A), P(B’∩A‘) a P(B∩A‘).

Odpověď: Tentokrát jsou A a B nezávislé, takže pravděpodobnost, že nastanou obě současně, je 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Tato hodnota jde do levého horního rohu (průsečík A a B). Zbytek tabulky vyplňte úplně stejně jako v předchozích krocích.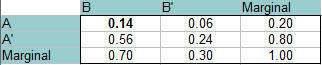

Odpovědi z tabulky (z průsečíků obou pravděpodobností):
P(B’∩A): 0.06
P(B’∩A‘): 0,24
P(B∩A‘): 0,56.

Beyer, W. H. CRC Standard Mathematical Tables, 31. vyd. Boca Raton, FL: CRC Press, str. 536 a 571, 2002.
Agresti A. (1990): Analýza kategoriálních dat. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines). 2. vydání. McGraw-Hill Education

——————————————————————————

Potřebujete pomoci s domácím úkolem nebo testovou otázkou? Se službou Chegg Study můžete získat řešení svých otázek krok za krokem od odborníka v oboru. Prvních 30 minut s lektorem Chegg je zdarma!