Solving the Königsberg Bridge Problem

This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)

The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem

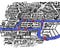
Have a look at the map above.

It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.

A map of the city is below. Můžete se podívat na oba diagramy – oba zachycují klíčové informace: které fleky země jsou spojeny s kterými dalšími fleky země a kolika mosty.

V technické řeči to znázorňujeme jako graf. Kapky země jsou vrcholy a mosty jsou hrany. Ale to není důležité.

Problém spočívá v tom, zda je možné najít trasu, která vede přes každý most přesně jednou. To znamená, že při procházce městem chceme, aby naše trasa přešla přes každý most, ale nemůže přes něj přejít dvakrát nebo třikrát… V podstatě pokud se ocitnete na stejném mostě jako předtím, je cesta neplatná. Pokud dokončíte procházku a na mostě, přes který jste nešli, je vaše trasa neplatná.

Řešení

Přemýšlejte o každém kousku země. Každý most je spojen se dvěma bloby země (tak fungují mosty). Ke každému blobu země je shodou okolností připojen lichý počet mostů.

Nyní se zamysleme nad tím, jak by vypadala platná procházka.

Když se vydáte na procházku, zaznamenáte si do poznámkového bloku každý okamžik, kdy se nacházíte v určitém blobu země. Pokud například začnete v nejjižnějším cípu města, zaznamenáte si to (vyfotíte, koupíte suvenýr…), a pokud se tam ocitnete znovu, zvýšíte počet bodů pro jižní sektor na dva.

Pro každou kapku země existují dva případy

(1) jedná se o úsek města, ve kterém ani nezačínáme procházku, ani v něm nekončíme

(2) jedná se o úsek města, ve kterém buď začínáme procházku, nebo v něm končíme, případně obojí.

Je zřejmé, že existují nejvýše 2 úseky města druhého typu. Nemůžeme začít na dvou místech najednou, ani nemůžeme skončit na dvou místech najednou.

Jelikož existují čtyři úseky města, znamená to, že existují alespoň dva úseky města, v nichž naši procházku ani nekončíme, ani nezačínáme. Vyberme si jeden z nich.

Kdykoli do tohoto sektoru vstoupíme, vyčerpáme jeden most, a kdykoli jej opustíme, využijeme druhý. Ke každému sektoru je však připojen lichý počet mostů! To je rozpor. Abychom pochopili proč, připomeňme si, že každý sektor má buď 3 mosty, nebo je k němu připojeno 5 mostů.

Pokud jsme v sektoru jednou, můžeme využít pouze dva z jeho mostů. Pokud jsme v něm dvakrát, využijeme čtyři jeho mosty (nebo nám dojdou mosty, pokud by měl pouze tři mosty). Pokud jsme v něm třikrát, potřebovali bychom 6 mostů, které nemůžeme mít. Požadavek, abychom do sektoru města, který není naším výchozím ani koncovým bodem, vstupovali i vystupovali z něj, je tedy v rozporu s tím, že počet spojovacích mostů je pro každý sektor lichý.