Typy interpolace – výhody a nevýhody
Metody interpolace
Interpolace je proces, při kterém se pomocí bodů se známými hodnotami nebo výběrových bodů odhadují hodnoty v jiných neznámých bodech. Lze ji použít k předpovědi neznámých hodnot u jakýchkoli geografických bodových dat, jako jsou nadmořská výška, srážky, koncentrace chemických látek, hladiny hluku a podobně.
Níže jsou uvedeny dostupné metody interpolace.
Interpolátor vážený inverzní vzdáleností (IDW)
Interpolátor vážený inverzní vzdáleností předpokládá, že každý vstupní bod má lokální vliv, který se vzdáleností klesá. Bodům blíže k buňce zpracování přikládá větší váhu než bodům vzdálenějším. Pro určení výstupní hodnoty každého místa lze použít zadaný počet bodů nebo všechny body v zadaném poloměru. Použití této metody předpokládá, že vliv mapované proměnné klesá se vzdáleností od jejího vzorkovaného místa.
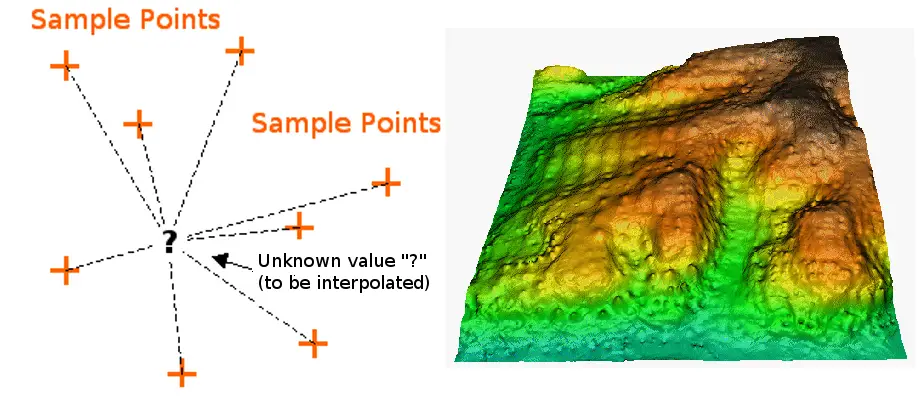
IDW Interpolace; s laskavým svolením: QGIS
Algoritmus IDW (Inverse Distance Weighting) je efektivně interpolátorem klouzavého průměru, který se obvykle používá pro velmi proměnlivá data. U některých typů dat je možné se vrátit na místo sběru a zaznamenat novou hodnotu, která se statisticky liší od původního údaje, ale je v rámci obecného trendu pro danou oblast.
Interpolovaná plocha odhadnutá technikou klouzavého průměru je menší než místní maximální hodnota a větší než místní minimální hodnota.

IDW interpolovaný povrch; S laskavým svolením:ESRI
IDW interpolace explicitně implementuje předpoklad, že věci, které jsou blízko sebe, jsou si podobnější než ty, které jsou od sebe dále. Pro predikci hodnoty pro libovolné neměřené místo použije IDW naměřené hodnoty v okolí predikovaného místa. Ty naměřené hodnoty, které jsou nejblíže předpovídanému místu, budou mít na předpovídanou hodnotu větší vliv než ty vzdálenější. IDW tedy předpokládá, že každý měřený bod má lokální vliv, který se vzdáleností klesá. Funkce IDW by se měla používat, pokud je množina bodů dostatečně hustá, aby zachytila rozsah lokálních změn povrchu potřebných pro analýzu. IDW určuje hodnoty buněk pomocí lineárně vážené kombinace množiny výběrových bodů. Bodům blíže k místu predikce dává větší váhu než bodům vzdálenějším, odtud název inverzní vážená vzdálenost.
Technika IDW vypočítá hodnotu pro každý uzel sítě zkoumáním okolních datových bodů, které leží v uživatelem definovaném poloměru hledání. Některé nebo všechny datové body mohou být použity v procesu interpolace. Hodnota uzlu se vypočítá zprůměrováním váženého součtu všech bodů. Datové body, které leží postupně dále od uzlu, ovlivňují vypočtenou hodnotu mnohem méně než ty, které leží blíže k uzlu.
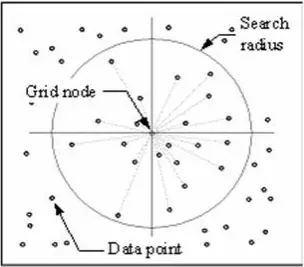
Okolo každého uzlu sítě se vytvoří poloměr, ze kterého se vyberou datové body, které se použijí při výpočtu. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Jde o další metodu váženého průměru, základní rovnice používaná při interpolaci přirozených sousedů je totožná s rovnicí používanou při interpolaci IDW. Tato metoda dokáže efektivně zpracovávat velké soubory vstupních bodových dat. Při použití metody přirozeného souseda určují místní souřadnice velikost vlivu, který bude mít kterýkoli bod rozptylu na výstupní buňky.
Metoda přirozeného souseda je geometrická technika odhadu, která využívá oblasti přirozeného sousedství vytvořené kolem každého bodu v datové sadě.
Stejně jako IDW je tato interpolační metoda metodou váženého průměru. Avšak namísto zjišťování hodnoty interpolovaného bodu pomocí všech vstupních bodů vážených jejich vzdáleností vytvoří interpolace Natural Neighbors Delauneyovu triangulaci vstupních bodů a vybere nejbližší uzly, které tvoří konvexní plášť kolem interpolačního bodu, a poté váží jejich hodnoty poměrnou plochou. Tato metoda je nejvhodnější tam, kde jsou body vzorku dat rozloženy s nerovnoměrnou hustotou. Je to dobrá univerzální interpolační technika a její výhodou je, že nemusíte zadávat parametry, jako je poloměr, počet sousedů nebo váhy.

Přírodní IDW: S laskavým svolením:
Tato technika je navržena tak, aby ctila lokální minimální a maximální hodnoty v bodovém souboru a lze ji nastavit tak, aby omezila překračování lokálních vysokých hodnot a podkračování lokálních nízkých hodnot. Metoda tak umožňuje vytvářet přesné modely povrchů ze souborů dat, které mají velmi řídké nebo velmi lineární prostorové rozložení.
Výhody
- Zpracovává efektivně velký počet bodů vzorku.
Spline
Spline odhaduje hodnoty pomocí matematické funkce, která minimalizuje celkové zakřivení povrchu, takže výsledkem je hladký povrch, který přesně prochází vstupními body.

Spline: S laskavým svolením: ESRI
Koncepčně se jedná o obdobu ohýbání gumového plátu tak, aby procházel známými body při minimalizaci celkového zakřivení povrchu. Přizpůsobí matematickou funkci zadanému počtu nejbližších vstupních bodů, přičemž prochází vzorovými body. Tato metoda je nejlepší pro jemně se měnící povrchy, jako je nadmořská výška, výška hladiny podzemní vody nebo koncentrace znečištění.
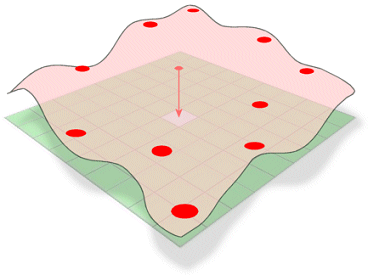
Metoda interpolace Spline odhaduje neznámé hodnoty ohýbáním povrchu přes známé hodnoty.
Existují dvě spline metody: regularizovaná a tahová.
Regularizovaná metoda vytváří hladký, postupně se měnící povrch s hodnotami, které mohou ležet mimo rozsah výběrových dat. Do svých minimalizačních výpočtů zahrnuje první derivaci (sklon), druhou derivaci (rychlost změny sklonu) a třetí derivaci (rychlost změny druhé derivace).
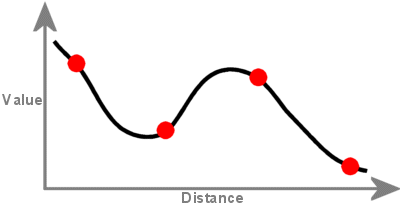
Povrch vytvořený pomocí interpolace Spline prochází každým bodem vzorku a může překročit rozsah hodnot sady bodů vzorku.
Ačkoli metoda Tension spline používá pouze první a druhou derivaci, zahrnuje do výpočtu Spline více bodů, což obvykle vytváří hladší povrchy, ale prodlužuje dobu výpočtu.
Tato metoda protahuje povrch přes získané body, což vede k efektu protažení. Spline používá k výpočtu hodnot buněk zakřivené čáry (metoda curvilinear Lines).
Výběr váhy pro interpolaci Spline
Regularizovaný spline: Čím vyšší je váha, tím hladší je povrch. Vhodné jsou váhy mezi 0 a 5. Typické hodnoty jsou 0, 0,001, 0,01, 0,1 a 0,5.
Napínací spline: Čím vyšší je váha, tím hrubší je povrch a hodnoty více odpovídají rozsahu dat vzorku. Hodnoty vah musí být větší nebo rovny nule. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Krigingový postup, který vytváří odhadovanou plochu z rozptýlené množiny bodů s hodnotami z. Kriging předpokládá, že vzdálenost nebo směr mezi body vzorku odráží prostorovou korelaci, kterou lze použít k vysvětlení variability povrchu. Nástroj Kriging fituje matematickou funkci na zadaný počet bodů nebo na všechny body v zadaném poloměru, aby určil výstupní hodnotu pro každé místo. Kriging je vícekrokový proces; zahrnuje průzkumnou statistickou analýzu dat, modelování variogramu, vytvoření povrchu a (volitelně) průzkum variančního povrchu. Kriging je nejvhodnější, pokud víte, že v datech existuje prostorově korelovaná vzdálenost nebo směrová odchylka. Často se používá v půdoznalství a geologii.
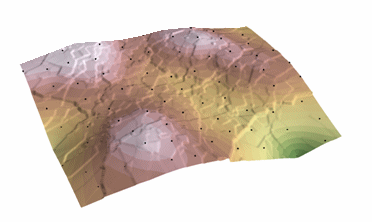
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
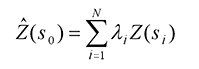
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. U metody kriging však váhy závisí nejen na vzdálenosti mezi měřenými body a místem předpovědi, ale také na celkovém prostorovém uspořádání měřených bodů. Aby bylo možné prostorové uspořádání ve vahách použít, je třeba kvantifikovat prostorovou autokorelaci. V běžném krigingu tedy váha λi závisí na přizpůsobeném modelu měřeným bodům, vzdálenosti k místu předpovědi a prostorových vztazích mezi naměřenými hodnotami v okolí místa předpovědi. Následující části pojednávají o tom, jak se obecný krigingový vzorec používá k vytvoření mapy předpovědní plochy a mapy přesnosti předpovědí.
Typy krigingu
Ordinární kriging
Ordinární kriging předpokládá model
Z(s) = µ + ε(s),
kde µ je neznámá konstanta. Jednou z hlavních otázek týkajících se obyčejného krigingu je, zda je předpoklad konstantní střední hodnoty rozumný. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indikátorové kriging
Indikátorové kriging předpokládá model
I(s) = µ + ε(s),
kde µ je neznámá konstanta a I(s) je binární proměnná. Vytvoření binárních dat může být pomocí prahové hodnoty pro spojitá data, nebo může jít o to, že pozorovaná data mají hodnotu 0 nebo 1. Například můžete mít vzorek, který se skládá z informace o tom, zda je bod lesním nebo nelesním stanovištěm, kde binární proměnná označuje příslušnost ke třídě. Při použití binárních proměnných postupuje indikační kriging stejně jako obyčejný kriging.
Indikační kriging může používat buď semivariogramy, nebo kovariance.
Pravděpodobnostní kriging
Pravděpodobnostní kriging předpokládá model
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
kde µ1 a µ2 jsou neznámé konstanty a I(s) je binární proměnná vytvořená pomocí prahového indikátoru, I(Z(s) > ct). Všimněte si, že nyní existují dva typy náhodných chyb, ε1(s) a ε2(s), takže pro každou z nich existuje autokorelace a křížová korelace mezi nimi. Pravděpodobnostní kriging se snaží o totéž co indikátorový kriging, ale ve snaze odvést lepší práci používá cokriging.
Pravděpodobnostní kriging může používat buď semivariogramy, nebo kovariance, křížové kovariance a transformace, ale nemůže zohlednit chybu měření.
style=“display:inline-block;width:468px;height:60px“ data-ad-client=“ca-pub-7134201556760050″ data-ad-slot=“9271753327″>
Disjunktivní kriging
Disjunktivní kriging vychází z předpokladu, že se jedná o model
f(Z(s)) = µ1 + ε(s),
kde µ1 je neznámá konstanta a f(Z(s)) je libovolná funkce Z(s). Všimněte si, že můžete psát f(Z(s)) = I(Z(s) > ct), takže indikační kriging je speciálním případem disjunktního krigingu. V programu Geostatistical Analyst můžete pomocí disjunktního krigingu předpovídat buď samotnou hodnotu, nebo indikátor.
Disjunktivní kriging se obecně snaží dělat více než běžný kriging. Odměny mohou být sice větší, ale také náklady. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Chcete-li získat hlubší vhled do matematického přístupu ke krigingu, klikněte na položku Kriging a metoda interpolace.
PointInterp
Metoda, která je podobná IDW, funkce PointInterp umožňuje větší kontrolu nad okolím vzorkování. Vliv konkrétního vzorku na hodnotu interpolované buňky mřížky závisí na tom, zda se bod vzorku nachází v sousedství buňkyʼ a jak daleko od interpolované buňky se nachází. Body mimo okolí nemají žádný vliv.

PointInterp; Courtesy: ESRI
Vážená hodnota bodů uvnitř sousedství se vypočítá pomocí inverzní interpolace vážené vzdálenosti nebo inverzní exponenciální interpolace vzdálenosti. Tato metoda interpoluje rastr pomocí bodových prvků, ale umožňuje různé typy sousedství. Okolí mohou mít tvar kruhů, obdélníků, nepravidelných mnohoúhelníků, anulů nebo klínů.
Trend
Trend je statistická metoda, která najde povrch, který vyhovuje bodům vzorku pomocí regresního fitování metodou nejmenších čtverců. Na celý povrch se hodí jedna polynomická rovnice. Výsledkem je povrch, který minimalizuje rozptyl povrchu ve vztahu ke vstupním hodnotám. Povrch je konstruován tak, aby pro každý vstupní bod byl součet rozdílů mezi skutečnými a odhadovanými hodnotami (tj. rozptyl) co nejmenší.

Trend; Courtsey:ESRI
Jedná se o nepřesný interpolátor a výsledný povrch zřídka prochází vstupními body. Tato metoda však zjišťuje trendy v datech vzorku a je podobná přírodním jevům, které se obvykle mění plynule.
Výhody
- Trendové povrchy jsou vhodné pro identifikaci vzorců v hrubém měřítku v datech; interpolovaný povrch zřídka prochází body vzorku.
Topo to Raster
Metoda Topo to Raster interpolací výškových hodnot pro rastr zavádí omezení, která zajišťují hydrologicky správný digitální výškový model, který obsahuje propojenou strukturu odvodnění a správně reprezentuje hřebeny a toky ze vstupních vrstevnicových dat. Používá iterační techniku interpolace s konečným rozdílem, která optimalizuje výpočetní účinnost lokální interpolace, aniž by se ztratila povrchová spojitost globální interpolace. Byl speciálně navržen pro inteligentní práci s obrysovými vstupy.
Níže je příklad povrchu interpolovaného z výškových bodů, vrstevnic, linií potoků a polygonů jezer pomocí interpolace Topo to Raster.
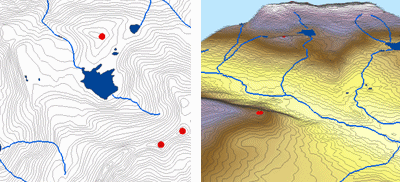
Topo to raster; Courtesy: ESRI
Topo to Raster je specializovaný nástroj pro vytváření hydrologicky korektních rastrových povrchů z vektorových dat terénních komponent, jako jsou výškové body, vrstevnice, linie toků, polygony jezer, ponorné body a polygony hranic studované oblasti.
Hustota
Nástroje hustoty (dostupné v ArcGIS) vytvářejí povrch, který vyjadřuje, kolik nebo kolik nějaké věci připadá na jednotku plochy. Nástroj Hustota je užitečný pro vytváření povrchů hustoty, které reprezentují rozložení populace volně žijících živočichů na základě souboru pozorování nebo stupeň urbanizace oblasti na základě hustoty silnic.

Density Raster; Courtest: ERSI
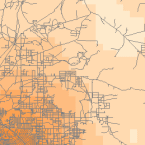
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method