Vennovy diagramy
Chris Joyce (2008)
Vennův diagram je typ grafického organizéru. Grafické organizátory představují způsob vizuálního uspořádání složitých vztahů. Umožňují zviditelnit abstraktní myšlenky.
Ačkoli jsou Vennovy diagramy především nástrojem myšlení, lze je použít i pro hodnocení. Než je však lze takto použít, musí se s nimi žáci již seznámit.
Kdy je použít
Vennovy diagramy se používají k porovnávání a porovnávání skupin věcí.
Jsou užitečným nástrojem formativního hodnocení, protože:
-
mohou být použity k vyvolání diskuse; a
- poskytují učitelům informace o myšlení žáků.
V přírodních vědách jsou užitečné při klasifikaci.
Jako uznávaná konvence pro znázornění podobností a rozdílů přispívá znalost jejich používání ke klíčové kompetenci Používání jazyka, symbolů a textů.
Teorie
Vennovy diagramy pocházejí z odvětví matematiky, které se nazývá teorie množin. John Venn je vyvinul v roce 1891 k zobrazení vztahů mezi množinami. Nyní se používají v mnoha dalších oborech.
Informace jsou studentům obvykle předkládány v lineárním textu. Zejména při velkém množství informací je v tomto formátu obtížné vidět vztahy. Vennovy diagramy umožňují studentům vizuálně uspořádat informace tak, aby byli schopni vidět vztahy mezi dvěma nebo třemi soubory položek. Mohou pak identifikovat podobnosti a rozdíly.
Jak strategie funguje
Vennův diagram se skládá z překrývajících se kruhů. Každý kruh obsahuje všechny prvky množiny. Místa, kde se kruhy překrývají, ukazují prvky, které má množina společné. Generally there are two or three circles. Any more and the exercise becomes very complicated.
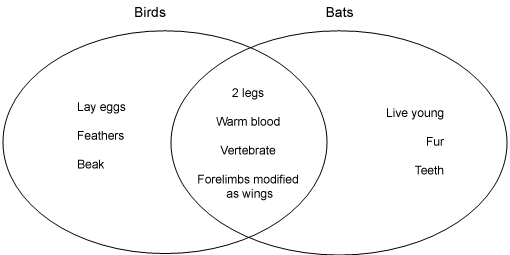
The following science example compares the features of bats and birds.
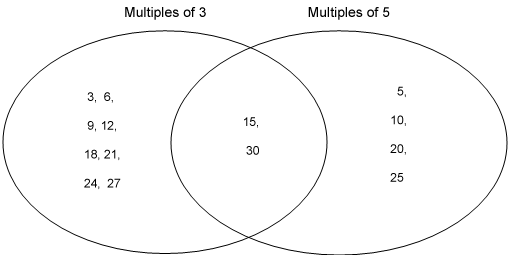
The following is a maths example:
What to do
Creating a Venn diagram
If the assessment focus is on organising information:
-
Students view written text, pictures, diagrams, or video/film about two (or sometimes three) items that have some related characteristics.
-
Identify what items they want to compare (e.g., birds and bats).*
-
Draw two overlapping circles. Label each circle (Bird, Bat).
-
In each circle, fill in the characteristics of each item.
-
Identify which characteristics appear in both circles. Tyto charakteristiky patří do průsečíku (tam, kde se oba kruhy překrývají).
-
Někdy jsou zahrnuty i charakteristiky, které se nevejdou ani do jedné sady. Např. v příkladu s matematikou, pokud by byla zahrnuta všechna čísla od 1 do 30, některá by nebyla násobkem ani 3, ani 5. V případě, že by byla zahrnuta všechna čísla od 1 do 30, některá by nebyla násobkem ani 3, ani 5. Ty jsou umístěny mimo kruhy.
Je vhodnější, aby studenti následně použili svůj Vennův diagram k porovnání množin.
*Někdy je prvním krokem nakreslení obdélníku a určení univerzální množiny. Například ve výše uvedeném přírodovědném příkladu mohou být univerzální množinou Zvířata, která létají. Uvnitř obdélníku se pak nakreslí kruhy pro ptáky a netopýry.
Čtení Vennova diagramu
Pokud je hodnocení zaměřeno na interpretaci Vennova diagramu:
-
Pokládejte otázky týkající se podobností a rozdílů, které Vennův diagram znázorňuje.
-
Uveďte pravdivá/nepravdivá tvrzení, např. 10 je násobkem 3 a 5.
-
Pokládejte otázky týkající se obou množin nebo o nich diskutujte. Studenti mohou být například schopni říci, že netopýři mají některé podobnosti s ptáky, ale nejsou to ptáci, protože nekladou vejce a nemají peří.
-
Pokud je to vhodné, pokládejte otázky, které studenty podněcují k zobecňování, např. můžeme netopýra zařadit do čeledi ptačí?
Omezení
Při zkoušení zdrojů ARB jsme zjistili, že mnoho studentů Vennovy diagramy nepoužívá dobře. Někteří je neznají. Pokud Vennovy diagramy používáte jako strategii hodnocení, musí studenti již prokázat, že vědí, jak fungují, aby bylo hodnocení validní.
Přizpůsobení strategie
- Vennovy diagramy jsou široce používány jako nástroj myšlení. Jsou proto také užitečnou výukovou strategií.
- Mohou být užitečné pro procvičování tvorby logických tvrzení, např. pokud/tedy, vše/něco/ne, může být.
- Při výuce žáků o Vennových diagramech nebo při práci s mladšími žáky používejte konkrétní materiály, např. lístečky, kartičky, provázek nebo obruče, kterými mohou žáci pohybovat.
- Počítačové programy, jako je Inspiration, jsou užitečné pro vytváření Vennových diagramů.