Wellenlänge
In linearen Medien kann jedes Wellenmuster durch die unabhängige Ausbreitung sinusförmiger Komponenten beschrieben werden. Die Wellenlänge λ einer sinusförmigen Wellenform, die sich mit konstanter Geschwindigkeit v ausbreitet, ist gegeben durch
λ = v f , {\displaystyle \lambda ={\frac {v}{f}}\,\,,}

wobei v die Phasengeschwindigkeit (Betrag der Phasengeschwindigkeit) der Welle und f die Frequenz der Welle ist. In einem dispersiven Medium hängt die Phasengeschwindigkeit selbst von der Frequenz der Welle ab, so dass die Beziehung zwischen Wellenlänge und Frequenz nichtlinear ist.
Im Fall von elektromagnetischer Strahlung – wie Licht – im freien Raum entspricht die Phasengeschwindigkeit der Lichtgeschwindigkeit, etwa 3×108 m/s. Die Wellenlänge einer elektromagnetischen (Radio-)Welle von 100 MHz ist also etwa: 3×108 m/s geteilt durch 108 Hz = 3 Meter. Die Wellenlänge des sichtbaren Lichts reicht von tiefrot, etwa 700 nm, bis violett, etwa 400 nm (weitere Beispiele siehe elektromagnetisches Spektrum).
Für Schallwellen in der Luft beträgt die Schallgeschwindigkeit 343 m/s (bei Raumtemperatur und atmosphärischem Druck). Die Wellenlängen der für das menschliche Ohr hörbaren Schallfrequenzen (20 Hz-20 kHz) liegen also zwischen etwa 17 m und 17 mm. Fledermäuse verwenden etwas höhere Frequenzen, damit sie Ziele, die kleiner als 17 mm sind, auflösen können. Die Wellenlängen des hörbaren Schalls sind viel länger als die des sichtbaren Lichts.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Wenn der Kasten beispielsweise ideale Metallwände hat, ergibt sich für eine elektromagnetische Welle die Bedingung für Knoten an den Wänden, weil die Metallwände kein tangentiales elektrisches Feld tragen können, was die Welle zwingt, an der Wand eine Amplitude von Null zu haben.
Die stehende Welle kann als Summe von zwei sich ausbreitenden Sinuswellen mit entgegengesetzten Geschwindigkeiten betrachtet werden. Folglich stehen Wellenlänge, Periode und Wellengeschwindigkeit in der gleichen Beziehung wie bei einer sich ausbreitenden Welle. So lässt sich beispielsweise die Lichtgeschwindigkeit aus der Beobachtung stehender Wellen in einem Metallkasten, der ein ideales Vakuum enthält, bestimmen.
Mathematische DarstellungBearbeiten
Wandernde Sinuswellen werden häufig mathematisch in Form ihrer Geschwindigkeit v (in x-Richtung), ihrer Frequenz f und ihrer Wellenlänge λ dargestellt als:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}

wobei y der Wert der Welle an einer beliebigen Position x und Zeit t und A die Amplitude der Welle ist. Sie werden auch üblicherweise in Form der Wellenzahl k (2π-facher Kehrwert der Wellenlänge) und der Winkelfrequenz ω (2π-fache Frequenz) ausgedrückt als:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}

wobei Wellenlänge und Wellenzahl mit der Geschwindigkeit und der Frequenz wie folgt zusammenhängen:
k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},}

oder
λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.}

In der zweiten oben genannten Form wird die Phase (kx – ωt) oft zu (k-r – ωt) verallgemeinert, indem die Wellenzahl k durch einen Wellenvektor ersetzt wird, der die Richtung und die Wellenzahl einer ebenen Welle im 3-Raum angibt, die durch den Ortsvektor r parametrisiert ist. In diesem Fall steht die Wellenzahl k, der Betrag von k, immer noch in der gleichen Beziehung zur Wellenlänge wie oben gezeigt, wobei v als skalare Geschwindigkeit in Richtung des Wellenvektors interpretiert wird. Die erste Form, bei der die reziproke Wellenlänge in der Phase verwendet wird, lässt sich nicht so leicht auf eine Welle in einer beliebigen Richtung verallgemeinern.
Verallgemeinerungen auf Sinuskurven mit anderen Phasen und auf komplexe Exponentiale sind ebenfalls üblich; siehe ebene Welle. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. Insbesondere ist die Lichtgeschwindigkeit in einem Medium geringer als im Vakuum, was bedeutet, dass dieselbe Frequenz im Medium einer kürzeren Wellenlänge entspricht als im Vakuum, wie in der Abbildung rechts dargestellt.
Diese Änderung der Geschwindigkeit beim Eintritt in ein Medium bewirkt eine Brechung oder eine Richtungsänderung von Wellen, die in einem Winkel auf die Grenzfläche zwischen Medien treffen. Für elektromagnetische Wellen wird diese Änderung des Ausbreitungswinkels durch das Snellsche Gesetz bestimmt.
Die Wellengeschwindigkeit in einem Medium kann sich nicht nur von der in einem anderen unterscheiden, sondern die Geschwindigkeit variiert typischerweise mit der Wellenlänge. Folglich ändert sich die Richtungsänderung beim Eintritt in ein anderes Medium mit der Wellenlänge der Welle.
Für elektromagnetische Wellen wird die Geschwindigkeit in einem Medium durch seinen Brechungsindex gemäß
v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},}

wobei c die Lichtgeschwindigkeit im Vakuum und n(λ0) der Brechungsindex des Mediums bei der Wellenlänge λ0 ist, wobei letzterer im Vakuum und nicht im Medium gemessen wird. Die entsprechende Wellenlänge im Medium ist
λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}

Wenn Wellenlängen von elektromagnetischer Strahlung angegeben werden, ist in der Regel die Wellenlänge im Vakuum gemeint, es sei denn, die Wellenlänge wird ausdrücklich als die Wellenlänge in einem anderen Medium bezeichnet. In der Akustik, wo ein Medium für die Existenz der Wellen unerlässlich ist, wird der Wellenlängenwert für ein bestimmtes Medium angegeben.
Die Veränderung der Lichtgeschwindigkeit mit der Wellenlänge wird als Dispersion bezeichnet und ist auch für das bekannte Phänomen verantwortlich, bei dem Licht durch ein Prisma in die einzelnen Farben getrennt wird. Die Trennung erfolgt, wenn der Brechungsindex im Inneren des Prismas mit der Wellenlänge variiert, so dass sich verschiedene Wellenlängen mit unterschiedlichen Geschwindigkeiten im Prisma ausbreiten und in unterschiedlichen Winkeln gebrochen werden. Die mathematische Beziehung, die beschreibt, wie die Geschwindigkeit des Lichts in einem Medium mit der Wellenlänge variiert, wird als Dispersionsrelation bezeichnet.
Uneinheitliche MedienBearbeiten

Die Wellenlänge kann ein nützliches Konzept sein, selbst wenn die Welle nicht periodisch im Raum ist. Bei einer Meereswelle, die sich dem Ufer nähert, wie in der Abbildung dargestellt, schwankt die eintreffende Welle mit einer unterschiedlichen lokalen Wellenlänge, die zum Teil von der Tiefe des Meeresbodens im Vergleich zur Wellenhöhe abhängt. Die Analyse der Welle kann auf dem Vergleich der lokalen Wellenlänge mit der lokalen Wassertiefe beruhen.

Wellen, die zeitlich sinusförmig sind, sich aber durch ein Medium ausbreiten, dessen Eigenschaften mit der Position variieren (ein inhomogenes Medium), können sich mit einer Geschwindigkeit ausbreiten, die mit der Position variiert, und sind daher möglicherweise nicht sinusförmig im Raum. Die Abbildung rechts zeigt ein Beispiel. Wenn sich die Welle verlangsamt, wird die Wellenlänge kürzer und die Amplitude nimmt zu; nach einem Ort maximaler Reaktion ist die kurze Wellenlänge mit einem hohen Verlust verbunden und die Welle stirbt aus.
Die Analyse der Differentialgleichungen solcher Systeme erfolgt häufig näherungsweise mit der WKB-Methode (auch bekannt als Liouville-Green-Methode). Bei dieser Methode wird die Phase durch den Raum integriert, wobei eine lokale Wellenzahl verwendet wird, die als „lokale Wellenlänge“ der Lösung in Abhängigkeit von Zeit und Raum interpretiert werden kann.
Bei dieser Methode wird das System lokal so behandelt, als ob es mit den lokalen Eigenschaften gleichförmig wäre; insbesondere ist die mit einer Frequenz verbundene lokale Wellengeschwindigkeit das Einzige, was benötigt wird, um die entsprechende lokale Wellenzahl oder Wellenlänge zu schätzen. Darüber hinaus berechnet die Methode eine sich langsam ändernde Amplitude, um andere Bedingungen der Gleichungen oder des physikalischen Systems zu erfüllen, wie z. B. die Erhaltung der Energie in der Welle.
CrystalsEdit
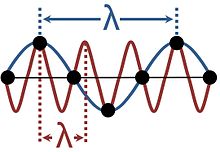
Wellen in kristallinen Festkörpern sind nicht kontinuierlich, da sie aus den Schwingungen diskreter Teilchen bestehen, die in einem regelmäßigen Gitter angeordnet sind. Dies führt zu Aliasing, da ein und dieselbe Schwingung eine Vielzahl unterschiedlicher Wellenlängen haben kann, wie in der Abbildung dargestellt. Beschreibungen, die mehr als eine dieser Wellenlängen verwenden, sind redundant; es ist üblich, die längste Wellenlänge zu wählen, die dem Phänomen entspricht. Der Wellenlängenbereich, der ausreicht, um alle möglichen Wellen in einem kristallinen Medium zu beschreiben, entspricht den Wellenvektoren, die auf die Brillouin-Zone beschränkt sind.
Diese Unbestimmtheit der Wellenlänge in Festkörpern ist wichtig für die Analyse von Wellenphänomenen wie Energiebändern und Gitterschwingungen. Sie ist mathematisch äquivalent zum Aliasing eines Signals, das in diskreten Intervallen abgetastet wird.