Våglängd

I linjära medier kan alla vågmönster beskrivas i termer av oberoende utbredning av sinusformade komponenter. Våglängden λ för en sinusformad vågform som rör sig med konstant hastighet v ges av

λ = v f , {\displaystyle \lambda ={\frac {v}{f}}}\,\,,}

där v kallas vågens fashastighet (storleken på fashastigheten) och f är vågens frekvens. I ett dispersivt medium beror själva fashastigheten på vågens frekvens, vilket gör förhållandet mellan våglängd och frekvens olinjärt.

I fallet med elektromagnetisk strålning – t.ex. ljus – i fri rymd är fashastigheten ljusets hastighet, ca 3×108 m/s. Våglängden för en elektromagnetisk (radio-)våg på 100 MHz är således ca: 3×108 m/s dividerat med 108 Hz = 3 meter. Våglängden för synligt ljus sträcker sig från djuprött, cirka 700 nm, till violett, cirka 400 nm (för andra exempel, se elektromagnetiskt spektrum).

För ljudvågor i luft är ljudets hastighet 343 m/s (vid rumstemperatur och atmosfäriskt tryck). Våglängderna för ljudfrekvenser som är hörbara för det mänskliga örat (20 Hz-20 kHz) ligger således mellan cirka 17 m respektive 17 mm. Fladdermöss använder något högre frekvenser för att kunna se mål som är mindre än 17 mm. Våglängder i hörbart ljud är mycket längre än i synligt ljus.

Sinusformade stående vågor i en låda som begränsar ändpunkterna till att vara noder kommer att ha ett heltal antal halva våglängder som passar i lådan.

A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue)

Standing wavesEdit

A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.

The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. För en elektromagnetisk våg till exempel, om lådan har ideala metallväggar, uppstår villkoret för noder vid väggarna eftersom metallväggarna inte kan stödja ett tangentiellt elektriskt fält, vilket tvingar vågen att ha nollamplitud vid väggen.

Den stationära vågen kan ses som summan av två rörliga sinusformade vågor med motsatta hastigheter. Följaktligen är våglängd, period och våghastighet relaterade precis som för en rörlig våg. Till exempel kan ljusets hastighet bestämmas genom observation av stående vågor i en metallåda som innehåller ett idealt vakuum.

Matematisk representationRedigera

Rörliga sinusformade vågor representeras ofta matematiskt i termer av deras hastighet v (i x-riktningen), frekvens f och våglängd λ som:

y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ). {\displaystyle y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}

där y är vågens värde vid varje position x och tid t och A är vågens amplitud. De uttrycks också vanligen i termer av vågtal k (2π gånger reciproken av våglängden) och vinkelfrekvens ω (2π gånger frekvensen) som:

y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}

där våglängd och vågtal är relaterade till hastighet och frekvens som:

k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},}

eller

λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}}.}

I den andra formen ovan generaliseras ofta fasen (kx – ωt) till (k-r – ωt), genom att vågtalet k ersätts med en vågvektor som anger riktningen och vågtalet för en plan våg i 3-rummet, parametrerad av positionsvektorn r. I det fallet står vågtalet k, storleken på k, fortfarande i samma förhållande till våglängden som visas ovan, där v tolkas som skalärhastighet i vågvektorns riktning. Den första formen, som använder reciprok våglängd i fasen, generaliseras inte lika lätt till en våg i en godtycklig riktning.

Generaliseringar till sinusoider med andra faser, och till komplexa exponentialer, är också vanliga; se plan våg. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave

A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit

Wavelength is decreased in a medium with slower propagation.

Refraction: upon entering a medium where its speed is lower, the wave changes direction.

Separation of colors by a prism (click for animation)

The speed of a wave depends upon the medium in which it propagates. I synnerhet är ljusets hastighet i ett medium lägre än i vakuum, vilket innebär att samma frekvens kommer att motsvara en kortare våglängd i mediet än i vakuum, vilket visas i figuren till höger.

Denna hastighetsförändring vid inträde i ett medium orsakar refraktion, eller en förändring av riktningen för vågor som möter gränssnittet mellan medier i en vinkel. För elektromagnetiska vågor styrs denna förändring i utbredningsvinkeln av Snells lag.

Våghastigheten i ett medium kan inte bara skilja sig från hastigheten i ett annat medium, utan hastigheten varierar vanligtvis med våglängden. Följaktligen ändras riktningsförändringen vid inträde i ett annat medium med vågens våglängd.

För elektromagnetiska vågor styrs hastigheten i ett medium av dess brytningsindex enligt

v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},}

där c är ljusets hastighet i vakuum och n(λ0) är mediets brytningsindex vid våglängden λ0, där det senare mäts i vakuum snarare än i mediet. Motsvarande våglängd i mediet är

λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}

När våglängder för elektromagnetisk strålning anges avses vanligen våglängden i vakuum, såvida inte våglängden särskilt anges som våglängden i något annat medium. I akustik, där ett medium är nödvändigt för att vågorna ska existera, anges våglängdsvärdet för ett specificerat medium.

Variationen i ljusets hastighet med våglängden kallas dispersion och är också ansvarig för det välkända fenomenet där ljuset separeras i beståndsdelar i färgerna genom ett prisma. Separationen sker när brytningsindexet inuti prismat varierar med våglängden, så att olika våglängder fortplantar sig med olika hastighet inuti prismat, vilket gör att de bryts i olika vinklar. Det matematiska förhållandet som beskriver hur ljusets hastighet i ett medium varierar med våglängden kallas för en dispersionsrelation.

Oenhetliga medierRedigera

Olika lokala våglängder på en krön-till-krön-basis i en havsvåg som närmar sig stranden

Våglängden kan vara ett användbart begrepp även om vågen inte är periodisk i rummet. Till exempel, i en havsvåg som närmar sig kusten, som visas i figuren, böljar den inkommande vågen med en varierande lokal våglängd som delvis beror på havsbottnens djup i förhållande till våghöjden. Analysen av vågen kan baseras på en jämförelse mellan den lokala våglängden och det lokala vattendjupet.

En sinusformad våg som färdas i ett ojämnt medium, med förlust

Vågor som är sinusformade i tid men som fortplantar sig genom ett medium vars egenskaper varierar med positionen (ett inhomogent medium) kan fortplanta sig med en hastighet som varierar med positionen, och som ett resultat av detta kan de inte vara sinusformade i rummet. Figuren till höger visar ett exempel. När vågen saktar ner blir våglängden kortare och amplituden ökar; efter en plats med maximal respons är den korta våglängden förknippad med en hög förlust och vågen dör ut.

Analysen av differentialekvationer för sådana system görs ofta approximativt, med hjälp av WKB-metoden (även känd som Liouville-Green-metoden). Metoden integrerar fas genom rummet med hjälp av ett lokalt vågtal, vilket kan tolkas som att det anger en ”lokal våglängd” för lösningen som funktion av tid och rum. metoden behandlar systemet lokalt som om det vore enhetligt med de lokala egenskaperna; i synnerhet är den lokala våghastigheten i samband med en frekvens det enda som behövs för att uppskatta motsvarande lokala vågtal eller våglängd. Dessutom beräknar metoden en långsamt föränderlig amplitud för att uppfylla andra begränsningar i ekvationerna eller i det fysiska systemet, t.ex. för bevarandet av energin i vågen.

CrystalsEdit

En våg på en rad av atomer kan tolkas enligt en mängd olika våglängder.

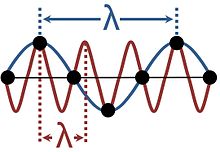
Vågor i kristallina fasta ämnen är inte kontinuerliga, eftersom de består av vibrationer hos diskreta partiklar som är arrangerade i ett regelbundet gitter. Detta ger aliasing eftersom samma vibration kan anses ha en mängd olika våglängder, vilket visas i figuren. Beskrivningar som använder mer än en av dessa våglängder är överflödiga; det är konventionellt att välja den längsta våglängden som passar fenomenet. Det intervall av våglängder som är tillräckligt för att ge en beskrivning av alla möjliga vågor i ett kristallint medium motsvarar de vågvektorer som är begränsade till Brillouin-zonen.

Denna obestämdhet i våglängder i fasta ämnen är viktig vid analysen av vågfenomen som energiband och gittervibrationer. Den är matematiskt likvärdig med aliasing av en signal som samplats med diskreta intervaller.