Longitud de onda
En medios lineales, cualquier patrón de onda puede describirse en términos de la propagación independiente de componentes sinusoidales. La longitud de onda λ de una forma de onda sinusoidal que viaja a velocidad constante v viene dada por
λ = v f , {\displaystyle \lambda ={frac {v}{f}},\},

donde v se llama la velocidad de fase (magnitud de la velocidad de fase) de la onda y f es la frecuencia de la onda. En un medio dispersivo, la propia velocidad de fase depende de la frecuencia de la onda, lo que hace que la relación entre la longitud de onda y la frecuencia no sea lineal.
En el caso de la radiación electromagnética -como la luz- en el espacio libre, la velocidad de fase es la velocidad de la luz, unos 3×108 m/s. Por lo tanto, la longitud de onda de una onda electromagnética (radio) de 100 MHz es aproximadamente: 3×108 m/s dividido por 108 Hz = 3 metros. La longitud de onda de la luz visible va desde el rojo intenso, aproximadamente 700 nm, hasta el violeta, aproximadamente 400 nm (para otros ejemplos, véase el espectro electromagnético).
Para las ondas sonoras en el aire, la velocidad del sonido es de 343 m/s (a temperatura ambiente y presión atmosférica). Por tanto, las longitudes de onda de las frecuencias sonoras audibles para el oído humano (20 Hz-20 kHz) se sitúan aproximadamente entre 17 m y 17 mm, respectivamente. Los murciélagos utilizan frecuencias algo más altas para poder resolver objetivos menores de 17 mm. Las longitudes de onda en el sonido audible son mucho más largas que las de la luz visible.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Por ejemplo, para una onda electromagnética, si la caja tiene paredes metálicas ideales, la condición de los nodos en las paredes resulta porque las paredes metálicas no pueden soportar un campo eléctrico tangencial, lo que obliga a la onda a tener amplitud cero en la pared.
La onda estacionaria puede verse como la suma de dos ondas sinusoidales viajeras de velocidades opuestas. En consecuencia, la longitud de onda, el periodo y la velocidad de la onda están relacionados igual que para una onda viajera. Por ejemplo, la velocidad de la luz puede determinarse a partir de la observación de las ondas estacionarias en una caja metálica que contenga un vacío ideal.
Representación matemáticaEditar
Las ondas sinusoidales viajeras suelen representarse matemáticamente en términos de su velocidad v (en la dirección x), frecuencia f y longitud de onda λ como:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ) {\displaystyle y(x,\ t)=Acos \left(2\pi \left({\frac {x}{lambda }}-ft\right)\right)=Acos \left({\frac {2\pi }{lambda }}(x-vt)\right)}

donde y es el valor de la onda en cualquier posición x y tiempo t, y A es la amplitud de la onda. También se suelen expresar en términos del número de onda k (2π veces el recíproco de la longitud de onda) y la frecuencia angular ω (2π veces la frecuencia) como:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}

en la que la longitud de onda y el número de onda están relacionados con la velocidad y la frecuencia como:
k = 2 π λ = 2 π f v = ω v , {\displaystyle k={{frac {2\pi }{lambda }}={frac {2\pi f}{v}}={frac {\omega }{v},

o
λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={frac {2\pi }{k}={frac {2\pi v}{\omega }}={frac {v}{f}.}

En la segunda forma dada anteriormente, la fase (kx – ωt) se suele generalizar a (k-r – ωt), sustituyendo el número de onda k por un vector de onda que especifica la dirección y el número de onda de una onda plana en el espacio 3, parametrizada por el vector de posición r. En ese caso, el número de onda k, la magnitud de k, sigue estando en la misma relación con la longitud de onda que la mostrada anteriormente, y v se interpreta como la velocidad escalar en la dirección del vector de onda. La primera forma, utilizando la longitud de onda recíproca en la fase, no se generaliza tan fácilmente a una onda en una dirección arbitraria.
También son comunes las generalizaciones a sinusoides de otras fases, y a exponenciales complejas; véase onda plana. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. En particular, la velocidad de la luz en un medio es menor que en el vacío, lo que significa que la misma frecuencia corresponderá a una longitud de onda más corta en el medio que en el vacío, como se muestra en la figura de la derecha.
Este cambio de velocidad al entrar en un medio provoca la refracción, o el cambio de dirección de las ondas que encuentran la interfaz entre medios en un ángulo. En el caso de las ondas electromagnéticas, este cambio en el ángulo de propagación se rige por la ley de Snell.
La velocidad de las ondas en un medio no sólo puede diferir de la de otro, sino que la velocidad suele variar con la longitud de onda. Como resultado, el cambio de dirección al entrar en un medio diferente cambia con la longitud de onda de la onda.
Para las ondas electromagnéticas la velocidad en un medio se rige por su índice de refracción según
v = c n ( λ 0 ) , {\displaystyle v={frac {c}{n(\lambda _{0})},}

donde c es la velocidad de la luz en el vacío y n(λ0) es el índice de refracción del medio a la longitud de onda λ0, donde esta última se mide en el vacío y no en el medio. La longitud de onda correspondiente en el medio es
λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={frac {\lambda _{0}}{n(\lambda _{0})}}.

Cuando se citan las longitudes de onda de la radiación electromagnética, normalmente se habla de la longitud de onda en el vacío, a menos que la longitud de onda se identifique específicamente como la longitud de onda en algún otro medio. En acústica, donde un medio es esencial para que las ondas existan, el valor de la longitud de onda se da para un medio específico.
La variación de la velocidad de la luz con la longitud de onda se conoce como dispersión, y también es responsable del conocido fenómeno en el que la luz se separa en los colores componentes por un prisma. La separación se produce cuando el índice de refracción en el interior del prisma varía con la longitud de onda, por lo que las diferentes longitudes de onda se propagan a diferentes velocidades en el interior del prisma, haciendo que se refracten en diferentes ángulos. La relación matemática que describe cómo varía la velocidad de la luz dentro de un medio con la longitud de onda se conoce como relación de dispersión.
Medios no uniformesEditar

La longitud de onda puede ser un concepto útil incluso si la ola no es periódica en el espacio. Por ejemplo, en una ola oceánica que se acerca a la costa, mostrada en la figura, la ola entrante ondula con una longitud de onda local variable que depende en parte de la profundidad del fondo marino en comparación con la altura de la ola. El análisis de la ola puede basarse en la comparación de la longitud de onda local con la profundidad local del agua.

Las ondas que son sinusoidales en el tiempo pero que se propagan a través de un medio cuyas propiedades varían con la posición (un medio no homogéneo) pueden propagarse a una velocidad que varía con la posición, y como resultado pueden no ser sinusoidales en el espacio. La figura de la derecha muestra un ejemplo. A medida que la onda se ralentiza, la longitud de onda se acorta y la amplitud aumenta; después de un lugar de máxima respuesta, la longitud de onda corta se asocia con una pérdida elevada y la onda se extingue.
El análisis de las ecuaciones diferenciales de tales sistemas suele hacerse de forma aproximada, utilizando el método WKB (también conocido como método de Liouville-Green). El método integra la fase a través del espacio utilizando un número de onda local, que puede interpretarse como la indicación de una «longitud de onda local» de la solución en función del tiempo y el espacio.Este método trata el sistema localmente como si fuera uniforme con las propiedades locales; en particular, la velocidad de onda local asociada a una frecuencia es lo único que se necesita para estimar el correspondiente número de onda local o longitud de onda. Además, el método calcula una amplitud que cambia lentamente para satisfacer otras restricciones de las ecuaciones o del sistema físico, como para la conservación de la energía en la onda.
CristalesEdit
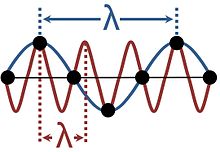
Las ondas en los sólidos cristalinos no son continuas, porque están compuestas por vibraciones de partículas discretas dispuestas en una red regular. Esto produce aliasing porque se puede considerar que la misma vibración tiene una variedad de longitudes de onda diferentes, como se muestra en la figura. Las descripciones que utilizan más de una de estas longitudes de onda son redundantes; lo convencional es elegir la longitud de onda más larga que se ajuste al fenómeno. El rango de longitudes de onda suficiente para proporcionar una descripción de todas las ondas posibles en un medio cristalino corresponde a los vectores de onda confinados en la zona de Brillouin.
Esta indeterminación en la longitud de onda en los sólidos es importante en el análisis de los fenómenos ondulatorios como las bandas de energía y las vibraciones de la red. Es matemáticamente equivalente al aliasing de una señal que se muestrea a intervalos discretos.