Longueur d’onde
Dans les milieux linéaires, toute forme d’onde peut être décrite en termes de propagation indépendante de composantes sinusoïdales. La longueur d’onde λ d’une onde sinusoïdale se déplaçant à vitesse constante v est donnée par
λ = v f , {\displaystyle \lambda ={\frac {v}{f}}\,\,,}

où v est appelée la vitesse de phase (grandeur de la vitesse de phase) de l’onde et f est la fréquence de l’onde. Dans un milieu dispersif, la vitesse de phase dépend elle-même de la fréquence de l’onde, ce qui rend la relation entre la longueur d’onde et la fréquence non linéaire.
Dans le cas du rayonnement électromagnétique – tel que la lumière – en espace libre, la vitesse de phase est la vitesse de la lumière, soit environ 3×108 m/s. Ainsi, la longueur d’onde d’une onde électromagnétique (radio) de 100 MHz est d’environ : 3×108 m/s divisé par 108 Hz = 3 mètres. La longueur d’onde de la lumière visible va du rouge profond, environ 700 nm, au violet, environ 400 nm (pour d’autres exemples, voir spectre électromagnétique).
Pour les ondes sonores dans l’air, la vitesse du son est de 343 m/s (à température ambiante et à la pression atmosphérique). Les longueurs d’onde des fréquences sonores audibles par l’oreille humaine (20 Hz-20 kHz) sont donc comprises entre environ 17 m et 17 mm, respectivement. Les chauves-souris utilisent des fréquences un peu plus élevées pour pouvoir distinguer des cibles plus petites que 17 mm. Les longueurs d’onde du son audible sont beaucoup plus longues que celles de la lumière visible.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Par exemple, pour une onde électromagnétique, si la boîte a des parois métalliques idéales, la condition de nœuds aux parois résulte du fait que les parois métalliques ne peuvent pas supporter un champ électrique tangentiel, ce qui oblige l’onde à avoir une amplitude nulle à la paroi.
L’onde stationnaire peut être considérée comme la somme de deux ondes sinusoïdales mobiles de vitesses opposées. Par conséquent, la longueur d’onde, la période et la vitesse de l’onde sont liées comme pour une onde en déplacement. Par exemple, la vitesse de la lumière peut être déterminée à partir de l’observation d’ondes stationnaires dans une boîte métallique contenant un vide idéal.
Représentation mathématiqueModification
Les ondes sinusoïdales progressives sont souvent représentées mathématiquement en fonction de leur vitesse v (dans la direction x), de leur fréquence f et de leur longueur d’onde λ comme:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ). {\displaystyle y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}

où y est la valeur de l’onde à toute position x et au temps t, et A est l’amplitude de l’onde. Elles sont aussi couramment exprimées en termes de nombre d’onde k (2π fois l’inverse de la longueur d’onde) et de fréquence angulaire ω (2π fois la fréquence) comme:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ). {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}

dans lequel la longueur d’onde et le nombre d’onde sont liés à la vitesse et à la fréquence comme :
k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},

ou
λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}.}

Dans la deuxième forme donnée ci-dessus, la phase (kx – ωt) est souvent généralisée en (k-r – ωt), en remplaçant le nombre d’onde k par un vecteur d’onde qui précise la direction et le nombre d’onde d’une onde plane dans l’espace 3, paramétrée par le vecteur position r. Dans ce cas, le nombre d’onde k, la magnitude de k, est toujours dans la même relation avec la longueur d’onde comme montré ci-dessus, avec v étant interprété comme la vitesse scalaire dans la direction du vecteur d’onde. La première forme, utilisant la longueur d’onde réciproque dans la phase, ne se généralise pas aussi facilement à une onde dans une direction arbitraire.
Les généralisations aux sinusoïdes d’autres phases, et aux exponentielles complexes, sont également courantes ; voir onde plane. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. En particulier, la vitesse de la lumière dans un milieu est inférieure à celle du vide, ce qui signifie que la même fréquence correspondra à une longueur d’onde plus courte dans le milieu que dans le vide, comme le montre la figure de droite.
Ce changement de vitesse à l’entrée dans un milieu provoque la réfraction, ou un changement de direction des ondes qui rencontrent l’interface entre les milieux sous un angle. Pour les ondes électromagnétiques, ce changement d’angle de propagation est régi par la loi de Snell.
La vitesse des ondes dans un milieu peut non seulement différer de celle dans un autre, mais la vitesse varie généralement avec la longueur d’onde. Par conséquent, le changement de direction à l’entrée dans un milieu différent change avec la longueur d’onde de l’onde.
Pour les ondes électromagnétiques, la vitesse dans un milieu est régie par son indice de réfraction selon
v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},}

où c est la vitesse de la lumière dans le vide et n(λ0) est l’indice de réfraction du milieu à la longueur d’onde λ0, ce dernier étant mesuré dans le vide plutôt que dans le milieu. La longueur d’onde correspondante dans le milieu est
λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}

Lorsque des longueurs d’onde de rayonnement électromagnétique sont citées, la longueur d’onde dans le vide est généralement visée, sauf si la longueur d’onde est spécifiquement identifiée comme étant la longueur d’onde dans un autre milieu. En acoustique, où un milieu est essentiel pour que les ondes existent, la valeur de la longueur d’onde est donnée pour un milieu spécifié.
La variation de la vitesse de la lumière en fonction de la longueur d’onde est connue sous le nom de dispersion, et est également responsable du phénomène familier dans lequel la lumière est séparée en couleurs composantes par un prisme. La séparation se produit lorsque l’indice de réfraction à l’intérieur du prisme varie avec la longueur d’onde, de sorte que les différentes longueurs d’onde se propagent à des vitesses différentes à l’intérieur du prisme, ce qui les amène à se réfracter à des angles différents. La relation mathématique qui décrit comment la vitesse de la lumière à l’intérieur d’un milieu varie avec la longueur d’onde est connue sous le nom de relation de dispersion.
Moyens non uniformes

La longueur d’onde peut être un concept utile même si la vague n’est pas périodique dans l’espace. Par exemple, dans une vague océanique approchant du rivage, illustrée sur la figure, la vague entrante ondule avec une longueur d’onde locale variable qui dépend en partie de la profondeur du fond marin par rapport à la hauteur de la vague. L’analyse de la vague peut être basée sur la comparaison de la longueur d’onde locale avec la profondeur locale de l’eau.

Les ondes qui sont sinusoïdales dans le temps mais qui se propagent dans un milieu dont les propriétés varient avec la position (un milieu inhomogène) peuvent se propager à une vitesse qui varie avec la position et, par conséquent, ne pas être sinusoïdales dans l’espace. La figure de droite montre un exemple. Lorsque l’onde ralentit, la longueur d’onde se raccourcit et l’amplitude augmente ; après un lieu de réponse maximale, la courte longueur d’onde est associée à une forte perte et l’onde s’éteint.
L’analyse des équations différentielles de tels systèmes se fait souvent de manière approximative, en utilisant la méthode WKB (également connue sous le nom de méthode de Liouville-Green). Cette méthode intègre la phase à travers l’espace en utilisant un nombre d’onde local, qui peut être interprété comme indiquant une « longueur d’onde locale » de la solution en fonction du temps et de l’espace.Cette méthode traite localement le système comme s’il était uniforme avec les propriétés locales ; en particulier, la vitesse d’onde locale associée à une fréquence est la seule chose nécessaire pour estimer le nombre d’onde ou la longueur d’onde locale correspondante. En outre, la méthode calcule une amplitude qui change lentement pour satisfaire d’autres contraintes des équations ou du système physique, comme pour la conservation de l’énergie dans l’onde.
CristauxEdit
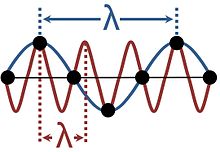
Les ondes dans les solides cristallins ne sont pas continues, car elles sont composées de vibrations de particules discrètes disposées dans un réseau régulier. Cela produit un aliasing car la même vibration peut être considérée comme ayant une variété de longueurs d’onde différentes, comme le montre la figure. Les descriptions utilisant plus d’une de ces longueurs d’onde sont redondantes ; il est conventionnel de choisir la plus grande longueur d’onde qui correspond au phénomène. La gamme de longueurs d’onde suffisante pour fournir une description de toutes les ondes possibles dans un milieu cristallin correspond aux vecteurs d’onde confinés dans la zone de Brillouin.
Cette indétermination de la longueur d’onde dans les solides est importante dans l’analyse des phénomènes ondulatoires tels que les bandes d’énergie et les vibrations du réseau. Elle est mathématiquement équivalente au crénelage d’un signal échantillonné à intervalles discrets.
La longueur d’onde des solides est indéterminée.