Golflengte
In lineaire media kan elk golfpatroon worden beschreven in termen van de onafhankelijke voortplanting van sinusoïdale componenten. De golflengte λ van een sinusoïdale golfvorm met constante snelheid v wordt gegeven door
λ = v f , {\displaystyle \lambda ={\frac {v}{f}},\,,}

waarin v de fasesnelheid (grootte van de fasesnelheid) van de golf wordt genoemd en f de frequentie van de golf is. In een dispersief medium hangt de fasesnelheid zelf af van de frequentie van de golf, waardoor het verband tussen golflengte en frequentie niet-lineair is.
In het geval van elektromagnetische straling, zoals licht in de vrije ruimte, is de fasesnelheid de lichtsnelheid, ongeveer 3×108 m/s. Dus de golflengte van een 100 MHz elektromagnetische (radio) golf is ongeveer: 3×108 m/s gedeeld door 108 Hz = 3 meter. De golflengte van zichtbaar licht varieert van dieprood, ruwweg 700 nm, tot violet, ruwweg 400 nm (voor andere voorbeelden, zie elektromagnetisch spectrum).
Voor geluidsgolven in lucht is de geluidssnelheid 343 m/s (bij kamertemperatuur en atmosferische druk). De golflengten van de voor het menselijk oor hoorbare geluidsfrequenties (20 Hz-20 kHz) liggen dus respectievelijk tussen ongeveer 17 m en 17 mm. Iets hogere frequenties worden door vleermuizen gebruikt om doelen kleiner dan 17 mm te kunnen waarnemen. Golflengten in hoorbaar geluid zijn veel langer dan die in zichtbaar licht.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Bijvoorbeeld, voor een elektromagnetische golf, indien de doos ideale metalen wanden heeft, resulteert de voorwaarde voor knopen aan de wanden omdat de metalen wanden geen tangentieel elektrisch veld kunnen ondersteunen, waardoor de golf gedwongen wordt bij de wand een nulamplitude te hebben.
De stationaire golf kan worden gezien als de som van twee bewegende sinusoïdale golven met tegengesteld gerichte snelheden. Bijgevolg zijn golflengte, periode en golfsnelheid aan elkaar gerelateerd, net als bij een bewegende golf. Zo kan bijvoorbeeld de lichtsnelheid worden bepaald uit de waarneming van staande golven in een metalen doos met een ideaal vacuüm.
Wiskundige weergaveEdit
Reizende sinusgolven worden vaak wiskundig voorgesteld in termen van hun snelheid v (in de x-richting), frequentie f en golflengte λ als:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) = A cos ( 2 π λ ( x – v t ) ) {\displaystyle y(x,t)=Acos \left(2ambda }}-ft-rechts)=Acos \left(2ambda }(x-vt)\rechts)}

waarbij y de waarde van de golf is op elke positie x en tijd t, en A de amplitude van de golf is. Zij worden ook gewoonlijk uitgedrukt in termen van het golfgetal k (2π maal het reciproke van de golflengte) en de hoekfrequentie ω (2π maal de frequentie) als:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) {displaystyle y(x,t)=Acos \links(kx-omega t)=Acos \links(k(x-vt)}

waarin golflengte en golfgetal zijn gerelateerd aan snelheid en frequentie als:
k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},

of
λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.}

In de tweede vorm hierboven wordt de fase (kx – ωt) vaak veralgemeend tot (k-r – ωt), door het golfgetal k te vervangen door een golfvector die de richting en het golfgetal aangeeft van een vlakke golf in de 3-ruimte, geparametriseerd door de positievector r. In dat geval staat het golfgetal k, de grootte van k, nog steeds in hetzelfde verband met de golflengte als hierboven getoond, waarbij v wordt geïnterpreteerd als scalaire snelheid in de richting van de golfvector. De eerste vorm, waarbij de reciproke golflengte in de fase wordt gebruikt, generaliseert niet zo gemakkelijk naar een golf in een willekeurige richting.
Generalisaties naar sinusoïden van andere fasen, en naar complexe exponentialen, zijn ook gebruikelijk; zie vlakke golf. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. In het bijzonder is de lichtsnelheid in een medium lager dan in vacuüm, hetgeen betekent dat dezelfde frequentie in het medium overeenkomt met een kortere golflengte dan in vacuüm, zoals te zien is in de figuur rechts.
Deze snelheidsverandering bij het binnentreden van een medium veroorzaakt breking, of een verandering in de richting van golven die het grensvlak tussen media onder een hoek tegenkomen. Voor elektromagnetische golven wordt deze verandering in de voortplantingshoek beheerst door de wet van Snell.
De golfsnelheid in het ene medium kan niet alleen verschillen van die in een ander medium, maar de snelheid varieert gewoonlijk met de golflengte. Dientengevolge verandert de verandering van richting bij het binnengaan van een ander medium met de golflengte van de golf.
Voor elektromagnetische golven wordt de snelheid in een medium bepaald door zijn brekingsindex volgens
v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},}

waarbij c de lichtsnelheid in vacuüm is en n(λ0) de brekingsindex van het medium bij golflengte λ0, waarbij deze laatste wordt gemeten in vacuüm en niet in het medium. De overeenkomstige golflengte in het medium is
λ = λ 0 n ( λ 0 ) . {\displaystyle λlambda ={\frac {\lambda _{0}}{n(λlambda _{0})}}.}

Wanneer golflengten van elektromagnetische straling worden vermeld, wordt meestal de golflengte in vacuüm bedoeld, tenzij de golflengte specifiek wordt aangeduid als de golflengte in een ander medium. In de akoestiek, waar een medium essentieel is voor het bestaan van de golven, wordt de golflengtewaarde gegeven voor een gespecificeerd medium.
De variatie in de snelheid van licht met de golflengte staat bekend als dispersie, en is ook verantwoordelijk voor het bekende verschijnsel waarbij licht door een prisma wordt gescheiden in samenstellende kleuren. De scheiding ontstaat wanneer de brekingsindex binnen het prisma varieert met de golflengte, zodat verschillende golflengten zich met verschillende snelheden binnen het prisma voortplanten, waardoor ze onder verschillende hoeken breken. De wiskundige relatie die beschrijft hoe de snelheid van licht in een medium varieert met de golflengte staat bekend als een dispersie relatie.
Niet-uniforme media

Golflengte kan een nuttig begrip zijn, zelfs als de golf niet periodiek in de ruimte is. Bijvoorbeeld, in een oceaangolf die de kust nadert, zoals in de figuur is te zien, golft de binnenkomende golf met een variërende plaatselijke golflengte die gedeeltelijk afhangt van de diepte van de zeebodem in vergelijking met de golfhoogte. De analyse van de golf kan worden gebaseerd op een vergelijking van de plaatselijke golflengte met de plaatselijke waterdiepte.

Golven die sinusoïdaal in de tijd zijn, maar zich voortplanten door een medium waarvan de eigenschappen variëren met de positie (een inhomogeen medium), kunnen zich voortplanten met een snelheid die varieert met de positie, en als gevolg daarvan mogelijk niet sinusoïdaal in de ruimte zijn. De figuur rechts toont een voorbeeld. Naarmate de golf langzamer gaat, wordt de golflengte korter en neemt de amplitude toe; na een plaats van maximale respons gaat de korte golflengte gepaard met een groot verlies en sterft de golf uit.
De analyse van differentiaalvergelijkingen van dergelijke systemen wordt vaak bij benadering gedaan, met behulp van de WKB-methode (ook bekend als de Liouville-Green methode). De methode integreert de fase door de ruimte met behulp van een lokaal golfgetal, dat kan worden geïnterpreteerd als een aanduiding van een “lokale golflengte” van de oplossing als functie van tijd en ruimte.Deze methode behandelt het systeem lokaal alsof het uniform is met de lokale eigenschappen; in het bijzonder is de lokale golfsnelheid die bij een frequentie hoort het enige dat nodig is om het bijbehorende lokale golfgetal of de golflengte te schatten. Bovendien berekent de methode een langzaam veranderende amplitude om te voldoen aan andere beperkingen van de vergelijkingen of van het fysische systeem, zoals voor het behoud van energie in de golf.
KristallenEdit
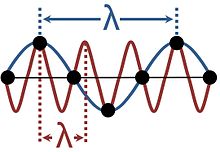
Golven in kristallijne vaste stoffen zijn niet continu, omdat zij zijn opgebouwd uit trillingen van discrete deeltjes die in een regelmatig rooster zijn gerangschikt. Dit leidt tot aliasing, omdat dezelfde trilling een aantal verschillende golflengten kan hebben, zoals in de figuur is te zien. Beschrijvingen waarbij meer dan één van deze golflengten wordt gebruikt, zijn overbodig; het is gebruikelijk de langste golflengte te kiezen die bij het verschijnsel past. Het bereik van golflengten dat voldoende is om een beschrijving te geven van alle mogelijke golven in een kristallijn medium komt overeen met de golfvectoren die beperkt zijn tot de Brillouin-zone.
Deze onbepaaldheid in golflengte in vaste stoffen is belangrijk bij de analyse van golfverschijnselen zoals energiebanden en tralietrillingen. Het is wiskundig equivalent aan de aliasing van een signaal dat met discrete intervallen wordt bemonsterd.