A növekvő járadék jövőbeli értéke
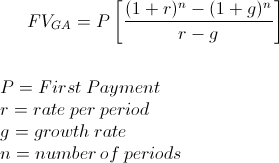
A növekvő járadék jövőbeli értékének képletét arra használják, hogy kiszámítsák egy sor, arányosan növekvő pénzáramlás vagy kifizetés jövőbeli összegét. A növekvő járadékot néha növekvő járadéknak is nevezik.
Példa a növekvő járadék jövőbeli értékére
A növekvő járadék jövőbeli értékének képletére egy példa egy olyan személy, aki kéthetente kap fizetést, és úgy dönt, hogy évente egy extra fizetését megtakarítja. Az első évben az egyik nettó fizetése 2000 dollárt tesz ki, és arra számít, hogy minden évben 5%-os emelést kap a nettó fizetésére. Ebben a példában a nettó fizetésének 5%-át fogjuk használni, és nem vesszük figyelembe az adókat és egyéb kiigazításokat, hogy minden más dolgot állandónak tartsunk. Egy évi 3%-os hozamú számlán szeretné kiszámítani a megtakarítási egyenlegét 5 év után.
A növekedési ráta ebben a példában az évi 5%-os növekedés lenne, a kezdeti pénzáramlás vagy kifizetés 2000 dollár, az időszakok száma 5 év, az időszakonkénti ráta pedig 3%. Ha ezeket a változókat használjuk a növekvő járadék jövőbeli értékének képletében, akkor
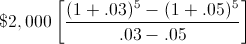
Az egyenlet megoldása után az 5. pénzáramlás után az összeg 11.700,75 $ lenne.
Hogyan származtatható a növekvő járadék jövőbeli értéke?
A növekvő járadék jövőbeli értékét úgy találhatjuk meg, ha először a következő növekvő járadék jelenértékének képletét nézzük
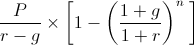
A jelenértéket a jelenérték és (1+r)n szorzatával alakíthatjuk át jövőbeli értékké. By multiplying the 2nd portion of the PV of growing annuity formula above by (1+r)n, the formula would show as
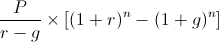
From here, the formula above is the same as the formula shown at the top of the page after factoring out the initial payment, P.
Return to Top
- Formulas related to FV of Growing Annuity
- PV of Growing Annuity
- FV of Annuity
- FV of Annuity Due
- Growing Annuity Payment (FV)