Az elméleti valószínűség kontra kísérleti valószínűség
Az elméleti valószínűség és a kísérleti valószínűség kifejezéseket már hallotta, de mit jelentenek?
Egyáltalán kapcsolatban állnak egymással? Ezt fogjuk felfedezni ebben a leckében.
Ha elvégezted a független és a függő valószínűségről szóló leckéket, akkor már számos problémára megtaláltad az elméleti valószínűséget.
Az elméleti valószínűség
Az elméleti valószínűség az a valószínűség, amelyet matematikai képletek segítségével számítunk ki. Ez a matematikai elméleten alapuló valószínűség.
Kísérleti valószínűség
A kísérleti valószínűséget akkor számítják ki, amikor a tényleges helyzetet vagy problémát kísérletként hajtják végre. Ebben az esetben elvégeznéd a kísérletet, és a tényleges eredményeket használnád a valószínűség meghatározásához.
A kísérlet pontos elvégzéséhez a következőket kell tenned:
- Meghatározni, hogy mi számít “kísérletnek”.
- Minimum 25 kísérletet kell elvégezned
- Elkészítened egy szervezőt (táblázatot vagy diagramot) az adatok rögzítéséhez.
Nézzünk egy példát, ahol először kiszámítjuk az elméleti valószínűséget, majd elvégezzük a kísérletet a kísérleti valószínűség meghatározásához.
Érdekes lesz összehasonlítani az elméleti valószínűséget és a kísérleti valószínűséget. Ön szerint a két számítás közel lesz egymáshoz?
1. példa – Elméleti kontra kísérleti
Ez a feladat a független események lecke 1. példájából származik. Kiszámítottuk, hogy az elméleti valószínűség 1/12 vagy 8,3%. Nézzük meg:
elméleti valószínűség

Ha már tudjuk, hogy az elméleti valószínűség 8,3% az esélye annak, hogy fejet dobunk és 6-ost dobunk, nézzük meg, mi történik, ha ténylegesen elvégezzük a kísérletet.
Kísérleti valószínűség
Kijelölünk egy kísérletet: Egy kísérlet abból áll, hogy egyszer feldobunk egy érmét és egyszer dobunk egy kockát.
Végezzünk 25 kísérletet, és rögzítsük az adatokat az alábbi táblázatban.
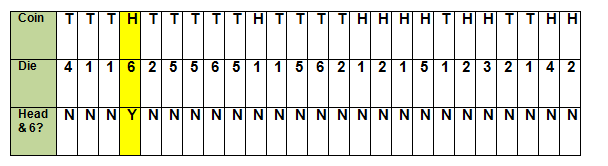
Minden kísérletnél egyszer feldobtam az érmét és egyszer dobtam a kockával. Az “Érme” feliratú sorban feljegyeztem egy H-t a fej és egy T-t az írás esetén.
A “Kocka” feliratú sorban feljegyeztem a kockán lévő számot.
Az utolsó sorban meghatároztam, hogy a kísérlet befejezte-e a fej feldobásának és a hatos gurításának eseményét.
A kísérletben csak 1 olyan kísérlet volt (25-ből), ahol fejet dobtak az érmére és 6-ost dobtak a kockára.
Ez azt jelenti, hogy a kísérleti valószínűség 1/25 vagy 4%.
Tipp
Figyeljünk arra, hogy mindenki kísérlete eltérő lesz; így a kísérleti valószínűség is eltérő lehet.
Azt is tudd, hogy minél több kísérletet végzel a kísérletedben, annál közelebb lesznek a számításaid a kísérleti és az elméleti valószínűségekhez.
Következtetések
Az elméleti valószínűség 8,3%, a kísérleti valószínűség pedig 4%. Bár a kísérleti valószínűség valamivel alacsonyabb, ez nem jelentős különbség.
A legtöbb kísérletben az elméleti valószínűség és a kísérleti valószínűség nem lesz egyenlő, azonban viszonylag közel kell lenniük egymáshoz.
If the calculations are not close, then there’s a possibility that the experiment was conducted improperly or more trials need to be completed.
I hope this helps to give you a sense of how to set up an experiment in order to compare theoretical versus experimental probabilities.
- Home
- Probability
- Theoretical/Experimental Probability
>
>

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.