Az interpoláció típusai – előnyök és hátrányok
Interpolációs módszerek
Az interpoláció az ismert értékekkel rendelkező pontok vagy mintapontok felhasználása más ismeretlen pontok értékeinek becslésére. Bármilyen földrajzi pontadat ismeretlen értékeinek előrejelzésére használható, például magasság, csapadék, kémiai koncentrációk, zajszintek és így tovább.
A rendelkezésre álló interpolációs módszerek az alábbiakban vannak felsorolva.
Inverz távolsággal súlyozott (IDW)
Az inverz távolsággal súlyozott interpolátor feltételezi, hogy minden bemeneti pontnak van egy helyi hatása, amely a távolsággal csökken. A feldolgozó cellához közelebbi pontokat nagyobb súllyal súlyozza, mint a távolabbiakat. Az egyes helyek kimeneti értékének meghatározásához meghatározott számú pont vagy egy meghatározott sugarú körben lévő összes pont használható. E módszer használata feltételezi, hogy a leképezendő változó befolyása a mintavételi helytől való távolsággal csökken.
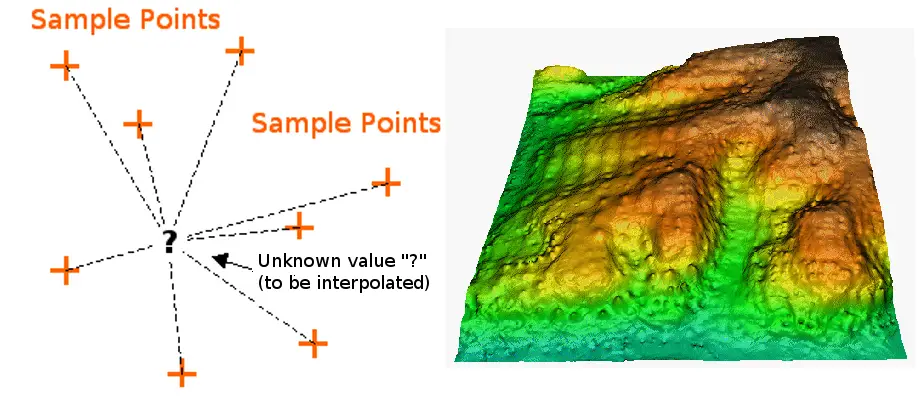
IDW Interpolation; Courtesy: QGIS
Az Inverse Distance Weighting (IDW) algoritmus gyakorlatilag egy mozgóátlag interpolátor, amelyet általában erősen változó adatokra alkalmaznak. Bizonyos adattípusok esetében lehetőség van arra, hogy visszatérjünk a gyűjtési helyre, és olyan új értéket rögzítsünk, amely statisztikailag eltér az eredeti leolvasástól, de a terület általános trendjén belül van.
A mozgóátlag technikával becsült interpolált felület kisebb a helyi maximális értéknél és nagyobb a helyi minimális értéknél.

IDW interpolált felület; Courtesy:ESRI
AzIDW interpoláció kifejezetten azt a feltételezést valósítja meg, hogy az egymáshoz közeli dolgok jobban hasonlítanak egymásra, mint az egymástól távolabbiak. Bármely nem mért hely értékének előrejelzéséhez az IDW az előrejelzési helyet körülvevő mért értékeket használja. Az előrejelzési helyhez legközelebbi mért értékek nagyobb hatással lesznek az előrejelzett értékre, mint a távolabbiak. Az IDW tehát feltételezi, hogy minden egyes mért pontnak helyi hatása van, amely a távolsággal csökken. Az IDW függvényt akkor kell használni, ha a pontok halmaza elég sűrű ahhoz, hogy az elemzéshez szükséges helyi felszínváltozások mértékét meg lehessen ragadni. Az IDW a mintapontok lineárisan súlyozott kombinált halmazának felhasználásával határozza meg a cellaértékeket. Az előrejelzés helyéhez közelebbi pontokat nagyobb súllyal súlyozza, mint a távolabbiakat, innen az inverz távolsággal súlyozott elnevezés.
Az IDW-technika minden egyes rácscsomóponthoz úgy számít ki egy értéket, hogy megvizsgálja a környező adatpontokat, amelyek egy felhasználó által meghatározott keresési sugaron belül helyezkednek el. Az adatpontok egy része vagy mindegyike felhasználható az interpolációs folyamat során. A csomópont értéke az összes pont súlyozott összegének átlagolásával kerül kiszámításra. A csomóponttól egyre távolabb eső adatpontok sokkal kevésbé befolyásolják a kiszámított értéket, mint a csomóponthoz közelebb esőek.
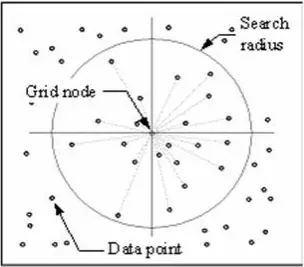
Minden rácscsomópont körül létrejön egy sugár, amelyből az adatpontok kiválasztásra kerülnek a számításhoz. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Egy másik súlyozott átlagolási módszer, a természetes szomszéd interpolációban használt alapegyenlet megegyezik az IDW interpolációban használtal. Ez a módszer hatékonyan képes kezelni a nagy bemeneti pontadathalmazokat. A természetes szomszéd módszer használatakor a helyi koordináták határozzák meg, hogy az egyes szóráspontok mekkora befolyást gyakorolnak a kimeneti cellákra.
A természetes szomszéd módszer egy geometriai becslési technika, amely az adathalmaz minden egyes pontja körül létrehozott természetes szomszédsági régiókat használ.
Az IDW módszerhez hasonlóan ez az interpolációs módszer is súlyozott átlagú interpolációs módszer. Ahelyett azonban, hogy az interpolált pont értékét a távolságukkal súlyozott összes bemeneti pont felhasználásával találná meg, a Natural Neighbors interpoláció létrehozza a bemeneti pontok Delauney-triangulációját, és kiválasztja a legközelebbi csomópontokat, amelyek konvex burkot alkotnak az interpolációs pont körül, majd értéküket arányosan súlyozza. Ez a módszer akkor a legmegfelelőbb, ha a mintaadatok pontjai egyenetlen sűrűséggel oszlanak el. Ez egy jó általános célú interpolációs technika, és előnye, hogy nem kell megadni olyan paramétereket, mint a sugár, a szomszédok száma vagy a súlyok.

Natural IDW: Courtesy: ESRI
Ez a technika a pontfájl helyi minimum- és maximumértékeinek tiszteletben tartására szolgál, és beállítható a helyi magas értékek túllépésének és a helyi alacsony értékek alácsúszásának korlátozására. A módszer ezáltal lehetővé teszi pontos felszínmodellek létrehozását olyan adathalmazokból, amelyek nagyon ritkán vagy nagyon lineárisan térbeli eloszlásúak.
Előnyök
- Egy nagyszámú mintapont hatékony kezelése.
Spline
A Spline olyan matematikai függvény segítségével becsüli az értékeket, amely minimalizálja a teljes felületi görbületet, így olyan sima felületet kap, amely pontosan áthalad a bemeneti pontokon.

Spline: Courtesy: ESRI
Koncepcionálisan analóg egy gumilap meghajlításával, hogy ismert pontokon haladjon át, miközben minimalizálja a felület teljes görbületét. Egy matematikai függvényt illeszt a legközelebbi bemeneti pontok meghatározott számához, miközben áthalad a mintapontokon. Ez a módszer a legjobb az enyhén változó felületek, például a tengerszint feletti magasság, a talajvízszint magassága vagy a szennyezés koncentrációja esetén.
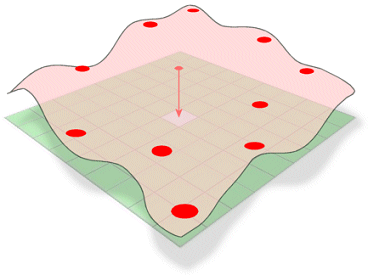
A Spline interpolációs módszer úgy becsül ismeretlen értékeket, hogy egy felületet ismert értékeken keresztül hajlít meg.
Két Spline-módszer létezik: a regularizált és a feszített.
A regularizált módszer sima, fokozatosan változó felületet hoz létre olyan értékekkel, amelyek a mintaadatok tartományán kívül eshetnek. A minimalizálási számításokba beépíti az első deriváltat (meredekség), a második deriváltat (a meredekség változásának mértéke) és a harmadik deriváltat (a második derivált változásának mértéke).
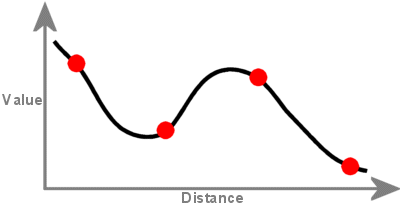
A Spline-interpolációval létrehozott felület minden egyes mintaponton áthalad, és meghaladhatja a mintapontkészlet értéktartományát.
Bár a Tension spline csak az első és második deriváltat használja, több pontot von be a Spline-számításokba, ami általában simább felületeket hoz létre, de növeli a számítási időt.
Ez a módszer egy felületet húz át a felvett pontokon, ami megnyújtott hatást eredményez. A Spline görbe vonalakat használ (görbe vonalak módszer) a cellák értékeinek kiszámításához.
Súly kiválasztása a Spline interpolációkhoz
Regularizált spline: Minél nagyobb a súly, annál simább a felület. A 0 és 5 közötti súlyok megfelelőek. Tipikus értékek a 0, .001, .01, .1 és .5.
Feszített spline: Minél nagyobb a súly, annál durvább a felület, és az értékek jobban megfelelnek a mintaadatok tartományának. A súlyértékeknek nullánál nagyobbnak vagy egyenlőnek kell lenniük. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Kriging eljárás, amely egy becsült felületet hoz létre a z-értékekkel rendelkező pontok szórt halmazából. A Kriging feltételezi, hogy a mintapontok közötti távolság vagy irány egy olyan térbeli korrelációt tükröz, amely felhasználható a felszín változásának magyarázatára. A Kriging eszköz egy matematikai függvényt illeszt egy megadott számú pontra vagy egy megadott sugarú körben lévő összes pontra, hogy meghatározza az egyes helyekre vonatkozó kimeneti értéket. A Kriging egy többlépcsős folyamat; magában foglalja az adatok feltáró statisztikai elemzését, a variogram modellezését, a felület létrehozását és (opcionálisan) a varianciafelület feltárását. A Kriging akkor a legmegfelelőbb, ha tudjuk, hogy az adatokban térbeli korrelációval összefüggő távolság vagy iránybeli torzítás van. Gyakran használják a talajtanban és a geológiában.
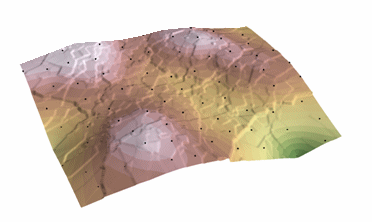
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
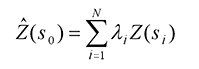
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. A kriging módszerrel azonban a súlyok nem csak a mért pontok és az előrejelzési hely közötti távolságon alapulnak, hanem a mért pontok általános térbeli elrendezésén is. A térbeli elrendezésnek a súlyokban való felhasználásához a térbeli autokorrelációt számszerűsíteni kell. Így a hagyományos krigingben a λi súly a mért pontokra illesztett modelltől, a predikciós helytől való távolságtól és a mért értékek közötti térbeli kapcsolatoktól függ a predikciós hely körül. A következő szakaszok azt tárgyalják, hogy az általános kriging-képlet hogyan használható az előrejelzési felület térképének és az előrejelzések pontosságának térképének létrehozására.
A Kriging típusai
Ordináris Kriging
Az ordináris kriging feltételezi a modellt
Z(s) = µ + ε(s),
ahol µ egy ismeretlen állandó. A közönséges kriginggel kapcsolatos egyik fő kérdés, hogy ésszerű-e az állandó átlag feltételezése. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indikátoros kriging
Az indikátoros kriging feltételezi a modellt
I(s) = µ + ε(s),
ahol µ egy ismeretlen konstans és I(s) egy bináris változó. A bináris adatok létrehozása történhet folytonos adatok esetén küszöbérték alkalmazásával, vagy lehet, hogy a megfigyelt adatok 0 vagy 1 értékűek. Például rendelkezhetünk olyan mintával, amely arra vonatkozó információkból áll, hogy egy pont erdei vagy nem erdei élőhely-e, ahol a bináris változó az osztályhoz tartozást jelzi. A bináris változók használatával az indikátoros kriging ugyanúgy jár el, mint a közönséges kriging.
Az indikátoros kriging használhat szemivariogramokat vagy kovarianciákat.
Valószínűségi krigelés
A valószínűségi krigelés feltételezi a modellt
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
amelyben µ1 és µ2 ismeretlen konstansok és I(s) egy küszöbmutató használatával létrehozott bináris változó, I(Z(s) > ct). Vegyük észre, hogy most kétféle véletlen hiba van, ε1(s) és ε2(s), tehát mindegyiknél van autokorreláció, és van köztük keresztkorreláció. A valószínűségi kriging ugyanarra törekszik, mint az indikátoros kriging, de a cokriginget használja, hogy jobb munkát végezzen.
A valószínűségi kriging használhat semivariogramokat vagy kovarianciákat, kereszt-kovarianciákat és transzformációkat, de nem tudja figyelembe venni a mérési hibát.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-slot=”9271753327″>
Diszjunktív kriging
A diszjunktív kriging feltételezi a modellt
f(Z(s)) = µ1 + ε(s),
amelyben µ1 egy ismeretlen konstans és f(Z(s)) a Z(s) egy tetszőleges függvénye. Vegyük észre, hogy f(Z(s)) = I(Z(s) > ct) írható, tehát az indikátoros kriging a diszjunktív kriging speciális esete. A Geostatistical Analystban diszjunktív krigeléssel vagy magát az értéket, vagy egy indikátort lehet megjósolni.
A diszjunktív kriging általában többre törekszik, mint a közönséges kriging. Míg az előnyök nagyobbak lehetnek, a költségek is nagyobbak. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** A Kriging matematikai megközelítésének mélyebb megértéséhez kattintson a Kriging egy interpolációs módszerre.
PointInterp
Az IDW-hez hasonló módszer, a PointInterp függvény nagyobb ellenőrzést tesz lehetővé a mintavételi szomszédság felett. Egy adott minta hatása az interpolált rácscella értékére attól függ, hogy a mintapont a cella szomszédságában van-e, és milyen messze található az interpolálandó cellától. A szomszédságon kívüli pontoknak nincs hatása.

PointInterp; Courtesy: ESRI
A szomszédságon belüli pontok súlyozott értéke inverz távolsággal súlyozott interpoláció vagy inverz exponenciális távolság interpoláció segítségével kerül kiszámításra. Ez a módszer pontjellemzők segítségével interpolálja a rasztert, de különböző típusú szomszédságokat tesz lehetővé. A szomszédságok formája lehet például kör, téglalap, szabálytalan sokszög, gyűrű vagy ék.
Trend
A trend egy olyan statisztikai módszer, amely a legkisebb négyzetes regressziós illesztés segítségével megtalálja azt a felületet, amely illeszkedik a mintapontokhoz. Egyetlen polinomiális egyenletet illeszt a teljes felületre. Ez olyan felületet eredményez, amely minimalizálja a felület szórását a bemeneti értékekhez képest. A felületet úgy építi fel, hogy minden bemeneti pont esetében a tényleges értékek és a becsült értékek közötti különbségek összege (azaz a variancia) a lehető legkisebb legyen.

Trend; Courtsey:ESRI
Ez egy nem pontos interpolátor, és a kapott felület ritkán halad át a bemeneti pontokon. Ez a módszer azonban felismeri a mintaadatokban a trendeket, és hasonlít a természeti jelenségekhez, amelyek jellemzően simán változnak.
Előny
- A trendfelületek jól alkalmasak az adatok durva léptékű mintázatainak azonosítására; az interpolált felület ritkán halad át a mintapontokon.
Topo to Raster
A Topo to Raster módszer a raszterhez tartozó magassági értékek interpolálásával olyan megkötéseket ír elő, amelyek biztosítják a hidrológiailag helyes digitális magassági modellt, amely összefüggő vízgyűjtő szerkezetet tartalmaz, és helyesen ábrázolja a gerinceket és patakokat a bemeneti magassági adatokból. A módszer iteratív véges differencia interpolációs technikát alkalmaz, amely optimalizálja a helyi interpoláció számítási hatékonyságát anélkül, hogy elveszítené a globális interpoláció felszíni folytonosságát. Kifejezetten úgy tervezték, hogy intelligensen működjön a kontúr bemeneti adatokkal.
Az alábbiakban egy példa a Topo to Raster interpolációval magassági pontokból, kontúrvonalakból, patakvonalakból és tópoligonokból interpolált felületre.
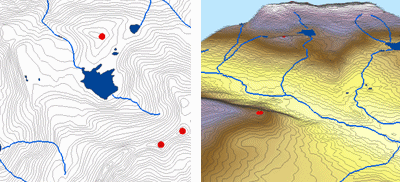
Topo to raster; Courtesy: ESRI
ATopo to Raster egy speciális eszköz, amellyel a terepkomponensek vektoros adataiból, például magassági pontokból, szintvonalakból, patakvonalakból, tópoligonokból, vízgyűjtő pontokból és vizsgálati terület határának poligonjaiból hidrológiailag helyes raszterfelületeket hozhatunk létre.
Sűrűség
A (az ArcGIS-ben elérhető) sűrűségi eszközök olyan felületet állítanak elő, amely azt mutatja meg, hogy egységnyi területre hány vagy hány darab jut valamilyen dologból. A sűrűség eszköz hasznos sűrűségfelületek létrehozására, hogy egy vadon élő állatállomány eloszlását ábrázolja egy megfigyelési halmazból, vagy egy terület urbanizáltsági fokát az utak sűrűsége alapján.

Density Raster; Courtest: ERSI
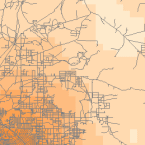
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method