dB: Mi az a decibel?

A hangnyomás, a hangszint és a dB. A hangot általában mikrofonokkal mérik, és ezek a hangnyomással, p-vel arányosan reagálnak. Nos, a hanghullámban lévő teljesítmény – minden más tényezőtől függetlenül – a nyomás négyzetével növekszik. (Hasonlóképpen, az elektromos teljesítmény egy ellenállásban a feszültség négyzetével nő.) Az x2 logaritmusa egyszerűen 2 log x, így ez egy 2-es tényezőt vezet be, amikor a nyomásarányokat decibelre konvertáljuk. A hangnyomásszint különbsége két p1 és p2 értékű hang között tehát:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (végig a log 10-es bázisra vonatkozik).

Mi történik, ha megfelezzük a hangteljesítményt? A 2 logaritmusa 0,3010, így az 1/2 logaritmusa jó közelítéssel -0,3. Ha tehát megfelezzük a teljesítményt, akkor a teljesítményt és a hangszintet 3 dB-lel csökkentjük. Ha újra megfelezzük (az eredeti teljesítmény 1/4-ére), akkor a hangszintet további 3 dB-lel csökkentjük. Ha tovább felezi a teljesítményt, akkor ezeket az arányokat kapja.

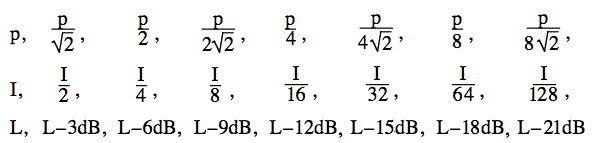
Mi történik, ha két azonos hangot adok hozzá? Megduplázom az intenzitást (3 dB-es növekedés)? Vagy megduplázom a nyomást (6 dB-es növekedés)? Ez a gyakran feltett kérdés kissé árnyalt, ezért itt a GYIK-ben tárgyaljuk.

Hangfájlok a decibel nagyságának bemutatására

Fentebb láttuk, hogy a teljesítmény megfelezése √2-vel csökkenti a hangnyomást és 3 dB-lel a hangszintet. Ezt tettük az alábbi első grafikonon és hangfájlban is.

Az első hangminta fehér zaj (a hallható frekvenciák széles tartományának keveréke, analóg a fehér fényhez, amely az összes látható frekvencia keveréke). A második minta ugyanez a zaj, √2-szeresére csökkentett feszültséggel. Most 1/√2 körülbelül 0,7, tehát a -3 dB megfelel a feszültség vagy a nyomás eredeti értékének 70%-ára való csökkentésének. A zöld vonal a feszültséget mutatja az idő függvényében. A piros vonal egy folyamatos exponenciális csökkenést mutat az idővel. Vegyük észre, hogy a feszültség minden második minta esetén 50%-kal csökken. Vegyük észre azt is, hogy a teljesítmény megduplázása nem okoz óriási különbséget a hangosságban. Ezt a későbbiekben még tárgyaljuk, de hasznos megjegyezni a hangvisszaadó berendezések kiválasztásakor. A hangfájlok és az animáció John Tann és George Hatsidimitris munkája.

Mekkora egy decibel? A következő sorozatban az egymást követő mintákat csak egy decibellel csökkentjük.

Egy decibel nagyságrendileg megegyezik a hangerősség épp észlelhető különbségével (JND). Ha meghallgatja ezeket a fájlokat, észre fogja venni, hogy az utolsó halkabb, mint az első, de az már kevésbé egyértelmű a fül számára, hogy bármelyik pár második tagja halkabb, mint az elődje. 10*log10(1,26) = 1, tehát a hangszint 1 dB-lel való növeléséhez a teljesítményt 26%-kal, vagy a feszültséget 12%-kal kell növelni.

És ha a különbség kevesebb, mint egy decibel? A hangszinteket ritkán adják meg tizedesjegyekkel. Ennek az az oka, hogy az 1 dB-nél kisebb különbségű hangszinteket nehéz megkülönböztetni, ahogy a következő példa is mutatja.(Ez teszi a dB-t egy kényelmes méretegységgé.)

0,3 dB lépések. Észreveheti, hogy az utolsó halkabb, mint az első, de az egymást követő párok között nehéz észrevenni a különbséget. 10*log10(1,07) = 0,3, tehát a hangszint 0,3 dB-rel való növeléséhez a teljesítményt 7%-kal, vagy a feszültséget 3,5%-kal kell növelni.

Standard referenciaszintek (“abszolút” hangszint)

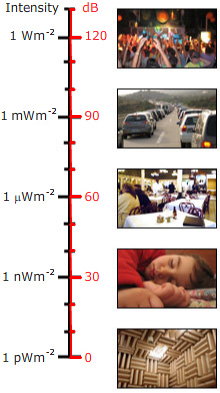Fentebb azt mondtuk, hogy a decibel egy arányszám. Ha tehát nem arányszámot, hanem egyetlen hang zajszintjének megadására használjuk, akkor egy referenciaszintet kell választani. A hangnyomásszint esetében a referenciaszintet (levegőre) általában úgy választják, hogy pref = 20 mikropaszkál (20 μPa), vagy 0,02 mPa. Ez nagyon alacsony: 2 tízmilliárdod része a légkörnek. Mindazonáltal ez körülbelül az emberi fül érzékenységének határát jelenti, annak érzékeny frekvenciatartományában. (Általában ez az érzékenység csak meglehetősen fiatal embereknél fordul elő, vagy olyanoknál, akik nem voltak kitéve hangos zenének vagy más hangos zajoknak. A fülbe épített hangszórókkal ellátott személyi zenei rendszerek nagyon magas hangszintet képesek a fülbe juttatni, és egyesek szerint ezek felelősek egyes országokban a fiatal felnőttek halláskárosodásának nagy részéért).

Ha tehát 86 dB hangnyomásszintről olvasunk, az azt jelenti, hogy

20 log (p2/pref) = 86 dB

ahol pref a referenciaszint hangnyomása, p2 pedig a szóban forgó hangé. Osszuk el mindkét oldalt 20-zal:

log (p2/pref) = 4,3

p2/pref = 104,3

4 a 10 ezer logaritmusa, 0,3 a 2 logaritmusa, tehát ennek a hangnak a hangnyomás 20 ezerszer nagyobb, mint a referenciaszinté (p2/pref = 20 000), vagy 400 milliószorosa a referenciaintenzitásnak. A 86 dB hangos hang, de nem veszélyes – feltéve, hogy az expozíció rövid ideig tart.

Mit jelent a 0 dB? Ez a szint akkor következik be, amikor a mért intenzitás megegyezik a referenciaszinttel, azaz ez a 0,02 mPa értéknek megfelelő hangszint. Ebben az esetben

hangszint = 20 log (pmért/pref) = 20 log 1 = 0 dB

Ne feledje, hogy a decibelek egy arányt mérnek. A 0 dB akkor áll elő, ha az 1 arány logaritmusát vesszük (log 1 = 0). Tehát a 0 dB nem azt jelenti, hogy nincs hang, hanem olyan hangszintet, ahol a hangnyomás megegyezik a referenciaszintével. Ez egy kis nyomás, de nem nulla. Lehetséges negatív hangszint is: – 20 dB olyan hangot jelentene, amelynek nyomása 10-szer kisebb, mint a referencianyomás, azaz 2 μPa.

Nem minden hangnyomás egyformán hangos. Ennek az az oka, hogy az emberi fül nem egyformán reagál minden frekvenciára: a körülbelül 1 kHz és 7 kHz közötti frekvenciatartományban (1000-7000 rezgés/másodperc) sokkal érzékenyebbek vagyunk a hangokra, mint a nagyon alacsony vagy magas frekvenciájú hangokra. Emiatt a hangmérőket általában olyan szűrővel szerelik fel, amelynek frekvenciaválasza egy kicsit hasonlít az emberi fül frekvenciaválaszához. (Ezekről a szűrőkről bővebben alább.) Ha az “A súlyozású szűrőt” használják, a hangnyomásszintet dB(A) vagy dBA egységben adják meg. A dBA-skálán mért hangnyomásszint könnyen mérhető, ezért széles körben használják. A hangerősségtől való eltérésének egyik oka, hogy a szűrő nem ugyanúgy reagál, mint a fül. Ahhoz, hogy megértsük egy hang hangosságát, először is konzultálnunk kell néhány, az emberi fül frekvenciaválaszát ábrázoló görbével, amelyeket az alábbiakban adunk meg. (Alternatívaként megmérheti a saját hallásválaszát.) Egy másik ok, hogy az emberi hallás nem logaritmikus.

Logaritmikus mértékegységek

Miért használunk decibeleket? A fül nagyon nagy hangtartományt képes meghallani: a rövid ideig tartó expozícióból eredő maradandó károsodást okozó hangnyomás és a (sérülésmentes) fül által hallható határérték aránya több mint egymillió. Egy ilyen tartomány kezeléséhez hasznosak a logaritmikus egységek: az egymillió logaritmusa 6, így ez az arány 120 dB különbséget jelent. A hallás nem eredendően logaritmikusan reagál. (A logaritmikus mértékegységek akkor is hasznosak, ha egy hang (rövid ideig) exponenciálisan nő vagy csökken az idő múlásával. Ez számos, arányos erősítéssel vagy arányos veszteséggel járó alkalmazásban fordul elő.)

A dBA és dB(C)

A legszélesebb körben használt hangszint-szűrő az A skála, amely nagyjából megfelel a 40 dB (1 kHz-en) egyenlő hangosságú görbe inverzének. Ezt a szűrőt használva a hangszintmérő így kevésbé érzékeny a nagyon magas és nagyon alacsony frekvenciákra. Az ezen a skálán végzett méréseket dBA-ban fejezzük ki. A C skála több oktávon keresztül kevéssé változik, ezért szubjektív mérésekre csak közepes és magas hangszintek esetén alkalmas. Az ezen a skálán végzett méréseket dB(C)-ben fejezzük ki. Létezik egy (ritkán használt) B súlyozási skála is, amely az A és a C között helyezkedik el. Az alábbi ábra az A szűrő (balra) és a C szűrő válaszát mutatja, a dB-ben megadott erősítésekkel 1 kHz-re vonatkoztatva. (A szűrőkbe való bevezetésért lásd: RC-szűrők, integrátorok és differenciálók).



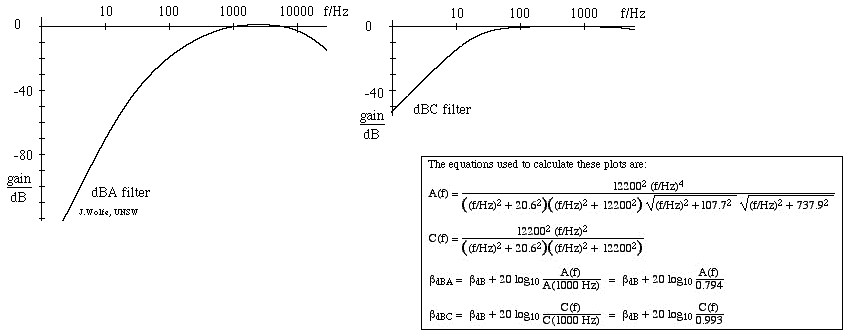
A zeneakusztika és a beszédakusztika oldalakon a hangspektrumokat dB-ben ábrázoljuk. Ennek a bevett gyakorlatnak az az oka, hogy a mért hangnyomás tartománya nagy.

A dB(G) mérések egy keskeny sávú szűrőt használnak, amely az 1 és 20 Hz közötti frekvenciákat nagy, a többi frekvenciát pedig kis súllyal súlyozza. Így nagy értékeket ad az olyan hangok és infrahangok esetében, amelyeket nem lehet könnyen hallani. ISO 7196:1995

Zaj, phon és sones, hallásválaszgörbék

A phon egy olyan mértékegység, amelyet a fül pszichofizikailag mért frekvenciaválasza viszonyít a dB-hez. 1 kHz-en a phonban és dB-ben mért értékek definíció szerint megegyeznek. Minden más frekvencia esetében a phon skálát olyan kísérletek eredményei határozzák meg, amelyekben önkénteseket arra kértek, hogy egy adott frekvenciájú jel hangerejét addig állítsák be, amíg annak hangerejét egy 1 kHz-es jel hangerejével azonosnak ítélték. A dB-ről phonra való átváltáshoz szükség van az ilyen eredmények grafikonjára. Egy ilyen grafikon a hangerősségtől függ: magas hangerősségnél laposabbá válik.

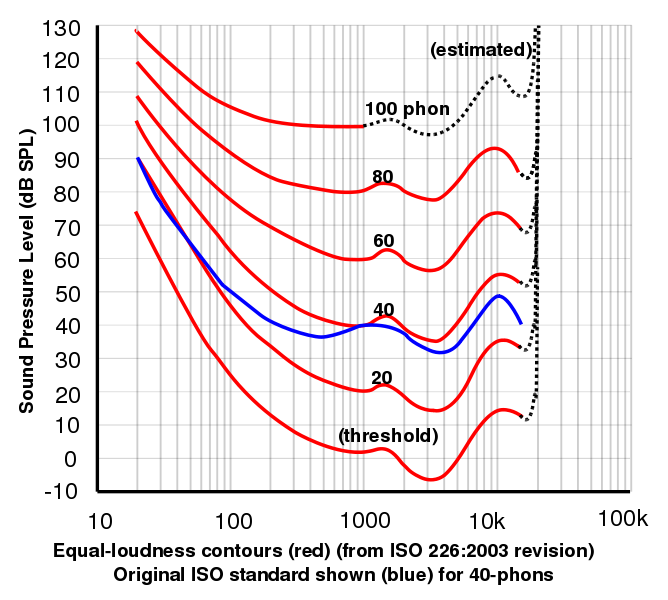
Ez a grafikon a Lindosland jóvoltából a Nemzetközi Szabványügyi Szervezet 2003-as adatait mutatja a kísérletileg meghatározott egyenlő hangossági görbékre vonatkozóan. Az egyenlő hangosság ábráit a frekvencia függvényében gyakran általánosan Fletcher-Munson-görbéknek nevezik Fletcher, H. és Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Saját görbéket készíthet a hallásválasz oldalunk segítségével.

A sone pszichofizikai mérésekből származik, amelyek során önkéntesek addig állították be a hangokat, amíg kétszer olyan hangosnak ítélték meg azokat. Ez lehetővé teszi, hogy az észlelt hangosságot a phone-hoz viszonyítsuk. Egy sone 40 phonnal egyenlő. Kísérletileg megállapították, hogy 40 phon felett a hangszint 10 dB-es növekedése körülbelül a hangerősség kétszeresének felel meg. Ezért ezt a közelítést használják a sone meghatározásánál: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon stb.



Ez a kapcsolat azt jelenti, hogy a hangerősség és az intenzitás között hatványtörvény áll fenn: a hangerősség szonokban kifejezve arányos (intenzitás)log 2 = (intenzitás)0,3 értékkel.

Nem lenne nagyszerű, ha át tudnánk számolni dB-ről (ami egy műszerrel mérhető) sones-re (ami megközelíti az emberek által érzékelt hangerőt)? Ez néha az akusztikai kézikönyvekben található táblázatok segítségével történik. Ha azonban nem bánja a meglehetősen durva közelítést, akkor azt mondhatjuk, hogy az A súlyozási görbe az emberi frekvenciaválaszhoz közelít alacsony és közepes hangszinteken, így a dB(A) nagyon nagyjából megegyezik a fonokkal, az alacsony hangszintek korlátozott tartományában. Ezután használhatjuk a fent leírt logaritmikus kapcsolatot a hangok és a phonok között.

Felvételi szint és decibelek

A hangelektronikai eszközökön (keverőpultok stb.) a felvételi vagy kimeneti szintet mérő mérők szinte mindig az AC effektív feszültséget rögzítik (lásd a linkeket az AC és az effektív értékek megismeréséhez). Egy adott R ellenállás esetén a P teljesítmény V2/R, tehát
feszültségszintkülönbség = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, vagy

abszolút feszültségszint = 20 log (V/Vref)

ahol Vref egy referenciafeszültség. Mi tehát a referenciafeszültség?

A nyilvánvalóan választott szint egy volt effektív érték, és ebben az esetben a szintet dBV-ként írjuk fel. Ez racionális, és kényelmes is az analóg-digitális kártyáknál, amelyek maximális tartománya gyakran körülbelül egy volt effektív értékű. Tehát nem szabad elfelejteni, hogy a szintet negatív dBV-ben (egy voltnál kisebb) tartsuk, hogy elkerüljük a jel csúcsainak levágását, de ne legyen túl negatív (így a jelünk még mindig sokkal nagyobb, mint a háttérzaj).

Néha dBm-t fog látni. Ez régebben az elektromos teljesítmény decibelét jelentette, egy milliwattra vonatkoztatva, és néha még mindig így van. Történelmi okokból azonban bonyolult. A huszadik század közepén sok hangvezeték névleges impedanciája 600 Ω. Ha az impedancia tisztán ellenállásos, és ha V2/600 Ω = 1 mW, akkor V = 0,775 voltot kapunk. Tehát, feltéve, hogy 600 Ω-os terhelést használt, 1 mW teljesítmény 0 dBm volt, ami 0,775 V, tehát így kalibrálta a szintmérőket. A probléma azért merült fel, mert ha egy feszültséget mérő szintmérő egyszer így van kalibrálva, akkor 0 dBm-t 0,775 V-nál fog leolvasni, még akkor is, ha nem 600 Ω-ra van csatlakoztatva. Így, talán logikátlanul, a dBm néha dB-t fog jelenteni 0,775 V-ra vonatkoztatva. (Gyerekkoromban a számológépek drágák voltak, ezért apa régi tolózárát használtam, amelynek kurzorablakán a 0,775 faktor volt jelölve az ilyen számítások megkönnyítésére.)

Hogyan lehet dBV-t vagy dBm-t dB hangerősséggé alakítani? Nincs egyszerű módszer. Attól függ, hogyan alakítjuk át az elektromos teljesítményt hangteljesítményre. Még akkor is, ha az elektromos jelet közvetlenül egy hangszóróhoz csatlakoztatja, az átalakítás a hangszóró hatásfokától és impedanciájától függ. És persze lehet egy teljesítményerősítő, és különböző akusztikai bonyodalmak aközött, ahol a keverőpulton a dBV-t méri, és aközött, ahol a füle a hangtérben van.

Intenzitás, sugárzás és dB

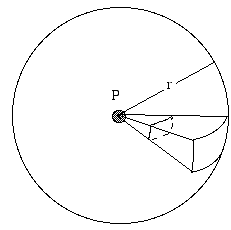
Hogyan függ a hangszint (vagy a rádiójelek szintje stb.) a forrástól való távolságtól?

Az olyan forrást, amely minden irányban egyformán bocsát ki sugárzást, izotrópnak nevezzük. Tekintsünk egy elszigetelt hangforrást, távol minden visszaverő felülettől – talán egy magasan a levegőben éneklő madár. Képzeljünk el egy r sugarú gömböt, amelynek középpontja a forrás. A forrás folyamatosan P összteljesítményt bocsát ki. Ez a hangteljesítmény szétterül és áthalad a gömb felületén. Ha a forrás izotróp, akkor az I intenzitás definíció szerint mindenhol azonos ezen a felületen. Az I intenzitást az egységnyi területre jutó teljesítményként határozzuk meg. A gömb felülete 4πr2, így az egyes négyzetméternyi felületen áthaladó teljesítmény (példánkban a hangteljesítmény) a definíció szerint:

I = P/4πr2.

Azt látjuk tehát, hogy izotróp forrás esetén az intenzitás fordítottan arányos a forrástól való távolság négyzetével:

I2/I1 = r12/r22.

Az intenzitás azonban arányos a hangnyomás négyzetével, így ugyanígy leírhatjuk:

p2/p1 = r1/r2.

Ha tehát megduplázzuk a távolságot, akkor a hangnyomást 2-szeresére, az intenzitást pedig 4-szeresére csökkentjük: más szóval a hangszintet 6 dB-lel csökkentjük. Ha r-t 10-szeresére növeljük, akkor 20 dB-lel csökkentjük a szintet, stb.

Vigyázzunk azonban, hogy sok forrás nem izotróp, különösen, ha a hullámhossz kisebb, vagy a forrással összehasonlítható méretű. Továbbá a visszaverődések gyakran igen fontosak, különösen, ha a talaj a közelben van, vagy ha beltérben vagyunk.

Nyomás, intenzitás és fajlagos impedancia

Akusztikus hullámok esetén a z fajlagos akusztikus impedanciát a p akusztikus nyomás és az u átlagos részecske sebesség hányadosaként határozzuk meg, a hang ave miatt, z = p/u . Az Akusztikai impedancia, intenzitás és teljesítmény című fejezetben bemutatjuk, hogyan lehet összefüggésbe hozni a p RMS akusztikai nyomást és az I intenzitást:
I = p2/z

A levegő esetében a z fajlagos akusztikai impedancia 420 kg.s-1.m-2 = 420 Pa.s.m-1. (Édes) víz esetében a víz fajlagos akusztikai impedanciája 1,48 MPa.s.m-1. Tehát egy azonos nyomású hanghullám a vízben sokkal kisebb intenzitású, mint a levegőben.

dBi és az irányban változó sugárzás

Az irányban változó sugárzást anizotrópnak nevezzük. A kommunikációban sok esetben az izotróp sugárzás pazarló: miért sugároznánk a teljesítmény jelentős részét felfelé, ha a vevő, hozzád hasonlóan, viszonylag közel van a talajszinthez. A rövid hullámhosszú hangok esetében (beleértve a beszéd szempontjából fontos tartomány nagy részét) egy megafon segíthet anizotrópabbá tenni a hangot. A rádiózás esetében a kialakítások széles skálája lehetővé teszi, hogy az antennák mind az adás, mind a vétel szempontjából erősen anizotrópikusak legyenek.

Amikor tehát egy adott irányban történő sugárzás (vagy vétel) érdekel, azt akarjuk, hogy az adott irányban, adott távolságban mért intenzitás aránya nagyobb legyen, mint egy izotróp sugárzótól ugyanilyen távolságban mért (vagy egy izotróp vevő által fogadott) intenzitás aránya. Ezt az arányt nevezzük erősítésnek; az arányt dB-ben fejezzük ki, és megkapjuk az adott sugárzó dBi-ben kifejezett erősítését. Ezt az egységet főként antennáknál használják, akár adó-, akár vevőantennáknál, de néha hangforrásoknál és irányított mikrofonoknál is alkalmazzák.

Példa problémák

Néhányan írtak, és példákat kértek a dB számításokban való használatára. Tehát…
• Minden más esetben egyenlő, mennyivel hangosabb egy 100 W-os erősítővel meghajtott hangszóró (a lineáris tartományban), mint egy 10 W-os erősítővel meghajtott hangszóró?

  A teljesítmények tízszeresen különböznek, ami, mint fentebb láttuk, 10 dB. Minden más egyenlő itt azt jelenti, hogy a frekvenciaválaszok egyenlőek, és hogy ugyanazt a bemeneti jelet használjuk, stb. Tehát a frekvenciafüggésnek azonosnak kell lennie. A 10 dB 10 phonnak felel meg. A hangerő érzékelt megduplázódásához 10 fonttal nagyobb hangerőre van szükség. Tehát a 100 W-os erősítővel meghajtott hangszóró kétszer olyan hangos, mint a 10 W-os erősítővel meghajtva, feltéve, hogy a lineáris tartományban marad, és nem torzítja vagy teszi tönkre a hangszórót. (A 100 W-os erősítő kétszer annyi hangot termel, mint a 10 W-os.)

• R távolságban állok egy kis hangforrástól (mérete jóval kisebb, mint R), a talajszinten, kint a szabadban, ahol a visszaverődések elhanyagolhatók. A hangszint L. Ha most elmegyek egy nR távolságba (n egy szám, és nR még mindig sokkal nagyobb, mint a forrás mérete), mekkora lesz az új hangszint?

  Először is jegyezzük meg, hogy a visszaverődések elhanyagolása nagyon fontos. Ez a számítás nem fog működni egy helyiségben, ahol a falról érkező (együttesen visszhangot előidéző) visszaverődések eléggé megnehezítik a számítást. A szabadban a hangintenzitás arányos 1/r2-vel, ahol r a forrástól mért távolság. (Az arányossági állandó attól függ, hogy a talaj mennyire verődik vissza, és minket itt nem érint, mert a számításban nagyjából ki fog egyenlítődni, feltéve, hogy r ésszerűen nagy). Ha tehát r-t R-ről nR-re növeljük, akkor az intenzitást I-ről I/n 2-re csökkentjük.

  A két I 2 és I 1 intenzitású jel közötti különbség decibelben kifejezve a fentiekben

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Ha például n 2 (azaz ha kétszer olyan messzire megyünk), akkor az intenzitás négyszeresére csökken, és a hangszint L-ről (L – 6dB) csökken.

• Ha ideális csendes körülmények között egy fiatal egy hangszóró (esetleg egy softspeaker?) által kibocsátott 1 kHz-es, 0 dB-es hangot hall, mennyivel kell növelni a hangszóró teljesítményét, hogy a hangot 110 dB-re (veszélyesen hangos, de túlélhető szintre) emeljük?

  A két P2 és P1 teljesítményű jel közötti decibelkülönbség a fenti definíció szerint

  ΔL = 10 log (P2/P1) dB, tehát a két egyenlő mennyiséget 10-re emelve:
  10L/10 = P2/P1 tehát:
  P2/P1 = 10110/10 = 1011 = százezermillió.

  ami azt bizonyítja, hogy az emberi fülnek feltűnően nagy dinamikai tartománya van, talán nagyobb, mint a szemé.

• Egy erősítő bemenete 10 mV, kimenete pedig 2 V. Mekkora a feszültségerősítése dB-ben kifejezve?

  A feszültség, akárcsak a nyomás, négyzetesen jelenik meg a teljesítmény vagy az intenzitás kifejezésekben. (Az R ellenállásban disszipált teljesítmény V2/R.) Így egyezményesen definiáljuk:

  erősítés = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (A fenti akusztikai esetekben láttuk, hogy a dB-ben kifejezett nyomásarány megegyezik a teljesítményaránnyal: ez volt az oka a 20-as tényezőnek, amikor a dB-t a nyomásra definiáltuk. Érdemes megjegyezni, hogy a feszültségerősítéses példában az erősítő teljesítményerősítése valószínűleg nem egyenlő a feszültségerősítéssel, amelyet az itt használt konvenció határoz meg. A teljesítmény arányos az adott ellenálláson lévő feszültség négyzetével. Az erősítők bemeneti és kimeneti impedanciája azonban gyakran meglehetősen eltérő. Például egy puffererősítő vagy emitterkövető körülbelül 1 feszültségerősítéssel, de nagy áramerősítéssel rendelkezik).

• Mekkora a különbség dB-ben a Földön (8,3 fénypercre a Naptól) és az Uránuszon (160 fénypercre) mért besugárzás (fényintenzitás) között?

  A hanghoz hasonlóan az izotróp fényintenzitás r-2-vel csökken, így az intenzitás aránya (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Munkahelyi egészségvédelem és biztonság

A különböző országokban és tartományokban nyilvánvalóan különböző törvények vonatkoznak a munkahelyi zajterhelésre, amelyeket eltérő lelkesedéssel hajtanak végre. Sok ilyen szabályozás 85 dB(A)-ban határozza meg a folyamatos zajterhelés határértékét egy 8 órás műszakra vonatkozóan. Minden 3 dB-es növekedés esetén a megengedett expozíció a felére csökken. Tehát, ha Ön egy éjszakai szórakozóhelyen dolgozik, ahol az erősített zene 100 dB(A) értéket produkál a füle közelében, a megengedett expozíció 15 perc. Van egy határérték az olyan impulzusszerű zajokra, mint a lőfegyverek vagy a robbanó lövedékeket használó szerszámok. (pl. a 140 dB csúcsértéket nem szabad túllépni a nap bármely szakában.) Számos dokumentum tartalmaz tanácsokat arra vonatkozóan, hogyan csökkenthető a zajexpozíció a forrásnál (azaz csökkentse a zene szintjét), a forrás és a fül között (azaz koncerteken távolodjon el a hangszóróktól) és a fülnél (azaz viseljen füldugót vagy ipari hallásvédőt). A zajkezelés és a munkahelyi hallásvédelem az ausztráliai Új-Dél-Wales állam (a szerző címe) gyakorlati kódexe.

Néhány GYIK

• Milyen hangos egy repülőgép? Egy vonat? Egy éneklő ember? Egy kutya ugatása? Egy elektromos szerszám? A válaszok erre a kérdésre nagyon eltérőek. Erősen függ attól, hogy milyen messze van, hogy beltérben van-e vagy sem, van-e visszhang, milyen erős az adott forrás és milyen a spektruma. Értékeket megadni anélkül, hogy nagyon konkrétan meghatároznánk a körülményeket, kissé félrevezető lenne. Mivel az oldal többi részének célja, hogy megbízható legyen, amennyire csak lehet, itt inkább nem adnék meg értékeket.
• Hogyan “adjuk össze a decibeleket”, azaz Milyen hangszintet kapunk, ha az a szintet hozzáadjuk a b szinthez? Ha a források koherensek (ami általában azt jelenti, hogy végső soron ugyanabból a forrásból származnak), akkor bonyolult interferenciahatások léphetnek fel. A legtöbb esetben, amikor a források függetlenek, összeadhatjuk az intenzitásokat, majd átszámíthatjuk őket decibelre. Ha azonban a hangszinteket dB(A)-ban adják meg, nem olyan egyszerű visszavezetni az intenzitásra, és tudnunk kell valamit a hang spektrumáról. Ha ismered a hang eloszlását a különböző frekvenciasávokban, akkor használhatod az ezen a linken található appletet.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.