Elektromágneses sugárzás
TheoryEdit
Maxwell-egyenletekSzerkesztés
James Clerk Maxwell levezette az elektromos és mágneses egyenletek hullámformáját, és ezzel felfedezte az elektromos és mágneses mezők hullámszerűségét és szimmetriáját. Mivel a hullámegyenlet által megjósolt EM-hullámok sebessége egybeesett a mért fénysebességgel, Maxwell arra a következtetésre jutott, hogy maga a fény is EM-hullám. Maxwell egyenleteit Heinrich Hertz rádióhullámokkal végzett kísérletek révén megerősítette.
A Maxwell-egyenletek szerint a térben változó elektromos térhez mindig társul egy időben változó mágneses tér. Hasonlóképpen, a térben változó mágneses mező az elektromos mező bizonyos időbeli változásaival jár együtt. Egy elektromágneses hullámban az elektromos mező változásai mindig az egyik irányban a mágneses mező hullámzásával járnak együtt, és fordítva. Ez a kettő közötti kapcsolat anélkül következik be, hogy bármelyik mezőtípus okozná a másikat; inkább együtt fordulnak elő, ugyanúgy, ahogyan az idő és a tér változásai együtt fordulnak elő és kapcsolódnak egymáshoz a speciális relativitáselméletben. Valójában a mágneses mezők tekinthetők elektromos mezőknek egy másik vonatkoztatási rendszerben, és az elektromos mezők tekinthetők mágneses mezőknek egy másik vonatkoztatási rendszerben, de jelentőségük azonos, mivel a fizika minden vonatkoztatási rendszerben ugyanaz, így a tér- és időváltozások közötti szoros kapcsolat itt több mint analógia. Ezek a mezők együttesen egy terjedő elektromágneses hullámot alkotnak, amely kimozdul a térbe, és soha többé nem kell kölcsönhatásba lépnie a forrással. A töltés gyorsulásával ily módon kialakuló távoli EM-mező energiát hordoz magában, amely “kisugárzik” a térben, innen a kifejezés.
Közeli és távoli mezőkSzerkesztés

Maxwell egyenletei megállapították, hogy egyes töltések és áramok (“források”) olyan helyi típusú elektromágneses mezőt hoznak létre a közelükben, amely nem az EMR viselkedésével rendelkezik. Az áramok közvetlenül mágneses teret hoznak létre, de ez mágneses dipólus típusú, amely az áramtól való távolsággal megszűnik. Hasonló módon a változó elektromos potenciál által egy vezetőben szétnyomott mozgó töltések (például egy antennában) elektromos dipólus típusú elektromos mezőt hoznak létre, de ez is csökken a távolsággal. Ezek a mezők alkotják a közeli mezőt az EMR-forrás közelében. Egyik viselkedés sem felelős az EM-sugárzásért. Ehelyett olyan elektromágneses mező viselkedést okoznak, amely csak a forráshoz nagyon közel lévő vevőnek ad át hatékonyan energiát, mint például a mágneses indukció egy transzformátorban, vagy a visszacsatolásos viselkedés, amely egy fémdetektor tekercsének közelében történik. Jellemzően a közeli mezők erőteljes hatást gyakorolnak saját forrásaikra, megnövekedett “terhelést” (csökkentett elektromos reaktanciát) okozva a forrásban vagy az adóban, valahányszor egy vevő energiát von el az EM-mezőből. Egyébként ezek a mezők nem “terjednek” szabadon a térben, energiájukat távolságkorlátozás nélkül elszállítva, hanem inkább oszcillálnak, energiájukat visszaadva az adónak, ha azt egy vevő nem veszi.
Az EM távoli mező ezzel szemben olyan sugárzásból áll, amely abban az értelemben mentes az adótól, hogy (ellentétben egy elektromos transzformátor esetével) az adónak ugyanannyi energiára van szüksége ahhoz, hogy ezeket a mezőváltozásokat kiküldje, függetlenül attól, hogy a jelet azonnal felveszik-e vagy sem. Az elektromágneses mezőnek ez a távoli része az “elektromágneses sugárzás” (más néven távoli mező). A távoli mezők terjednek (sugároznak) anélkül, hogy az adó hatással lenne rájuk. Ezáltal függetlenek abban az értelemben, hogy létezésük és energiájuk, miután elhagyták az adót, teljesen független mind az adótól, mind a vevőtől. Az energia megmaradása miatt a forrás köré rajzolt bármely gömbfelületen áthaladó teljesítmény mennyisége azonos. Mivel egy ilyen felület területe a forrástól való távolság négyzetével arányos, az EM-sugárzás teljesítménysűrűsége mindig a forrástól való távolság fordított négyzetével csökken; ezt nevezzük fordított négyzetes törvénynek. Ez ellentétben áll az EM-mező forráshoz közeli dipólusrészeivel (a közeli mezővel), amelyek teljesítménye a fordított kocka teljesítménytörvény szerint változik, és így nem konzervált energiamennyiséget szállítanak a távolságokon keresztül, hanem a távolsággal halványulnak, és energiájuk (mint említettük) gyorsan visszatér az adóhoz, vagy egy közeli vevő (például egy transzformátor szekunder tekercse) elnyeli azt.
A távoli mező (EMR) keletkezése más mechanizmustól függ, mint a közeli mezőé, és a Maxwell-egyenletek más kifejezései alapján. Míg a közeli mező mágneses része a forrásban lévő áramoknak köszönhető, addig az EMR-ben a mágneses mező csak az elektromos mező helyi változásának köszönhető. Hasonlóképpen, míg a közeli mező elektromos mezeje közvetlenül a forrásban lévő töltéseknek és töltésszétválásnak köszönhető, addig az EMR-ben az elektromos mező a helyi mágneses mező változásának köszönhető. Az elektromos és mágneses EMR-mezők előállításának mindkét folyamata másképpen függ a távolságtól, mint a közeli mező dipólusú elektromos és mágneses mező. Ezért válik az EMR típusú EM-mező dominánssá a forrásoktól “távol” lévő teljesítményben. A “forrástól távol” kifejezés arra utal, hogy a forrástól (fénysebességgel haladva) milyen messze van a kifelé mozgó EM-mező bármely része, mire a forrásáramokat a változó forráspotenciál megváltoztatja, és a forrás ezért elkezdett egy más fázisú, kifelé mozgó EM-mezőt létrehozni.
Az EMR tömörebb felfogása szerint az EMR-t alkotó távoli mező általában az EM-mezőnek az a része, amely a forrástól elegendő távolságot tett meg ahhoz, hogy teljesen elszakadjon az eredetileg érte felelős töltések és áramok visszacsatolásától. Most már független a forrás töltéseitől, az EM-mező, ahogy távolodik, csak az azt létrehozó töltések gyorsulásától függ. Nincs többé szoros kapcsolata a töltések közvetlen mezőivel vagy a töltések (áramok) sebességével.
Az egyetlen részecske mozgása következtében kialakuló elektromos és mágneses mezők Liénard-Wiechert-féle potenciálformulájában (a Maxwell-egyenletek szerint) a részecske gyorsulásával kapcsolatos kifejezések azok, amelyek a mező elektromágneses sugárzásnak tekintett részéért felelősek. Ezzel szemben a részecske változó statikus elektromos teréhez kapcsolódó kifejezés és a részecske egyenletes sebességéből eredő mágneses kifejezés mindkettő az elektromágneses közeli mezőhöz kapcsolódik, és nem tartozik az EM-sugárzáshoz.
PropertiesEdit

Az elektrodinamika az elektromágneses sugárzás fizikája, az elektromágnesesség pedig az elektrodinamika elméletéhez kapcsolódó fizikai jelenség. Az elektromos és mágneses mezők a szuperpozíció tulajdonságainak engedelmeskednek. Így egy adott részecskének vagy időben változó elektromos vagy mágneses térnek tulajdonítható mező hozzájárul az ugyanabban a térben más okok miatt jelenlévő mezőkhöz. Továbbá, mivel ezek vektormezők, minden mágneses és elektromos mező vektora összeadódik a vektoros összeadásnak megfelelően. Az optikában például két vagy több koherens fényhullám kölcsönhatásba léphet egymással, és konstruktív vagy destruktív interferencia révén olyan eredő besugárzást eredményezhet, amely eltér az egyes fényhullámok sugárzási összetevőinek összegétől.
A fény elektromágneses tereit nem befolyásolja, ha egy lineáris közegben, például vákuumban statikus elektromos vagy mágneses mezőkön halad át. Nemlineáris közegekben azonban, mint például egyes kristályokban, kölcsönhatások léphetnek fel a fény és a statikus elektromos és mágneses mezők között – e kölcsönhatások közé tartozik a Faraday-effektus és a Kerr-effektus.
A fénytörés során az egyik közegből egy másik, eltérő sűrűségű közegbe átjutó hullám az új közegbe belépve megváltoztatja sebességét és irányát. A közegek törésmutatóinak aránya határozza meg a törés mértékét, amit a Snell-törvény foglal össze. Az összetett hullámhosszúságú fény (természetes napfény) egy prizmán áthaladva látható spektrumra oszlik szét a prizma anyagának hullámhosszfüggő törésmutatója miatt (diszperzió), vagyis az összetett fényben az egyes komponens hullámok különböző mértékben hajlanak meg.
Az EM-sugárzás egyszerre mutat hullám- és részecsketulajdonságokat (lásd hullám-részecske dualitás). Mind a hullám-, mind a részecskejellemzőket számos kísérletben igazolták. A hullámtulajdonságok jobban megmutatkoznak, ha az EM-sugárzást viszonylag nagy időskálán és nagy távolságokon mérjük, míg a részecsketulajdonságok inkább kis időskálák és távolságok mérésekor válnak nyilvánvalóvá. Például, amikor az elektromágneses sugárzást elnyeli az anyag, a részecskejellegű tulajdonságok sokkal nyilvánvalóbbak lesznek, ha a fotonok átlagos száma az adott hullámhossz kockájában sokkal kisebb, mint 1. Nem olyan nehéz kísérletileg megfigyelni az energia nem egyenletes lerakódását a fény elnyelésekor, azonban ez önmagában nem bizonyíték a “részecske” viselkedésre. Inkább az anyag kvantumtermészetét tükrözi. Annak bizonyítása, hogy maga a fény kvantált, nem csupán az anyaggal való kölcsönhatása, már sokkal finomabb dolog.
Egyes kísérletek az elektromágneses hullámok hullám- és részecskejellegét is megmutatják, mint például az egyetlen foton öninterferenciája. Amikor egyetlen fotont küldünk át egy interferométeren, az mindkét útvonalon áthalad, interferál önmagával, ahogy a hullámok is teszik, mégis egy fotomultiplier vagy más érzékeny detektor csak egyszer érzékeli.
Az elektromágneses sugárzás és az anyag, például az elektronok közötti kölcsönhatást a kvantumelektrodinamika elmélete írja le.
Az elektromágneses hullámok polarizálódhatnak, visszaverődhetnek, megtörhetnek, meghajolhatnak vagy interferálhatnak egymással.
HullámmodellEdit

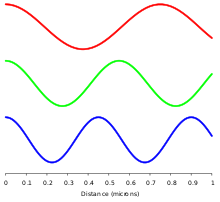
Homogén, izotróp közegben az elektromágneses sugárzás transzverzális hullám, ami azt jelenti, hogy rezgései merőlegesek az energiaátvitel és a terjedés irányára. A mező elektromos és mágneses része fix erősségarányban áll, hogy teljesüljön a két Maxwell-egyenlet, amely meghatározza, hogyan keletkezik az egyik a másikból. Disszipációmentes (veszteségmentes) közegekben ezek az E- és B-mezők is fázisban vannak, és mindkettő a tér azonos pontjain éri el a maximumot és a minimumot (lásd az ábrákat). Gyakori tévhit, hogy az E és B mezők az elektromágneses sugárzásban fázison kívüliek, mert az egyik változása a másikat is előidézi, és ez szinuszos függvényként fáziskülönbséget eredményezne közöttük (ahogyan ez az elektromágneses indukcióban és az antennákhoz közeli közeli mezőben valóban előfordul). A távoli mező elektromágneses sugárzásában azonban, amelyet a két forrás nélküli Maxwell-féle görbeoperátor-egyenlet ír le, helyesebb leírás az, hogy az egyik típusú mező időbeli változása arányos a másik típusú mező térbeli változásával. Ezek a deriváltak megkövetelik, hogy az E és B mezők az EMR-ben fázisban legyenek (lásd a matematikai részt alább).
A fény természetének fontos aspektusa a frekvenciája. A hullám frekvenciája a hullám rezgésszámát jelenti, és hertz-ben, a frekvencia SI-egységében mérik, ahol egy hertz másodpercenként egy rezgésnek felel meg. A fénynek általában több frekvenciája van, amelyek összegződve alkotják az eredő hullámot. A különböző frekvenciák különböző fénytörési szögeket érnek el, ezt a jelenséget diszperziónak nevezzük.
A monokromatikus hullám (egyetlen frekvenciájú hullám) egymást követő hullámvölgyekből és hullámhegyekből áll, és a két szomszédos hullámhegy vagy hullámvölgy közötti távolságot nevezzük hullámhossznak. Az elektromágneses spektrum hullámai különböző méretűek, a nagyon hosszú, egy kontinensnél hosszabb rádióhullámoktól a nagyon rövid, az atommagoknál kisebb gammasugarakig. A frekvencia fordítottan arányos a hullámhosszal, az egyenlet szerint:
v = f λ {\displaystyle \displaystyle v=f\lambda }

ahol v a hullám sebessége (vákuumban c, más közegekben kisebb), f a frekvencia és λ a hullámhossz. Ahogy a hullámok átlépik a különböző közegek közötti határokat, sebességük megváltozik, de frekvenciájuk állandó marad.
A szabad térben az elektromágneses hullámoknak a Maxwell-féle elektromágneses hullámegyenlet megoldásainak kell lenniük. A megoldások két fő osztálya ismert, nevezetesen a síkhullámok és a gömbhullámok. A síkhullámok a gömbhullámok határesetének tekinthetők a forrástól való nagyon nagy (ideális esetben végtelen) távolságban. Mindkét hullámtípus hullámformája tetszőleges időfüggvény lehet (amennyiben kellően differenciálható, hogy megfeleljen a hullámegyenletnek). Mint minden időfüggvényt, ezt is fel lehet bontani Fourier-analízissel a frekvenciaspektrumára, illetve az egyes szinuszos összetevőkre, amelyek mindegyike egyetlen frekvenciát, amplitúdót és fázist tartalmaz. Az ilyen komponensű hullámot monokromatikusnak mondjuk. Egy monokromatikus elektromágneses hullámot a frekvenciájával vagy hullámhosszával, csúcsamplitúdójával, valamilyen referenciafázishoz viszonyított fázisával, terjedési irányával és polarizációjával lehet jellemezni.
Az interferencia két vagy több hullám szuperpozíciója, amely új hullámmintázatot eredményez. Ha a mezők komponensei azonos irányúak, akkor konstruktívan interferálnak, míg az ellentétes irányúak destruktív interferenciát okoznak. Az EMR által okozott interferenciára példa az elektromágneses interferencia (EMI) vagy közismertebb nevén a rádiófrekvenciás interferencia (RFI). Ezenkívül több polarizációs jel kombinálható (azaz interferálhat), hogy új polarizációs állapotokat hozzon létre, amit párhuzamos polarizációs állapotok létrehozásának nevezünk.
Az elektromágneses hullámok energiáját néha sugárzási energiának is nevezik.
Részecskemodell és kvantumelméletSzerkesztés
A 19. század végén egy anomália merült fel, amely a fény hullámelmélete és a fekete testeknek nevezett termikus sugárzók által kibocsátott elektromágneses spektrumok mérései közötti ellentmondást jelentette. A fizikusok hosszú évekig sikertelenül küzdöttek ezzel a problémával. Később az ultraibolya-katasztrófa néven vált ismertté. 1900-ban Max Planck kidolgozta a fekete testek sugárzásának új elméletét, amely megmagyarázta a megfigyelt spektrumot. Planck elmélete azon az elképzelésen alapult, hogy a fekete testek a fényt (és más elektromágneses sugárzást) csak diszkrét energiakötegek vagy energiacsomagok formájában bocsátják ki. Ezeket a csomagokat kvantumoknak nevezték. Albert Einstein 1905-ben azt javasolta, hogy a fénykvantumokat tekintsük valódi részecskéknek. Később a fényrészecske a foton nevet kapta, hogy megfeleljen más, ekkoriban leírt részecskéknek, például az elektronnak és a protonnak. A foton energiája, E, arányos a frekvenciájával, f, az alábbiak szerint
E = h f = h c λ {\displaystyle E=hf={\frac {hc}{\lambda }}\,\!}\,\!}

ahol h a Planck-állandó, λ {\displaystyle \lambda }

a hullámhossz, c pedig a fénysebesség. Ezt néha Planck-Einstein-egyenletnek is nevezik. A kvantumelméletben (lásd első kvantálás) a fotonok energiája tehát egyenesen arányos az EMR hullám frekvenciájával.
Hasonlóképpen a foton p impulzusa is arányos a frekvenciájával és fordítottan arányos a hullámhosszával:
p = E c = h f c = h λ . {\displaystyle p={E \over c}={h f \over c}={h \over \lambda }.}

A forrása Einstein javaslatának, hogy a fény részecskékből áll (vagy bizonyos körülmények között részecskeként viselkedhet), egy olyan kísérleti anomália volt, amelyet a hullámelmélet nem magyarázott meg: a fotoelektromos hatás, amelyben a fémfelületre érkező fény elektronokat taszított ki a felületről, ami elektromos áramot eredményezett egy alkalmazott feszültségen keresztül. Kísérleti mérések kimutatták, hogy az egyes kilökött elektronok energiája arányos volt a fény frekvenciájával, nem pedig az intenzitásával. Továbbá, egy bizonyos minimális frekvencia alatt, amely az adott fémtől függött, az intenzitástól függetlenül nem folyt áram. Ezek a megfigyelések ellentmondani látszottak a hullámelméletnek, és a fizikusok évekig hiába próbáltak magyarázatot találni rá. Einstein 1905-ben a fény részecskeelméletének feltámasztásával magyarázta meg ezt a rejtélyt, hogy megmagyarázza a megfigyelt hatást. Mivel azonban a bizonyítékok túlnyomó része a hullámelmélet mellett szólt, Einstein elképzeléseit kezdetben nagy szkepticizmus fogadta a befutott fizikusok körében. Végül Einstein magyarázatát elfogadták, mivel a fény új, részecske-szerű viselkedését figyelték meg, például a Compton-effektust.
Amint egy foton elnyelődik egy atomban, gerjeszti az atomot, és egy elektront magasabb energiaszintre emel (amely átlagosan távolabb van az atommagtól). Amikor egy elektron egy gerjesztett molekulában vagy atomban alacsonyabb energiaszintre süllyed, az energiakülönbségnek megfelelő frekvenciájú fényfotonokat bocsát ki. Mivel az atomok elektronjainak energiaszintjei diszkrétek, minden egyes elem és molekula a maga jellegzetes frekvenciáit bocsátja ki és nyeli el. Az azonnali fotonemissziót fluoreszcenciának, a fotolumineszcencia egyik típusának nevezzük. Erre példa a fluoreszkáló festékek által kibocsátott látható fény, amely ultraibolya fényre (fekete fényre) reagál. A látható fénytől eltérő spektrális sávokban számos más fluoreszcens emisszió is ismert. A késleltetett emissziót foszforeszcenciának nevezzük.
Hullám-részecske kettősségSzerkesztés
A fény természetét magyarázó modern elmélet tartalmazza a hullám-részecske kettősség fogalmát. Általánosabban fogalmazva az elmélet azt állítja, hogy mindennek van részecske- és hullámtermészete is, és különböző kísérletekkel ki lehet hozni az egyiket vagy a másikat. A részecskenyészet könnyebben kimutatható egy nagy tömegű tárgy segítségével. Louis de Broglie 1924-ben tett merész felvetése vezette rá a tudományos közösséget, hogy az anyag (pl. az elektronok) is hullám-részecske kettősséget mutat.
Az elektromágneses sugárzás hullám- és részecskehatásaSzerkesztés
A hullám- és részecskehatás együttesen teljes mértékben megmagyarázza az EM-sugárzás emissziós és abszorpciós spektrumát. Annak a közegnek az anyagösszetétele, amelyen a fény áthalad, meghatározza az abszorpciós és emissziós spektrum jellegét. Ezek a sávok megfelelnek az atomok megengedett energiaszintjeinek. Az abszorpciós spektrum sötét sávjai a forrás és a megfigyelő között lévő közegben lévő atomoknak köszönhetőek. Az atomok elnyelik a fény bizonyos frekvenciáit a kibocsátó és a detektor/szem között, majd minden irányban kibocsátják azokat. A detektor számára sötét sáv jelenik meg a sugárnyalábból szórt sugárzás miatt. Például egy távoli csillag által kibocsátott fényben a sötét sávokat a csillag légkörében lévő atomok okozzák. Hasonló jelenség fordul elő az emisszió esetében is, amely akkor látható, amikor egy kibocsátó gáz izzik az atomok bármilyen mechanizmustól – beleértve a hőt is – származó gerjesztése miatt. Ahogy az elektronok alacsonyabb energiaszintekre süllyednek, olyan spektrumot bocsátanak ki, amely az elektronok energiaszintjei közötti ugrásokat reprezentálja, de vonalak is láthatók, mert a gerjesztés után ismét csak bizonyos energiáknál történik emisszió. Erre példa a ködök emissziós spektruma. A gyorsan mozgó elektronok akkor gyorsulnak fel a legélesebben, amikor egy erőterülettel találkoznak, így a természetben megfigyelhető legmagasabb frekvenciájú elektromágneses sugárzás nagy részének előállításáért ők felelősek.
Ezek a jelenségek különböző kémiai meghatározásokat segíthetnek a hátulról megvilágított gázok (abszorpciós spektrumok) és az izzó gázok (emissziós spektrumok) összetételének meghatározásában. A spektroszkópia (például) meghatározza, hogy milyen kémiai elemekből áll egy adott csillag. A spektroszkópiát egy csillag távolságának meghatározására is használják a vöröseltolódás segítségével.
Terjedési sebességSzerkesztés
Amikor bármely vezeték (vagy más vezető tárgy, például antenna) váltakozó áramot vezet, az elektromágneses sugárzás az árammal azonos frekvencián terjed. Sok ilyen helyzetben azonosítható egy elektromos dipólusmomentum, amely a töltéseknek a gerjesztő elektromos potenciál miatti szétválásából keletkezik, és ez a dipólusmomentum időben oszcillál, ahogy a töltések oda-vissza mozognak. Ez az oszcilláció egy adott frekvencián változó elektromos és mágneses tereket hoz létre, amelyek aztán mozgásba hozzák az elektromágneses sugárzást.
Kvantumszinten elektromágneses sugárzás akkor keletkezik, amikor egy töltött részecske hullámcsomagja oszcillál vagy más módon felgyorsul. A helyhez kötött állapotban lévő töltött részecskék nem mozognak, de az ilyen állapotok szuperpozíciója olyan átmeneti állapotot eredményezhet, amelynek elektromos dipólusmomentuma időben oszcillál. Ez az oszcilláló dipólusmomentum felelős a töltött részecskék kvantumállapotai közötti sugárzásos átmenet jelenségéért. Ilyen állapotok fordulnak elő (például) az atomokban, amikor fotonok sugárzása történik, miközben az atom egyik stacionárius állapotból a másikba lép át.
A fényt mint hullámot sebesség (a fénysebesség), hullámhossz és frekvencia jellemzi. Részecskeként a fény fotonok áramlása. Mindegyiknek a hullám frekvenciájához viszonyított energiája van, amelyet a Planck-féle E = hf összefüggés ad meg, ahol E a foton energiája, h a Planck-állandó, 6,626 × 10-34 J-s, f pedig a hullám frekvenciája.
Egy szabályt a körülményektől függetlenül betartunk: Az EM-sugárzás vákuumban a megfigyelőhöz képest fénysebességgel terjed, függetlenül a megfigyelő sebességétől. (Ez a megfigyelés vezetett Einstein speciális relativitáselméletének kidolgozásához.) Közegben (a vákuumtól eltérő közegben) a frekvenciától és az alkalmazástól függően a sebességtényezőt vagy a törésmutatót veszik figyelembe. Mindkettő a közegben lévő sebességnek a vákuumban lévő sebességhez viszonyított aránya.
Speciális relativitáselméletSzerkesztés
A XIX. század végére különböző kísérleti anomáliákat nem lehetett megmagyarázni az egyszerű hullámelmélettel. Az egyik ilyen anomália a fénysebességgel kapcsolatos vitát érintette. A fény és más elektromágneses hullámok Maxwell egyenletei által megjósolt sebessége nem jelent meg, hacsak az egyenleteket nem módosították az először FitzGerald és Lorentz által javasolt módon (lásd a speciális relativitáselmélet története), vagy máskülönben ez a sebesség attól függött volna, hogy a megfigyelő milyen sebességgel viszonyul a “közeghez” (az úgynevezett világító éterhez), amely állítólag “hordozta” az elektromágneses hullámot (a levegő hanghullámok hordozásához hasonló módon). A kísérletek nem találtak megfigyelői hatást. 1905-ben Einstein azt javasolta, hogy a tér és az idő a fény terjedése és minden más folyamat és törvény szempontjából sebességváltoztatható egységnek tűnik. Ezek a változások magyarázzák a fénysebesség és az összes elektromágneses sugárzás állandóságát minden megfigyelő – még a relatív mozgásban lévők – szemszögéből is.