Marginális eloszlás

Valószínűségi eloszlások > Marginális eloszlás

Mi az a marginális eloszlás?

Nézze meg a videót vagy olvassa el az alábbi cikket:

A technikai definíciót kissé észbontó lehet nézegetni:

A határeloszlás definíciója = Ha X és Y diszkrét véletlen változók és f (x,y) a
együttes valószínűségeloszlásuk értéke (x,y) pontban (x,y), a függvények által adott:
g(x) = Σy f (x,y) és h(y) = Σx f (x,y) az X és Y határeloszlásai.

Ha jól bánsz az egyenletekkel, valószínűleg csak ennyit kell tudnod. Ez megmondja, hogyan találhatod meg a határeloszlást. De ha ez a képlet fejfájást okoz (ami a legtöbb embernek igen!), akkor használhatsz egy gyakorisági eloszlási táblázatot a határeloszlás megtalálására.

A határeloszlás onnan kapta a nevét, hogy a valószínűségeloszlási táblázat margóján jelenik meg.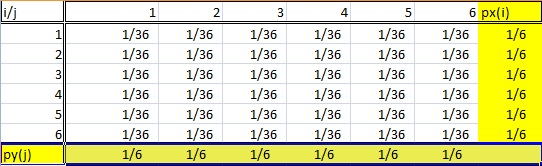

Az egész persze nem ilyen egyszerű. Nem lehet csak úgy megnézni bármilyen régi gyakorisági eloszlási táblázatot, és azt mondani, hogy az utolsó oszlop (vagy sor) egy “határeloszlás”. A határeloszlások néhány szabályt követnek:

• Az eloszlásnak kétváltozós adatokból kell származnia. A kétváltozós csak egy másik kifejezés arra, hogy “két változó”, például X és Y. A fenti táblázatban az i és j véletlen változók két kockadobásból származnak.
• A határeloszlás az, ahol csak az egyik véletlen változó érdekel . Más szóval, vagy X vagy Y. Ha megnézzük a fenti valószínűségi táblázatot, az egyik változó összegvalószínűségei az alsó sorban, a másik összegvalószínűségei pedig a jobb oldali oszlopban szerepelnek. Tehát ez a táblázat két határeloszlással rendelkezik.

Különbség a határeloszlás és a feltételes eloszlás között.

A feltételes eloszlás az, amikor a teljes adathalmazunknak csak egy bizonyos részhalmaza érdekel bennünket. A kockadobási példában ez lehet a “kettes dobás” vagy a “hatos dobás”. Az alábbi képen két kiemelt részpopuláció (és így két feltételes eloszlás) látható.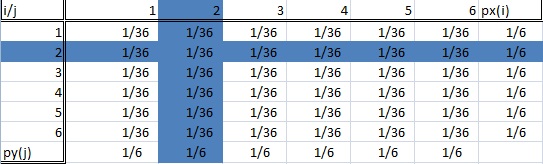

Hogyan számítsuk ki a határeloszlás valószínűségét

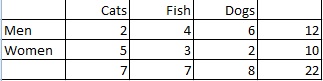
Példa kérdés: Számítsuk ki a háziállat-preferencia határeloszlását a férfiak és a nők körében:
Megoldás:
1. lépés: Számoljuk meg az emberek összlétszámát. Ebben az esetben a jobb oldali oszlopban szerepel az összlétszám (22 ember).
2. lépés: Számold meg az egyes háziállattípusokat preferáló emberek számát, majd az arányt alakítsd át valószínűséggé:
A macskákat preferáló emberek: 7/22 = .32
A halakat preferáló emberek: 7/22 = .32
A kutyákat preferáló emberek: 8/22 = .36
Tipp: A válaszodat úgy ellenőrizheted, hogy a valószínűségek összege mind 1.

2. példakérdés (kölcsönösen kizáró események): Ha P(A) = 0,20, P(b) = 0,70, és mindkét esemény kölcsönösen kizárja egymást, találd meg P(B’∩A), P(B’∩A’) és P(B∩A’).
Ha nem ismered ezt a jelölést, P(A’) azt jelenti, hogy “nem A”, vagy a komplementer. P(B’∩A) azt jelenti, hogy “a nem B és A metszete”).

Válasz:
A valószínűségeket egyenként is kiszámolhatod, de sokkal könnyebb kiszámolni őket egy táblázat segítségével.

1. lépés: Tölts ki egy gyakorisági táblázatot a megadott információkkal. A teljes valószínűségnek egyenlőnek kell lennie 1-gyel, így ezt is hozzáadhatod a margókhoz(összegekhez). Az egyszerű összeadás/algebra kitölti a marginális üres helyeket. Például az alsó sorban 0,70 + x = 1,00, így a B’ marginális összegének 0,30-nak kell lennie.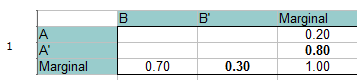

2. lépés: Adj hozzá 0-t A és B metszéspontjához, a táblázat bal felső részén. Ezt azért teheted meg, mert A és B kölcsönösen kizárják egymást, és nem fordulhatnak elő együtt.

3. lépés: Töltsd ki a többi üres részt egyszerű összeadással/algebra segítségével.

A táblázatból olvasva (nézd meg a két megadott valószínűség metszéspontjait):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Példa kérdés 3 (független események): Ha P(A) = 0,20, P(b) = 0,70, és mindkét esemény független, akkor találjuk meg P(B’∩A), P(B’∩A’) és P(B∩A’).

Válasz: Ha P(A) = 0,20, P(b) = 0,70, és mindkét esemény független, akkor találjuk meg P(B’∩A), P(B’∩A’) és P(B∩A’): Ezúttal A és B függetlenek, tehát annak a valószínűsége, hogy mindkettő egyszerre történik, 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Ez az érték a bal felső részbe kerül (A és B metszéspontja). A táblázat többi részét pontosan ugyanúgy töltsd ki, mint a fenti lépésekben.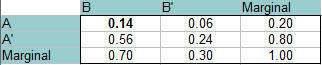

A táblázatból olvasd ki a válaszokat (a két valószínűség metszéspontjából):
P(B’∩A): 0.06
P(B’∩A’): 0,24
P(B∩A’): 0,56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 és 571, 2002.
Agresti A. (1990) Kategorikus adatelemzés. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2. kiadás. McGraw-Hill Education

——————————————————————————

Segítségre van szüksége egy házi feladathoz vagy tesztkérdéshez? A Chegg Study segítségével lépésről lépésre megoldásokat kaphat kérdéseire a terület szakértőjétől. Az első 30 perc egy Chegg oktatóval ingyenes!