Mi a kernel trükk? Miért fontos?

Amikor a gépi tanulásban a kernelekről beszélünk, valószínűleg először a támogató vektor gépek (SVM) modell jut eszünkbe, mivel a kernel trükk széles körben használatos az SVM modellben a linearitás és a nemlinearitás áthidalására.

Azért, hogy megértsd, mi az a kernel és miért fontos, először bemutatom az SVM modell alapjait.

Az SVM modell egy felügyelt gépi tanulási modell, amelyet elsősorban osztályozásra használnak (de regresszióra is lehet használni!). A döntési határok kialakításával tanulja meg a különböző csoportok elkülönítését.

A fenti grafikonon látható, hogy két megfigyelési osztály van: A kék pontok és a lila pontok. Ezt a két osztályt rengetegféleképpen szét lehet választani, ahogy a bal oldali grafikonon is látható. Mi azonban azt a “legjobb” hipersíkot szeretnénk megtalálni, amely maximalizálni tudja a két osztály közötti margót, ami azt jelenti, hogy a hipersík és a két oldalon lévő legközelebbi adatpontok közötti távolság a legnagyobb. Attól függően, hogy egy új adatpont a hipersík melyik oldalán helyezkedik el, egy osztályt rendelhetünk az új megfigyeléshez.

A fenti példában ez egyszerűen hangzik. Azonban nem minden adat szeparálható lineárisan. Valójában a való világban szinte minden adat véletlenszerűen eloszlik, ami megnehezíti a különböző osztályok lineáris elválasztását.

Miért fontos a kernel trükk használata?

Amint a fenti képen is látható, ha megtaláljuk a módját annak, hogy az adatokat 2 dimenziós térből 3 dimenziós térbe képezzük le, akkor olyan döntési felületet találunk, amely egyértelműen elválasztja a különböző osztályokat. Az első gondolatom ezzel az adattranszformációs folyamattal kapcsolatban az, hogy az összes adatpontot leképezzük egy magasabb dimenzióba (ebben az esetben 3 dimenzióba), megtaláljuk a határt, és elvégezzük az osztályozást.

Ez jól hangzik. Azonban amikor egyre több és több dimenzió van, az ezen a téren belüli számítások egyre drágábbak lesznek. Ekkor jön a képbe a kernel-trükk. Ez lehetővé teszi, hogy az eredeti jellemzőtérben operáljunk anélkül, hogy az adatok koordinátáit egy magasabb dimenziós térben számolnánk ki.

Nézzünk egy példát:

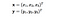
Itt x és y két adatpont 3 dimenzióban. Tegyük fel, hogy x-et és y-t le kell képeznünk a 9 dimenziós térben. A következő számításokat kell elvégeznünk, hogy megkapjuk a végeredményt, ami csak egy skalár. A számítási bonyolultság ebben az esetben O(n²).

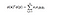
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).

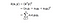
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Bármilyen, az (x, y) pontterméket tartalmazó számításban felhasználható a kernel-trükk.

A különböző kernelfüggvények

Vannak különböző kernelek. A legnépszerűbbek a polinomiális kernel és a radial basis function (RBF) kernel.

“Intuitív módon a polinomiális kernel nem csak a bemeneti minták adott jellemzőit vizsgálja a hasonlóságuk meghatározásához, hanem ezek kombinációit is” (Wikipedia), akárcsak a fenti példában. Az n eredeti jellemző és d fokú polinom esetén a polinomiális kernel n^d kiterjesztett jellemzőt eredményez.

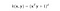
Az RBF kernelt Gauss kernelnek is nevezik. Végtelen számú dimenziója van a jellemzőtérnek, mert a Taylor-sorozattal bővíthető. Az alábbi formátumban a γ paraméter határozza meg, hogy mekkora befolyással bír egyetlen képzési példa. Minél nagyobb, annál közelebb kell lennie a többi példának ahhoz, hogy hatással legyen (sklearn dokumentáció).

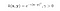
A Python sklearn könyvtárban különböző lehetőségek vannak a kernel függvények számára. Szükség esetén akár saját kernelt is készíthetünk.

A vég

A kernel trükk “tökéletes” tervnek hangzik. Azonban egy kritikus dolog, amit szem előtt kell tartanunk, hogy amikor az adatokat magasabb dimenzióra képezzük le, fennáll az esélye annak, hogy túlillesztjük a modellt. Ezért a megfelelő kernelfüggvény (beleértve a megfelelő paramétereket is) és a regularizáció kiválasztása nagy jelentőséggel bír.

Ha kíváncsi vagy arra, hogy mi az a regularizáció, írtam egy cikket, amiben az én felfogásomról beszélek, és itt találod.

Remélem, tetszett a cikk. Mint mindig, kérem, tudassa velem, ha bármilyen kérdése, megjegyzése, javaslata stb. van. Köszönöm az olvasást 🙂