Mi az aluláteresztő szűrő? Egy bemutató a passzív RC szűrők alapjairól
Mi a szűrés? Ismerje meg, hogy mik az ellenállás-kondenzátor (RC) aluláteresztő szűrők, és hol használhatja őket.
Ez a cikk bemutatja a szűrés fogalmát, és részletesen elmagyarázza az ellenállás-kondenzátor (RC) aluláteresztő szűrők célját és jellemzőit.
Az időtartomány és a frekvenciatartomány
Amikor egy elektromos jelet néz egy oszcilloszkópon, egy vonalat lát, amely a feszültség időbeli változását mutatja. Az idő bármely adott pillanatában a jelnek csak egy feszültségértéke van. Amit az oszcilloszkópon lát, az a jel időtartománybeli ábrázolása.
A tipikus oszcilloszkópos nyomvonal egyszerű és intuitív, de némileg korlátozó is, mivel nem mutatja meg közvetlenül a jel frekvenciatartalmát. Az időtartománybeli ábrázolással ellentétben, amelyben egy időpillanat csak egy feszültségértéknek felel meg, a frekvenciatartománybeli ábrázolás (más néven spektrum) az egyidejűleg jelen lévő különböző frekvenciakomponensek azonosításával közvetít információt a jelről.


Egy szinusz (fent) és egy négyszöghullám (lent) időtartománybeli ábrázolása.

A szinuszoid (fent) és a négyszöghullám (lent) frekvenciatartománybeli ábrázolásai.
Mi a szűrő?
A szűrő olyan áramkör, amely eltávolítja, azaz “kiszűri” a frekvenciakomponensek egy meghatározott tartományát. Más szóval, szétválasztja a jel spektrumát átmenő és blokkolt frekvenciakomponensekre.
Ha nincs sok tapasztalata a frekvenciatartománybeli analízissel kapcsolatban, még mindig bizonytalan lehet abban, hogy mik ezek a frekvenciakomponensek, és hogyan léteznek együtt egy olyan jelben, amelynek nem lehet egyszerre több feszültségértéke. Nézzünk egy rövid példát, amely segít tisztázni ezt a fogalmat.
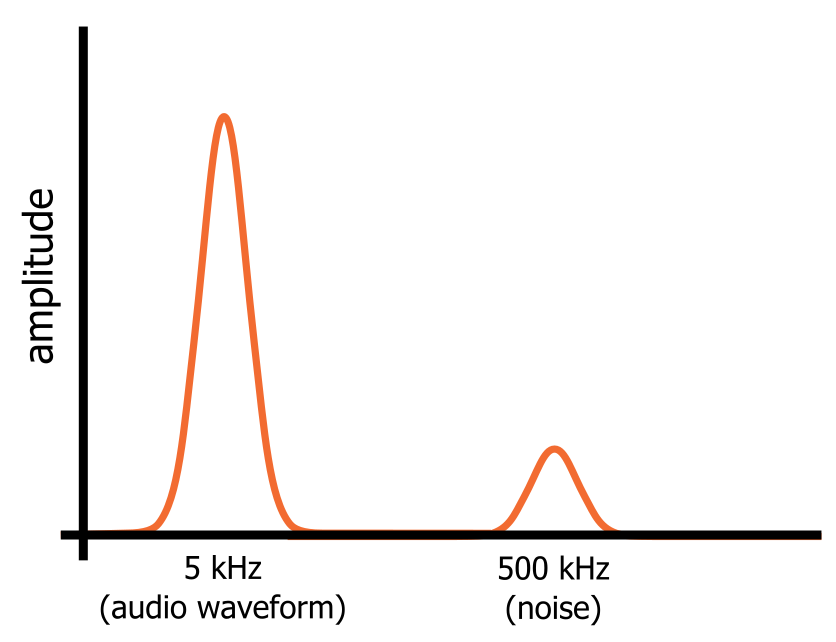
Tegyük fel, hogy van egy hangjelünk, amely egy tökéletes 5 kHz-es szinuszhullámból áll. Tudjuk, hogyan néz ki egy szinuszhullám az időtartományban, és a frekvenciatartományban nem látunk mást, mint egy frekvencia “tüskét” 5 kHz-en. Most tegyük fel, hogy aktiválunk egy 500 kHz-es oszcillátort, amely nagyfrekvenciás zajt visz be a hangjelbe.
Az oszcilloszkópon látható jel továbbra is csak egy feszültségsorozat lesz, az idő minden pillanatában egy értékkel, de a jel másképp fog kinézni, mert az időtartománybeli változásainak most már az 5 kHz-es szinuszhullámot és a nagyfrekvenciás zaj ingadozását is tükröznie kell.
A frekvenciatartományban azonban a szinusz és a zaj külön frekvenciakomponensek, amelyek egyszerre vannak jelen ebben az egy jelben. A szinuszhullám és a zaj a jel frekvenciatartománybeli ábrázolásának különböző részeit foglalja el (ahogy az alábbi ábrán látható), és ez azt jelenti, hogy a zajt úgy tudjuk kiszűrni, hogy a jelet olyan áramkörön keresztül vezetjük, amely az alacsony frekvenciákat átengedi, a magas frekvenciákat pedig blokkolja.
A szűrők típusai
A szűrőket nagyjából olyan kategóriákba lehet sorolni, amelyek megfelelnek a szűrő frekvenciaválaszának általános jellemzőinek. Ha egy szűrő alacsony frekvenciákat enged át és magas frekvenciákat blokkol, akkor aluláteresztő szűrőnek nevezzük. Ha az alacsony frekvenciákat blokkolja, a magas frekvenciákat pedig átengedi, akkor magaspassszűrőnek nevezzük. Vannak továbbá sáteresztő szűrők, amelyek csak egy viszonylag szűk frekvenciatartományt engednek át, és sávszűrők, amelyek csak egy viszonylag szűk frekvenciatartományt blokkolnak.

A szűrőket az áramkör megvalósításához használt alkatrészek típusa szerint is osztályozhatjuk. A passzív szűrők ellenállásokat, kondenzátorokat és induktivitásokat használnak; ezek az alkatrészek nem képesek erősítésre, következésképpen egy passzív szűrő csak a bemeneti jel amplitúdóját képes fenntartani vagy csökkenteni. Az aktív szűrő ezzel szemben egyszerre képes szűrni a jelet és erősítést alkalmazni, mivel aktív alkatrészt, például tranzisztort vagy műveleti erősítőt tartalmaz.

Ez az aktív aluláteresztő szűrő a népszerű Sallen-Key topológián alapul.
Ez a cikk a passzív aluláteresztő szűrők elemzését és tervezését vizsgálja. Ezek az áramkörök fontos szerepet játszanak a legkülönbözőbb rendszerekben és alkalmazásokban.
Az RC aluláteresztő szűrő
A passzív aluláteresztő szűrő létrehozásához egy ellenállásos elemet kell kombinálnunk egy reaktív elemmel. Más szóval olyan áramkörre van szükségünk, amely egy ellenállásból és egy kondenzátorból vagy egy induktorból áll. Elméletileg az ellenállás-induktor (RL) aluláteresztő topológia a szűrési képesség szempontjából egyenértékű az ellenállás-kondenzátor (RC) aluláteresztő topológiával. A gyakorlatban azonban az ellenállás-kondenzátor változat sokkal gyakoribb, ezért a cikk további részében az RC aluláteresztő szűrőre fogunk koncentrálni.
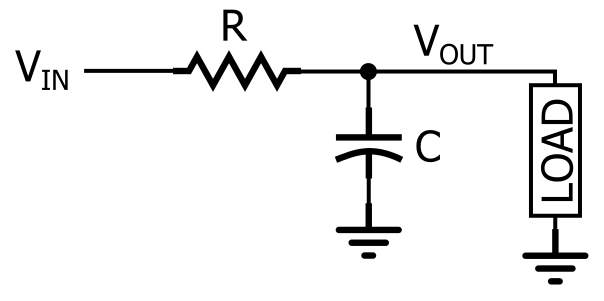
Az RC aluláteresztő szűrő.
Amint az ábrán látható, az RC aluláteresztő válasz úgy jön létre, hogy egy ellenállást sorba kapcsolunk a jelútvonallal, és egy kondenzátort párhuzamosan a terheléssel. Az ábrán a terhelés egyetlen komponens, de egy valós áramkörben ez lehet valami sokkal bonyolultabb, például egy analóg-digitális átalakító, egy erősítő vagy a szűrő válaszának mérésére használt oszcilloszkóp bemeneti fokozata.
Az RC aluláteresztő topológia szűrőhatását intuitív módon elemezhetjük, ha felismerjük, hogy az ellenállás és a kondenzátor egy frekvenciafüggő feszültségosztót alkot.

Az RC aluláteresztő szűrő átrajzolva, hogy úgy nézzen ki, mint egy feszültségosztó.
Amikor a bemeneti jel frekvenciája alacsony, a kondenzátor impedanciája magas az ellenállás impedanciájához képest; így a bemeneti feszültség nagy része a kondenzátoron (és a kondenzátorral párhuzamos terhelésen) esik le. Ha a bemeneti frekvencia magas, a kondenzátor impedanciája alacsony az ellenállás impedanciájához képest, ami azt jelenti, hogy több feszültség esik le az ellenálláson, és kevesebb kerül át a terhelésre. Így az alacsony frekvenciák átjutnak, a magas frekvenciák pedig blokkolva vannak.
Az RC aluláteresztő funkciójának ez a minőségi magyarázata fontos első lépés, de nem túl hasznos, amikor ténylegesen meg kell terveznünk egy áramkört, mivel a “magas frekvencia” és az “alacsony frekvencia” kifejezések rendkívül homályosak. A mérnököknek olyan áramköröket kell létrehozniuk, amelyek meghatározott frekvenciákat engednek át és blokkolnak. Például a fent leírt audiorendszerben egy 5 kHz-es jelet szeretnénk megőrizni, és egy 500 kHz-es jelet elnyomni. Ez azt jelenti, hogy olyan szűrőre van szükségünk, amely valahol 5 kHz és 500 kHz között vált át az átbocsátásból a blokkolásba.
A határfrekvencia
Azoknak a frekvenciáknak a tartományát, amelyeknél a szűrő nem okoz jelentős csillapítást, átbocsátási sávnak nevezzük, és azoknak a frekvenciáknak a tartományát, amelyeknél a szűrő jelentős csillapítást okoz, tiltási sávnak nevezzük. Az analóg szűrők, például az RC aluláteresztő szűrő, mindig fokozatosan lépnek át az áteresztő sávból a záró sávba. Ez azt jelenti, hogy nem lehet meghatározni egyetlen olyan frekvenciát, amelynél a szűrő már nem engedi át a jeleket, és elkezdi blokkolni a jeleket. A mérnököknek azonban szükségük van arra, hogy egy szűrő frekvenciaválaszát kényelmesen és tömören összefoglalják, és itt jön a képbe a határfrekvencia fogalma.
Ha megnézzük egy RC-szűrő frekvenciaválaszának ábráját, észrevehetjük, hogy a “határfrekvencia” kifejezés nem túl pontos. Az a kép, hogy a jel spektrumát két részre “vágják”, amelyek közül az egyiket megtartják, a másikat pedig elvetik, nem alkalmazható, mivel a csillapítás fokozatosan növekszik, ahogy a frekvenciák a határérték alattról a határérték fölé haladnak.
Az RC aluláteresztő szűrő határfrekvenciája valójában az a frekvencia, amelynél a bemeneti jel amplitúdója 3 dB-lel csökken (ezt az értéket azért választottuk, mert az amplitúdó 3 dB-es csökkenése 50%-os teljesítménycsökkenésnek felel meg). Ezért a határfrekvenciát -3 dB-es frekvenciának is nevezik, és valójában ez az elnevezés pontosabb és informatívabb. A sávszélesség kifejezés a szűrő átviteli sávjának szélességére utal, és egy aluláteresztő szűrő esetében a sávszélesség megegyezik a -3 dB frekvenciával (ahogy az alábbi diagramon látható).

Ez a diagram egy RC aluláteresztő szűrő frekvenciaválaszának általános jellemzőit közvetíti. A sávszélesség megegyezik a -3 dB frekvenciával.
A fentiek szerint az RC-szűrő aluláteresztő viselkedését az ellenállás frekvenciafüggetlen impedanciája és a kondenzátor frekvenciafüggő impedanciája közötti kölcsönhatás okozza. Ahhoz, hogy meghatározzuk a szűrő frekvenciaválaszának részleteit, matematikailag elemeznünk kell az ellenállás (R) és a kapacitás (C) közötti kapcsolatot, és ezeket az értékeket manipulálni is tudjuk, hogy olyan szűrőt tervezzünk, amely megfelel a pontos specifikációknak. Egy RC aluláteresztő szűrő határfrekvenciáját (fC) a következőképpen számíthatjuk ki:
Nézzünk egy egyszerű tervezési példát. A kondenzátorértékek korlátozottabbak, mint az ellenállásértékek, ezért egy általános kapacitásértékkel kezdünk (például 10 nF), majd az egyenlet segítségével meghatározzuk a szükséges ellenállásértéket. A cél egy olyan szűrő tervezése, amely megőrzi az 5 kHz-es hanghullámformát, és elutasít egy 500 kHz-es zajhullámformát. Kipróbálunk egy 100 kHz-es határfrekvenciát, és a cikk későbbi részében alaposabban elemezzük a szűrő hatását a két frekvenciakomponensre.

Egy 160 Ω ellenállás és egy 10 nF kondenzátor kombinációjával tehát olyan szűrőt kapunk, amely nagyjából megközelíti a kívánt frekvenciaválaszt.
A szűrő válaszának kiszámítása
Az aluláteresztő szűrő elméleti viselkedését egy tipikus feszültségosztó számítás frekvenciafüggő változatával tudjuk kiszámítani. Egy ellenállásos feszültségosztó kimenete a következőképpen fejezhető ki:


Az RC-szűrő ezzel egyenértékű szerkezetet használ, de R2 helyett egy kondenzátort kapunk. Először is, az R2-t (a számlálóban) helyettesítjük a kondenzátor reaktanciájával (XC). Ezután ki kell számolnunk a teljes impedancia nagyságát, és ezt helyezzük a nevezőbe. Így megkapjuk

A kondenzátor reaktanciája az áramáramlással szembeni ellenállás mértékét jelzi, de az ellenállás mértékét az ellenállással ellentétben a kondenzátoron áthaladó jel frekvenciája határozza meg. Ezért a reaktanciát egy adott frekvencián kell kiszámítanunk, és az ehhez használt egyenlet a következő:

A fenti tervezési példában R ≈ 160 Ω és C = 10 nF. Feltételezzük, hogy a VIN amplitúdója 1 V, így a VIN-t egyszerűen kivehetjük a számításból. Először is számítsuk ki a VOUT amplitúdóját a szinuszhullám frekvenciáján:


A szinuszhullám amplitúdója lényegében nem változik. Ez jó, hiszen az volt a célunk, hogy a zaj elnyomása mellett megőrizzük a szinuszhullámot. Ez az eredmény nem meglepő, hiszen olyan határfrekvenciát (100 kHz) választottunk, amely jóval magasabb, mint a szinuszhullám frekvenciája (5 kHz).
Most nézzük meg, hogy a szűrő milyen sikeresen csillapítja a zajkomponenst.

A zaj amplitúdója az eredeti értéknek csak körülbelül 20%-a.
A szűrő válaszának szemléltetése
A szűrő jelre gyakorolt hatásának értékeléséhez a legkényelmesebb eszköz a szűrő frekvenciaválaszának ábrázolása. Ezek a gyakran Bode-diagramnak nevezett grafikonok a függőleges tengelyen a nagyságot (decibelben), a vízszintes tengelyen pedig a frekvenciát ábrázolják; a vízszintes tengely általában logaritmikus skálával rendelkezik, úgy, hogy az 1 Hz és 10 Hz közötti fizikai távolság megegyezik a 10 Hz és 100 Hz, a 100 Hz és 1 kHz közötti fizikai távolsággal, és így tovább. Ez a konfiguráció lehetővé teszi egy szűrő viselkedésének gyors és pontos értékelését nagyon nagy frekvenciatartományban.

Egy példa a frekvencia-válasz diagramra.
A görbe minden egyes pontja azt a nagyságot jelzi, amellyel a kimeneti jel rendelkezik, ha a bemeneti jel nagysága 1 V, frekvenciája pedig megegyezik a vízszintes tengely megfelelő értékével. Például, ha a bemeneti frekvencia 1 MHz, a kimeneti amplitúdó (1 V bemeneti amplitúdót feltételezve) 0,1 V lesz (mivel -20 dB tízszeres csökkenésnek felel meg).
A frekvencia-válaszgörbe általános alakja nagyon ismerős lesz, ha több időt töltesz a szűrőáramkörökkel. A görbe az átviteli sávban szinte tökéletesen lapos, majd a bemeneti frekvencia közeledésével a határfrekvenciához egyre gyorsabban kezd csökkenni. Végül a csillapítás változásának mértéke, amelyet roll-offnak nevezünk, 20 dB/dekádnál stabilizálódik – azaz a kimeneti jel nagysága 20 dB-lel csökken a bemeneti frekvencia minden egyes tízszeres növekedésére.
Az aluláteresztő szűrő teljesítményének értékelése
Ha a cikkben korábban megtervezett szűrő frekvenciaválaszát gondosan ábrázoljuk, akkor láthatjuk, hogy a nagyságfüggvény 5 kHz-en lényegében 0 dB (azaz, szinte nulla csillapítás), az 500 kHz-en mért nagyságrendi válasz pedig körülbelül -14 dB (ami 0,2-es erősítésnek felel meg). Ezek az értékek összhangban vannak az előző részben elvégzett számítások eredményeivel.
Mivel az RC-szűrők mindig fokozatos átmenettel rendelkeznek az áteresztő sávtól a záró sávig, és mivel a csillapítás soha nem éri el a végtelent, nem tervezhetünk “tökéletes” szűrőt – azaz olyan szűrőt, amely nincs hatással a szinuszhullámra, és teljesen kiküszöböli a zajt. Ehelyett mindig kompromisszumot kell kötnünk. Ha a határfrekvenciát közelebb visszük az 5 kHz-hez, akkor nagyobb lesz a zajcsillapítás, de a hangszóróra küldendő szinuszhullám csillapítása is nagyobb lesz. Ha a határfrekvenciát közelebb visszük 500 kHz-hez, akkor kevesebb csillapításunk lesz a szinuszhullám frekvenciáján, de kevesebb csillapításunk lesz a zajfrekvencián is.
Az aluláteresztő szűrő fáziseltolódása
Az eddigiekben azt tárgyaltuk, hogyan módosítja egy szűrő a jel különböző frekvenciakomponenseinek amplitúdóját. A reaktív áramköri elemek azonban az amplitúdóhatások mellett mindig fáziseltolódást is okoznak.
A fázis fogalma egy periodikus jel értékére utal egy cikluson belül egy adott pillanatban. Amikor tehát azt mondjuk, hogy egy áramkör fáziseltolódást okoz, úgy értjük, hogy a bemeneti jel és a kimeneti jel között eltolódást hoz létre: a bemeneti és a kimeneti jelek már nem ugyanabban az időpontban kezdik és fejezik be a ciklusukat. A fáziseltolódás értéke, például 45° vagy 90°, azt jelzi, hogy mekkora eltolódás jött létre.
Az áramkör minden reaktív eleme 90°-os fáziseltolódást hoz létre, de ez a fáziseltolódás nem egyszerre történik. A kimeneti jel fázisa, csakúgy, mint a kimeneti jel nagysága, fokozatosan változik a bemeneti frekvencia növekedésével. Egy RC aluláteresztő szűrőben egy reaktív elemünk van (a kondenzátor), és következésképpen az áramkör végül 90°-os fáziseltolódást fog bevezetni.
Amint a nagyságrendi válasz esetében, a fázisválasz is legegyszerűbben egy olyan diagram vizsgálatával értékelhető, amelynek vízszintes tengelye a logaritmikus frekvenciát jelzi. Az alábbi leírás az általános mintát közvetíti, majd a grafikon vizsgálatával kitöltheti a részleteket.
- A fáziseltolódás kezdetben 0°.
- A fáziseltolódás fokozatosan növekszik, amíg el nem éri a 45°-ot a határfrekvencián; a válasz ezen szakasza alatt a változás mértéke növekszik.
- A határfrekvencia után a fáziseltolódás tovább növekszik, de a változás sebessége csökken.
- A változás sebessége nagyon kicsi lesz, ahogy a fáziseltolódás aszimptotikusan megközelíti a 90°-ot.

A folytonos vonal a nagyságválasz, a szaggatott vonal pedig a fázisválasz. A határfrekvencia 100 kHz. Vegyük észre, hogy a fáziseltolódás 45° a határfrekvencián.
Másodrendű aluláteresztő szűrők
Az eddigiekben feltételeztük, hogy egy RC aluláteresztő szűrő egy ellenállásból és egy kondenzátorból áll. Ez a konfiguráció egy elsőrendű szűrő.
A passzív szűrő “rendjét” az áramkörben jelen lévő reaktív elemek – azaz kondenzátorok vagy induktorok – száma határozza meg. Egy magasabb rendű szűrő több reaktív elemmel rendelkezik, és ez nagyobb fáziseltolódást és meredekebb lecsengést eredményez. Ez a második jellemző az elsődleges motiváció a szűrő rendjének növelésére.
Egy reaktív elem hozzáadásával a szűrőhöz – például az elsőrendűről a másodrendűre vagy a másodrendűről a harmadrendűre való áttéréssel – 20 dB/dekáddal növeljük a maximális roll-offot. A meredekebb roll-off gyorsabb átmenetet jelent az alacsony csillapításról a magas csillapításra, és ez jobb teljesítményt eredményezhet, ha a jelnek nincs olyan széles frekvenciasávja, amely elválasztja a kívánt frekvenciakomponenseket a zajkomponensektől.
A másodrendű szűrőket általában egy induktorból és egy kondenzátorból álló rezonáns áramkör köré építik (ezt a topológiát “RLC”-nek nevezik, ami ellenállás-induktor-kondenzátor). Lehetőség van azonban másodrendű RC-szűrők létrehozására is. Ahogy az alábbi ábrán látható, mindössze két elsőrendű RC-szűrőt kell kaszkádba kapcsolnunk.

Bár ez a topológia kétségtelenül létrehoz egy másodrendű választ, nem használják széles körben – ahogy a következő szakaszban látni fogjuk, a frekvenciaválasz gyakran rosszabb, mint egy másodrendű aktív szűrőé vagy egy másodrendű RLC-szűrőé.
A másodrendű RC-szűrő frekvenciaválasza
A másodrendű RC aluláteresztő szűrő létrehozására úgy tehetünk kísérletet, hogy a kívánt határfrekvenciának megfelelően megtervezünk egy elsőrendű szűrőt, majd két ilyen elsőrendű fokozatot sorba kapcsolunk. Ez valóban egy olyan szűrőt eredményez, amelynek teljes frekvenciaválasza hasonló, és a maximális roll-off értéke 20 dB/dekád helyett 40 dB/dekád.
Ha azonban közelebbről megvizsgáljuk a választ, azt látjuk, hogy a -3 dB frekvencia csökkent. A másodrendű RC-szűrő nem a várt módon viselkedik, mivel a két fokozat nem független – nem tudjuk egyszerűen összekapcsolni a két fokozatot, és az áramkört úgy elemezni, mint egy elsőrendű aluláteresztő szűrőt, amelyet egy azonos elsőrendű aluláteresztő szűrő követ.
Még akkor is, ha a két fokozat közé puffert illesztünk, hogy az első és a második RC fokozat független szűrőként működhessen, a csillapítás az eredeti határfrekvencián 3 dB helyett 6 dB lesz. Ez pontosan azért következik be, mert a két fokozat egymástól függetlenül működik – az első szűrő 3 dB csillapítással rendelkezik a határfrekvencián, a második szűrő pedig további 3 dB csillapítást ad hozzá.

A másodrendű RC aluláteresztő szűrő alapvető korlátja, hogy a tervező nem tudja finomhangolni az átmenetet az áteresztől a zártsávig a szűrő Q-tényezőjének beállításával; ez a paraméter azt mutatja, hogy a frekvenciaválasz mennyire csillapított. Ha két azonos RC aluláteresztő szűrőt kaszkádba kapcsol, a teljes átviteli függvény megfelel egy másodrendű válasznak, de a Q-tényező mindig 0,5 lesz. Ha Q = 0,5, a szűrő a túltompítás határán van, és ez olyan frekvenciaválaszt eredményez, amely az átmeneti tartományban “megereszkedik”. A másodrendű aktív szűrők és a másodrendű rezonancia alapú szűrők nem rendelkeznek ezzel a korlátozással; a tervező szabályozhatja a Q tényezőt, és ezáltal finomhangolhatja a frekvenciaválaszt az átmeneti tartományban.
Összefoglaló
- Minden elektromos jel a kívánt és a nem kívánt frekvenciakomponensek keverékét tartalmazza. A nemkívánatos frekvenciakomponenseket jellemzően a zaj és az interferencia okozza, és bizonyos helyzetekben negatívan befolyásolják a rendszer teljesítményét.
- A szűrő olyan áramkör, amely különböző módon reagál a jel spektrumának különböző részeire. Az aluláteresztő szűrőt úgy tervezték, hogy átengedje az alacsony frekvenciájú komponenseket, és blokkolja a magas frekvenciájú komponenseket.
- Az aluláteresztő szűrő határfrekvenciája azt a frekvenciatartományt jelzi, amelyben a szűrő az alacsony csillapításból jelentős csillapításba megy át.
- Az RC aluláteresztő szűrő kimeneti feszültségét úgy lehet kiszámítani, hogy az áramkört egy (frekvenciafüggetlen) ellenállásból és egy (frekvenciafüggő) reaktanciából álló feszültségosztóként kezeljük.
- A nagyság (dB-ben, a függőleges tengelyen) és a logaritmikus frekvencia (hertz-ben, a vízszintes tengelyen) grafikonja kényelmes és hatékony módja a szűrő elméleti viselkedésének vizsgálatára. A fázis és a logaritmikus frekvencia közötti ábrát is használhatja a bemeneti jelre alkalmazott fáziseltolás mértékének meghatározásához.
- A másodrendű szűrő meredekebb roll-off-ot biztosít; ez a másodrendű válasz akkor hasznos, ha egy jel nem biztosít széles sávot a kívánt frekvenciakomponensek és a nemkívánatos frekvenciakomponensek elkülönítésére.
- Egy másodrendű RC aluláteresztő szűrőt úgy hozhat létre, hogy két azonos elsőrendű RC aluláteresztő szűrőt épít, majd az egyik kimenetét a másik bemenetéhez kapcsolja. A teljes -3 dB frekvencia a vártnál alacsonyabb lesz.