Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. Bármelyik ábrát megnézheted – mindkettő megragadja a legfontosabb információkat: mely földdarabok milyen más földdarabokkal vannak összekötve, és hány híddal.
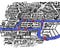
A technikai nyelven ezt grafikonként ábrázoljuk. A földdarabok a csúcsok, a hidak pedig az élek. De ez nem fontos.
A probléma az, hogy lehetséges-e olyan útvonalat találni, amely minden hídon pontosan egyszer megy át. Ez azt jelenti, hogy a városban tett sétánk során azt akarjuk, hogy az útvonalunk minden hídon átmenjen, de nem mehet át kétszer, vagy háromszor… Alapvetően, ha ugyanazon a hídon találjuk magunkat, mint korábban, akkor az útvonal érvénytelen. Ha befejezed a sétádat, és van egy híd, amin nem mentél át, akkor az útvonalad érvénytelen volt.
A megoldás
Nézz meg minden egyes földdarabot. Minden híd két földdarabhoz kapcsolódik (így működnek a hidak). Minden egyes földdarabhoz történetesen páratlan számú híd kapcsolódik.
Most nézzük meg, hogyan nézne ki egy érvényes séta.
Amíg sétálsz, egy jegyzettömbbe minden egyes alkalommal feljegyzed, amikor egy adott földdarabon jársz. Ha például a város legdélebbi végében indulsz el, akkor azt feljegyzed (fényképet készítesz, szuvenírt veszel…), és ha újra ott találod magad, akkor kettőre növeled a déli szektorra vonatkozó számlát.
Minden egyes földdarab esetében két eset van
(1) ez egy olyan városrész, ahol nem kezdjük a sétánkat, és nem is fejezzük be ott a sétánkat
(2) ez egy olyan városrész, ahol vagy elkezdjük a sétánkat, vagy befejezzük a sétánkat, vagy mindkettő.
Látható, hogy a második típusú városrészből legfeljebb 2 van. Nem kezdhetünk egyszerre két helyen, és nem is fejezhetjük be egyszerre két helyen.
Mivel a városnak négy szakasza van, ez azt jelenti, hogy a sétánk során legalább két olyan szakasza van a városnak, amelyben nem fejezzük be, és nem is kezdjük el. Válasszunk ki egyet közülük.
Amikor bemegyünk abba a szektorba, akkor egy hidat használunk fel, és amikor elhagyjuk, akkor egy másikat. De, minden szektorhoz páratlan számú híd tartozik! Ez ellentmondás. Hogy lássuk, miért, emlékezzünk vissza, hogy minden szektorhoz vagy 3 híd tartozik, vagy 5 híd van hozzácsatolva.
Ha egyszer vagyunk a szektorban, akkor csak két hidat használhatunk fel a szektor hídjai közül. Ha kétszer vagyunk benne, akkor négy hídját használjuk el (vagy elfogynak a hidak, ha csak három hídja lenne). Ha háromszor vagyunk benne, akkor 6 hídra lenne szükségünk, ami nem áll rendelkezésünkre. Tehát az a követelmény, hogy a városnak egy olyan szektorába lépjünk be és egy olyan szektorát hagyjuk el, amely nem a kezdő- vagy végpontunk, ellentmond annak a ténynek, hogy az összekötő hidak száma minden szektorban páratlan.