Lunghezza d’onda
In mezzi lineari, qualsiasi modello d’onda può essere descritto in termini di propagazione indipendente di componenti sinusoidali. La lunghezza d’onda λ di una forma d’onda sinusoidale che viaggia a velocità costante v è data da
λ = v f , {displaystyle \lambda ={frac {v}{f}},\,

dove v è chiamata la velocità di fase (grandezza della velocità di fase) dell’onda e f è la frequenza dell’onda. In un mezzo dispersivo, la velocità di fase stessa dipende dalla frequenza dell’onda, rendendo la relazione tra lunghezza d’onda e frequenza non lineare.
Nel caso della radiazione elettromagnetica – come la luce – nello spazio libero, la velocità di fase è la velocità della luce, circa 3×108 m/s. Così la lunghezza d’onda di un’onda elettromagnetica (radio) di 100 MHz è circa: 3×108 m/s diviso 108 Hz = 3 metri. La lunghezza d’onda della luce visibile va dal rosso intenso, circa 700 nm, al violetto, circa 400 nm (per altri esempi, vedi spettro elettromagnetico).
Per le onde sonore nell’aria, la velocità del suono è 343 m/s (a temperatura ambiente e pressione atmosferica). Le lunghezze d’onda delle frequenze sonore udibili dall’orecchio umano (20 Hz-20 kHz) sono quindi tra circa 17 m e 17 mm, rispettivamente. Frequenze un po’ più alte sono utilizzate dai pipistrelli in modo da poter risolvere obiettivi più piccoli di 17 mm. Le lunghezze d’onda del suono udibile sono molto più lunghe di quelle della luce visibile.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Per esempio, per un’onda elettromagnetica, se la scatola ha pareti metalliche ideali, la condizione per i nodi alle pareti risulta perché le pareti metalliche non possono sostenere un campo elettrico tangenziale, costringendo l’onda ad avere ampiezza zero alla parete.
L’onda stazionaria può essere vista come la somma di due onde sinusoidali viaggianti di velocità opposte. Di conseguenza, la lunghezza d’onda, il periodo e la velocità dell’onda sono correlati proprio come per un’onda viaggiante. Per esempio, la velocità della luce può essere determinata dall’osservazione delle onde stazionarie in una scatola di metallo contenente un vuoto ideale.
Rappresentazione matematicaModifica
Le onde sinusoidali viaggianti sono spesso rappresentate matematicamente in termini della loro velocità v (nella direzione x), frequenza f e lunghezza d’onda λ come:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ) {\displaystyle y(x,\t)=A\cos \sinistra(2\pi \sinistra({frac {x}{lambda}-ft\destra)\destra)=A\cos \sinistra({frac {2\pi \lambda}(x-vt)\destra)}

dove y è il valore dell’onda in qualsiasi posizione x e tempo t, e A è l’ampiezza dell’onda. Sono anche comunemente espressi in termini di numero d’onda k (2π volte il reciproco della lunghezza d’onda) e frequenza angolare ω (2π volte la frequenza) come:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\displaystyle y(x,\t)=A\cos \sinistra(kx-\omega t\destra)=A\cos \sinistra(k(x-vt)\destra)}

in cui lunghezza d’onda e numero d’onda sono correlati alla velocità e alla frequenza come:
k = 2 π λ = 2 π f v = ω v , {displaystyle k={frac {2\pi }{lambda }}={frac {2\pi f}{v}={frac {\omega }{v}},

o
λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={frac {2\pi }{k}={frac {2\pi v}{\omega }={frac {v}{frac {v}{f}.

Nella seconda forma data sopra, la fase (kx – ωt) è spesso generalizzata a (k-r – ωt), sostituendo il numero d’onda k con un vettore d’onda che specifica la direzione e il numero d’onda di un’onda piana nello spazio 3, parametrizzata dal vettore posizione r. In questo caso, il numero d’onda k, la grandezza di k, è ancora nella stessa relazione con la lunghezza d’onda come mostrato sopra, con v interpretato come velocità scalare nella direzione del vettore d’onda. La prima forma, usando la lunghezza d’onda reciproca nella fase, non si generalizza così facilmente a un’onda in una direzione arbitraria.
Generalizzazioni a sinusoidi di altre fasi, e a esponenziali complessi, sono anche comuni; vedi onda piana. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. In particolare, la velocità della luce in un mezzo è minore che nel vuoto, il che significa che la stessa frequenza corrisponderà a una lunghezza d’onda più corta nel mezzo che nel vuoto, come mostrato nella figura a destra.
Questo cambiamento di velocità quando entra in un mezzo causa la rifrazione, o un cambiamento di direzione delle onde che incontrano l’interfaccia tra i mezzi con un angolo. Per le onde elettromagnetiche, questo cambiamento nell’angolo di propagazione è governato dalla legge di Snell.
La velocità dell’onda in un mezzo non solo può differire da quella in un altro, ma la velocità varia tipicamente con la lunghezza d’onda. Di conseguenza, il cambiamento di direzione quando entra in un mezzo diverso cambia con la lunghezza d’onda dell’onda.
Per le onde elettromagnetiche la velocità in un mezzo è governata dal suo indice di rifrazione secondo
v = c n ( λ 0 ) , {displaystyle v={frac {c}{n(\lambda _{0})},}

dove c è la velocità della luce nel vuoto e n(λ0) è l’indice di rifrazione del mezzo alla lunghezza d’onda λ0, dove quest’ultima è misurata nel vuoto piuttosto che nel mezzo. La lunghezza d’onda corrispondente nel mezzo è
λ = λ 0 n ( λ 0 ) . {displaystyle \lambda ={frac {lambda _{0}}{n(\lambda _{0})}}.}

Quando si citano le lunghezze d’onda della radiazione elettromagnetica, di solito si intende la lunghezza d’onda nel vuoto a meno che la lunghezza d’onda non sia specificatamente identificata come la lunghezza d’onda in qualche altro mezzo. In acustica, dove un mezzo è essenziale per l’esistenza delle onde, il valore della lunghezza d’onda è dato per un mezzo specificato.
La variazione della velocità della luce con la lunghezza d’onda è nota come dispersione, ed è anche responsabile del fenomeno familiare in cui la luce è separata in colori componenti da un prisma. La separazione avviene quando l’indice di rifrazione all’interno del prisma varia con la lunghezza d’onda, quindi lunghezze d’onda diverse si propagano a velocità diverse all’interno del prisma, facendole rifrangere ad angoli diversi. La relazione matematica che descrive come la velocità della luce all’interno di un mezzo varia con la lunghezza d’onda è nota come relazione di dispersione.
MediaEdit non uniformi

La lunghezza d’onda può essere un concetto utile anche se l’onda non è periodica nello spazio. Per esempio, in un’onda oceanica che si avvicina alla riva, mostrata in figura, l’onda in arrivo ondeggia con una lunghezza d’onda locale variabile che dipende in parte dalla profondità del fondo del mare rispetto all’altezza dell’onda. L’analisi dell’onda può essere basata sul confronto della lunghezza d’onda locale con la profondità dell’acqua locale.

Le onde che sono sinusoidali nel tempo ma si propagano attraverso un mezzo le cui proprietà variano con la posizione (un mezzo non omogeneo) possono propagarsi ad una velocità che varia con la posizione, e di conseguenza possono non essere sinusoidali nello spazio. La figura a destra mostra un esempio. Come l’onda rallenta, la lunghezza d’onda diventa più corta e l’ampiezza aumenta; dopo un luogo di massima risposta, la lunghezza d’onda corta è associata ad un’alta perdita e l’onda si spegne.
L’analisi delle equazioni differenziali di tali sistemi è spesso fatta approssimativamente, usando il metodo WKB (noto anche come metodo Liouville-Green). Il metodo integra la fase attraverso lo spazio usando un numero d’onda locale, che può essere interpretato come indicante una “lunghezza d’onda locale” della soluzione in funzione del tempo e dello spazio.Questo metodo tratta il sistema localmente come se fosse uniforme con le proprietà locali; in particolare, la velocità d’onda locale associata a una frequenza è l’unica cosa necessaria per stimare il corrispondente numero d’onda locale o lunghezza d’onda. Inoltre, il metodo calcola un’ampiezza che cambia lentamente per soddisfare altri vincoli delle equazioni o del sistema fisico, come per la conservazione dell’energia nell’onda.
CrystalsEdit
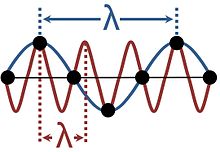
Le onde nei solidi cristallini non sono continue, perché sono composte da vibrazioni di particelle discrete disposte in un reticolo regolare. Questo produce aliasing perché la stessa vibrazione può essere considerata come avente una varietà di lunghezze d’onda diverse, come mostrato in figura. Le descrizioni che utilizzano più di una di queste lunghezze d’onda sono ridondanti; è convenzionale scegliere la lunghezza d’onda più lunga che si adatta al fenomeno. La gamma di lunghezze d’onda sufficienti a fornire una descrizione di tutte le possibili onde in un mezzo cristallino corrisponde ai vettori d’onda confinati nella zona di Brillouin.
Questa indeterminazione della lunghezza d’onda nei solidi è importante nell’analisi dei fenomeni ondulatori come le bande di energia e le vibrazioni del reticolo. È matematicamente equivalente all’aliasing di un segnale campionato a intervalli discreti.