10.13: Hipoteza Avogadro’a i objętość molowa
Objętość Avogadro’a i objętość molowa
Objętość jest trzecim sposobem mierzenia ilości materii, po liczbie sztuk i masie. W przypadku cieczy i ciał stałych, objętość różni się znacznie w zależności od gęstości substancji. Dzieje się tak dlatego, że cząsteczki ciał stałych i cieczy są upakowane blisko siebie z bardzo małą przestrzenią pomiędzy cząsteczkami. Jednak gazy składają się w dużej mierze z pustych przestrzeni pomiędzy cząsteczkami gazu (patrz rysunek poniżej).
W 1811 roku Amadeo Avogadro wyjaśnił, że objętości wszystkich gazów można łatwo wyznaczyć. Hipoteza Avogadro mówi, że jednakowe objętości wszystkich gazów w tej samej temperaturze i pod tym samym ciśnieniem zawierają jednakową liczbę cząsteczek. Ponieważ całkowita objętość gazu składa się głównie z pustej przestrzeni pomiędzy cząsteczkami, rzeczywiste rozmiary cząsteczek są prawie nieistotne. Dana objętość gazu o małych, lekkich cząsteczkach, takiego jak wodór, zawiera taką samą liczbę cząsteczek, jak ta sama objętość ciężkiego gazu o dużych cząsteczkach, takiego jak sześciofluorek siarki,
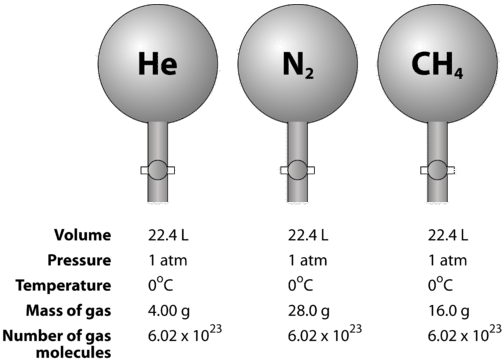
Gazy są ściśliwe, co oznacza, że po poddaniu ich wysokiemu ciśnieniu cząsteczki zbliżają się do siebie. Zmniejsza to ilość pustej przestrzeni i zmniejsza objętość gazu. Na objętość gazu ma również wpływ temperatura. Kiedy gaz jest podgrzewany, jego cząsteczki poruszają się szybciej i gaz się rozszerza. Z powodu zmian objętości gazu spowodowanych zmianami ciśnienia i temperatury, porównanie objętości gazu musi być dokonywane w jednej standardowej temperaturze i ciśnieniu. Objętość molowa gazu to objętość jednego mola gazu w temperaturze STP. W temperaturze STP jeden mol (6,02 razy 10^{23}} cząsteczek reprezentatywnych) dowolnego gazu zajmuje objętość \(22,4 \: \text{L}) (rysunek poniżej).

Poniższy rysunek ilustruje, jak objętość molowa może być postrzegana przy porównywaniu różnych gazów. Próbki helu (po lewej stronie), azotu (po prawej stronie) i metanu (po lewej stronie) znajdują się w temperaturze STP. Każdy z nich zawiera 1 mol, czyli 6,02 razy 10^{23}} cząsteczek. Jednak masa każdego gazu jest inna i odpowiada masie molowej tego gazu: \(4,00 \\) dla \He}, \(28,0 \) dla \N_2} i \(16,0 \) dla \CH_4}.