Co to jest filtr dolnoprzepustowy? A Tutorial on the Basics of Passive RC Filters

Co to jest filtrowanie? Dowiedz się, czym są filtry dolnoprzepustowe rezystor-kondensator (RC) i gdzie można je stosować.

W tym artykule wprowadzono pojęcie filtrowania i szczegółowo wyjaśniono cel i charakterystykę filtrów dolnoprzepustowych rezystor-kondensator (RC).

Domena czasu i domena częstotliwości

Gdy patrzysz na sygnał elektryczny na oscyloskopie, widzisz linię, która reprezentuje zmiany napięcia w odniesieniu do czasu. W każdym konkretnym momencie czasowym sygnał ma tylko jedną wartość napięcia. To co widzisz na oscyloskopie jest reprezentacją sygnału w dziedzinie czasu.

Typowy ślad oscyloskopu jest prosty i intuicyjny, ale jest również nieco ograniczający, ponieważ nie ujawnia bezpośrednio zawartości częstotliwościowej sygnału. W przeciwieństwie do reprezentacji w dziedzinie czasu, w której jeden moment w czasie odpowiada tylko jednej wartości napięcia, reprezentacja w dziedzinie częstotliwości (zwana również widmem) przekazuje informacje o sygnale poprzez identyfikację różnych składowych częstotliwości, które są jednocześnie obecne.

Przedstawienia w dziedzinie czasu sinusoidy (góra) i fali kwadratowej (dół).

Przedstawienia sinusoidy (góra) i fali kwadratowej (dół) w dziedzinie częstotliwości.

Co to jest filtr?

Filtr jest obwodem, który usuwa, lub „odfiltrowuje”, określony zakres składowych częstotliwości. Innymi słowy, rozdziela widmo sygnału na składowe częstotliwości, które będą przepuszczane i składowe częstotliwości, które będą blokowane.

Jeśli nie masz dużego doświadczenia z analizą w dziedzinie częstotliwości, możesz nadal nie być pewien czym są te składowe częstotliwości i jak współistnieją w sygnale, który nie może mieć wielu wartości napięcia w tym samym czasie. Przyjrzyjmy się krótkiemu przykładowi, który pomoże wyjaśnić tę koncepcję.

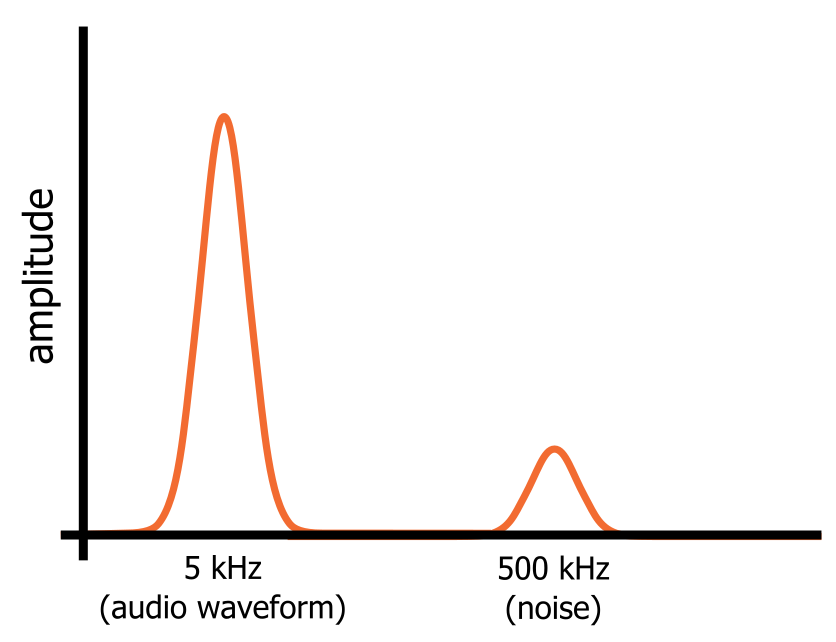
Wyobraźmy sobie, że mamy sygnał audio, który składa się z idealnej sinusoidy o częstotliwości 5 kHz. Wiemy jak wygląda sinusoida w dziedzinie czasu, a w dziedzinie częstotliwości nie zobaczymy nic poza „piknięciem” częstotliwości przy 5 kHz. Załóżmy teraz, że włączymy oscylator o częstotliwości 500 kHz, który wprowadza szum o wysokiej częstotliwości do sygnału audio.

Sygnał widziany na oscyloskopie nadal będzie tylko jedną sekwencją napięć, z jedną wartością na moment czasu, ale sygnał będzie wyglądał inaczej, ponieważ jego zmiany w dziedzinie czasu muszą teraz odzwierciedlać zarówno sinusoidę o częstotliwości 5 kHz, jak i fluktuacje szumu o wysokiej częstotliwości.

W dziedzinie częstotliwości jednak, sinusoida i szum są oddzielnymi składowymi częstotliwości, które są obecne jednocześnie w tym jednym sygnale. Sinusoida i szum zajmują różne części reprezentacji sygnału w dziedzinie częstotliwości (jak pokazano na poniższym diagramie), a to oznacza, że możemy odfiltrować szum, kierując sygnał przez obwód, który przepuszcza niskie częstotliwości i blokuje wysokie częstotliwości.

Typy filtrów

Filtry można podzielić na szerokie kategorie, które odpowiadają ogólnej charakterystyce odpowiedzi częstotliwościowej filtra. Jeśli filtr przepuszcza niskie częstotliwości i blokuje wysokie częstotliwości, nazywany jest filtrem dolnoprzepustowym. Jeśli blokuje on niskie częstotliwości i przepuszcza wysokie, jest to filtr górnoprzepustowy. Istnieją również filtry pasmowo-przepustowe, które przepuszczają tylko stosunkowo wąski zakres częstotliwości, oraz filtry pasmowo-zaporowe, które blokują tylko stosunkowo wąski zakres częstotliwości.

Filtry można również sklasyfikować według typów komponentów, które są używane do realizacji obwodu. Filtry pasywne wykorzystują rezystory, kondensatory i cewki; komponenty te nie mają zdolności do zapewnienia wzmocnienia, a w konsekwencji filtr pasywny może jedynie utrzymać lub zmniejszyć amplitudę sygnału wejściowego. Filtr aktywny, z drugiej strony, może zarówno filtrować sygnał, jak i stosować wzmocnienie, ponieważ zawiera aktywny element, taki jak tranzystor lub wzmacniacz operacyjny.

Ten aktywny filtr dolnoprzepustowy jest oparty na popularnej topologii Sallen-Key.

Ten artykuł bada analizę i projektowanie pasywnych filtrów dolnoprzepustowych. Obwody te odgrywają ważną rolę w wielu różnych systemach i aplikacjach.

Filtr dolnoprzepustowy RC

Aby stworzyć pasywny filtr dolnoprzepustowy, musimy połączyć element rezystancyjny z elementem reaktywnym. Innymi słowy, potrzebujemy obwodu, który składa się z rezystora i albo kondensatora albo cewki. W teorii, topologia dolnoprzepustowa rezystor-induktor (RL) jest równoważna, pod względem zdolności filtrowania, topologii dolnoprzepustowej rezystor-kondensator (RC). W praktyce jednak, wersja rezystor-kondensator jest znacznie bardziej powszechna, a co za tym idzie, reszta tego artykułu skupi się na filtrze dolnoprzepustowym RC.

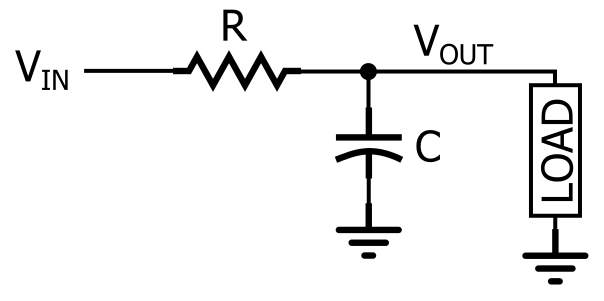
Filtr dolnoprzepustowy RC.

Jak widać na schemacie, odpowiedź dolnoprzepustowa RC jest tworzona przez umieszczenie rezystora w szeregu ze ścieżką sygnału i kondensatora równolegle z obciążeniem. Na schemacie obciążenie jest pojedynczym elementem, ale w rzeczywistym obwodzie może to być coś znacznie bardziej skomplikowanego, np. przetwornik analogowo-cyfrowy, wzmacniacz lub stopień wejściowy oscyloskopu, którego używasz do pomiaru odpowiedzi filtru.

Możemy intuicyjnie przeanalizować działanie filtrujące topologii dolnoprzepustowej RC, jeśli zauważymy, że rezystor i kondensator tworzą zależny od częstotliwości dzielnik napięcia.

Filtr dolnoprzepustowy RC przerysowany tak, aby wyglądał jak dzielnik napięcia.

Gdy częstotliwość sygnału wejściowego jest niska, impedancja kondensatora jest wysoka w stosunku do impedancji rezystora; dlatego większość napięcia wejściowego spada na kondensator (i na obciążenie, które jest równoległe do kondensatora). Kiedy częstotliwość wejściowa jest wysoka, impedancja kondensatora jest niska w stosunku do impedancji rezystora, co oznacza, że więcej napięcia spada przez rezystor, a mniej jest przekazywane do obciążenia. Tak więc, niskie częstotliwości są przekazywane i wysokie częstotliwości są blokowane.

To jakościowe wyjaśnienie RC funkcji dolnoprzepustowej jest ważnym pierwszym krokiem, ale nie jest to bardzo pomocne, gdy musimy faktycznie zaprojektować obwód, ponieważ terminy „wysoka częstotliwość” i „niska częstotliwość” są bardzo niejasne. Inżynierowie muszą tworzyć obwody, które przepuszczają i blokują określone częstotliwości. Na przykład, w systemie audio opisanym powyżej, chcemy zachować sygnał o częstotliwości 5 kHz i stłumić sygnał o częstotliwości 500 kHz. Oznacza to, że potrzebujemy filtra, który przechodzi od przepuszczania do blokowania gdzieś pomiędzy 5 kHz a 500 kHz.

Częstotliwo¶ć odcięcia

Zakres częstotliwo¶ci, dla których filtr nie powoduje znacz±cego tłumienia nazywany jest pasmem przepustowym, a zakres częstotliwo¶ci, dla których filtr powoduje znacz±ce tłumienie nazywany jest pasmem zaporowym. Filtry analogowe, takie jak filtr dolnoprzepustowy RC, zawsze przechodzą stopniowo od pasma przepustowego do pasma zaporowego. Oznacza to, że nie da się określić jednej częstotliwości, przy której filtr przestaje przepuszczać sygnały i zaczyna je blokować. Jednakże, inżynierowie potrzebują sposobu na wygodne i zwięzłe podsumowanie odpowiedzi częstotliwościowej filtra, i to jest miejsce, gdzie pojęcie częstotliwości odcięcia wchodzi do gry.

Gdy spojrzysz na wykres odpowiedzi częstotliwościowej filtra RC, zauważysz, że termin „częstotliwość odcięcia” nie jest bardzo dokładny. Obraz widma sygnału, który jest „cięty” na dwie połowy, z których jedna jest zachowywana, a druga odrzucana, nie ma zastosowania, ponieważ tłumienie wzrasta stopniowo, gdy częstotliwości przesuwają się od poniżej do powyżej częstotliwości odcięcia.

Częstotliwość odcięcia filtru dolnoprzepustowego RC jest w rzeczywistości częstotliwością, przy której amplituda sygnału wejściowego jest zmniejszona o 3 dB (wartość ta została wybrana, ponieważ zmniejszenie amplitudy o 3 dB odpowiada zmniejszeniu mocy o 50%). Dlatego też częstotliwość odcięcia jest również nazywana częstotliwością -3 dB i w rzeczywistości ta nazwa jest bardziej dokładna i bardziej informatywna. Termin szerokość pasma odnosi się do szerokości pasma przepustowego filtru, a w przypadku filtru dolnoprzepustowego szerokość pasma jest równa częstotliwości -3 dB (jak pokazano na poniższym wykresie).

Niniejszy wykres przedstawia ogólną charakterystykę odpowiedzi częstotliwościowej filtru dolnoprzepustowego RC. Szerokość pasma jest równa częstotliwości -3 dB.

Jak wyjaśniono powyżej, zachowanie dolnoprzepustowe filtru RC jest spowodowane interakcją pomiędzy impedancją rezystora niezależną od częstotliwości i impedancją kondensatora zależną od częstotliwości. Aby określić szczegóły odpowiedzi częstotliwościowej filtra, musimy matematycznie przeanalizować związek pomiędzy rezystancją (R) i pojemnością (C), a także możemy manipulować tymi wartościami w celu zaprojektowania filtra, który spełnia precyzyjne specyfikacje. Częstotliwość odcięcia (fC) filtru dolnoprzepustowego RC oblicza się w następujący sposób:

Patrzmy na prosty przykład projektowy. Wartości kondensatorów są bardziej restrykcyjne niż wartości rezystorów, więc zaczniemy od zwykłej wartości pojemności (np. 10 nF), a następnie użyjemy równania do określenia wymaganej wartości rezystancji. Celem jest zaprojektowanie filtra, który zachowa przebieg dźwiękowy o częstotliwości 5 kHz i odrzuci przebieg szumów o częstotliwości 500 kHz. Wypróbujemy częstotliwość odcięcia 100 kHz, a w dalszej części artykułu dokładniej przeanalizujemy wpływ tego filtru na te dwie składowe częstotliwości.

W ten sposób rezystor 160 Ω w połączeniu z kondensatorem 10 nF da nam filtr, który jest bardzo zbliżony do pożądanej odpowiedzi częstotliwościowej.

Obliczanie odpowiedzi filtra

Możemy obliczyć teoretyczne zachowanie filtra dolnoprzepustowego używając zależnej od częstotliwości wersji typowego dzielnika napięcia. Wyjście rezystancyjnego dzielnika napięcia jest wyrażone w następujący sposób:

Filtr RC używa równoważnej struktury, ale zamiast R2 mamy kondensator. Najpierw zamieniamy R2 (w liczniku) na reaktancję kondensatora (XC). Następnie musimy obliczyć wielkość impedancji całkowitej i umieścić ją w mianowniku. W ten sposób mamy

Reaktancja kondensatora wskazuje wielkość oporu dla przepływu prądu, ale w przeciwieństwie do rezystancji, wielkość oporu zależy od częstotliwości sygnału przechodzącego przez kondensator. Musimy więc obliczyć reaktancję przy określonej częstotliwości, a równanie, którego do tego używamy, jest następujące:

W powyższym przykładzie konstrukcyjnym, R ≈ 160 Ω i C = 10 nF. Przyjmiemy, że amplituda VIN wynosi 1 V, abyśmy mogli po prostu usunąć VIN z obliczeń. Najpierw obliczmy amplitudę VOUT przy częstotliwości fali sinusoidalnej:

Amplituda fali sinusoidalnej jest w zasadzie niezmieniona. To dobrze, ponieważ naszym zamiarem było zachowanie sinusoidy przy jednoczesnym tłumieniu szumu. Wynik ten nie jest zaskakujący, ponieważ wybraliśmy częstotliwość odcięcia (100 kHz), która jest znacznie wyższa niż częstotliwość sinusoidy (5 kHz).

Zobaczmy teraz, jak skutecznie filtr będzie tłumił składową szumu.

Amplituda szumu wynosi tylko około 20% swojej pierwotnej wartości.

Wizualizacja odpowiedzi filtru

Najwygodniejszym sposobem oceny wpływu filtru na sygnał jest zbadanie wykresu odpowiedzi częstotliwościowej filtru. Wykresy te, często nazywane wykresami Bode’a, mają wielkość (w decybelach) na osi pionowej i częstotliwość na osi poziomej; oś pozioma ma zazwyczaj skalę logarytmiczną, tak że fizyczna odległość między 1 Hz a 10 Hz jest taka sama jak fizyczna odległość między 10 Hz a 100 Hz, między 100 Hz a 1 kHz, i tak dalej. Taka konfiguracja pozwala nam szybko i dokładnie ocenić zachowanie filtra w bardzo dużym zakresie częstotliwości.

Przykład wykresu odpowiedzi częstotliwościowej.

Każdy punkt na krzywej wskazuje wielkość, jaką będzie miał sygnał wyjściowy, jeśli sygnał wejściowy ma wielkość 1 V i częstotliwość równą odpowiedniej wartości na osi poziomej. Na przykład, gdy częstotliwość wejściowa wynosi 1 MHz, amplituda wyjściowa (zakładając, że amplituda wejściowa wynosi 1 V) wyniesie 0,1 V (ponieważ -20 dB odpowiada dziesięciokrotnej redukcji).

Ogólny kształt tej krzywej odpowiedzi na częstotliwość stanie się bardzo znajomy, gdy spędzisz więcej czasu z obwodami filtrów. Krzywa jest prawie idealnie płaska w paśmie przepustowym, a następnie zaczyna opadać coraz szybciej, gdy częstotliwość wejściowa zbliża się do częstotliwości odcięcia. Ostatecznie szybkość zmiany tłumienia, zwana roll-off, stabilizuje się na poziomie 20 dB/dekadę – to znaczy, że wielkość sygnału wyjściowego jest zmniejszana o 20 dB na każdy czynnik dziesięciokrotnego wzrostu częstotliwości wejściowej.

Ocena wydajności filtra dolnoprzepustowego

Jeśli dokładnie wykreślimy odpowiedź częstotliwościową filtra, który zaprojektowaliśmy wcześniej w artykule, zobaczymy, że odpowiedź magnitudowa przy 5 kHz wynosi zasadniczo 0 dB (tzn, prawie zerowe tłumienie), a odpowiedź wielkości przy 500 kHz wynosi około -14 dB (co odpowiada wzmocnieniu 0,2). Wartości te są zgodne z wynikami obliczeń, które przeprowadziliśmy w poprzednim rozdziale.

Ponieważ filtry RC zawsze mają stopniowe przejście od pasma przepustowego do pasma zatrzymania, a tłumienie nigdy nie osiąga nieskończoności, nie możemy zaprojektować filtru „doskonałego” – to znaczy takiego, który nie ma żadnego wpływu na sinusoidę i całkowicie eliminuje szum. Zamiast tego, zawsze mamy do czynienia z kompromisem. Jeśli przesuniemy częstotliwość odcięcia bliżej 5 kHz, uzyskamy większe tłumienie szumu, ale również większe tłumienie fali sinusoidalnej, którą chcemy wysłać do głośnika. Jeśli przesuniemy częstotliwość odcięcia bliżej 500 kHz, będziemy mieli mniejsze tłumienie przy częstotliwości fali sinusoidalnej, ale także mniejsze tłumienie przy częstotliwości szumu.

Przesunięcie fazowe filtra dolnoprzepustowego

Do tej pory omówiliśmy sposób, w jaki filtr modyfikuje amplitudę różnych składowych częstotliwości w sygnale. Jednakże, reaktywne elementy obwodu zawsze wprowadzają przesunięcie fazowe oprócz efektów amplitudowych.

Pojęcie fazy odnosi się do wartości sygnału okresowego w określonym momencie cyklu. Tak więc, kiedy mówimy, że obwód powoduje przesunięcie fazowe, mamy na myśli, że tworzy on przesunięcie pomiędzy sygnałem wejściowym i wyjściowym: sygnały wejściowy i wyjściowy nie zaczynają i nie kończą już swoich cykli w tym samym momencie w czasie. Wartość przesunięcia fazowego, taka jak 45° lub 90°, wskazuje, jak duże przesunięcie zostało utworzone.

Każdy element reaktywny w obwodzie wprowadza 90° przesunięcia fazowego, ale to przesunięcie fazowe nie dzieje się jednocześnie. Faza sygnału wyjściowego, tak jak wielkość sygnału wyjściowego, zmienia się stopniowo wraz ze wzrostem częstotliwości wejściowej. W filtrze dolnoprzepustowym RC mamy jeden element reaktywny (kondensator), a w konsekwencji obwód ostatecznie wprowadzi 90° przesunięcia fazowego.

Jak w przypadku odpowiedzi magnitudowej, odpowiedź fazowa jest najłatwiejsza do oceny poprzez zbadanie wykresu, w którym oś pozioma oznacza częstotliwość logarytmiczną. Poniższy opis przedstawia ogólny wzór, a następnie można uzupełnić szczegóły poprzez zbadanie wykresu.

• Przesunięcie fazowe wynosi początkowo 0°.
• Stopniowo wzrasta, aż osiągnie 45° przy częstotliwości odcięcia; podczas tej części odpowiedzi, szybkość zmian jest rosnąca.
• Po przekroczeniu częstotliwości odcięcia przesunięcie fazowe nadal rośnie, ale szybkość zmian maleje.
• Szybkość zmian staje się bardzo mała, gdy przesunięcie fazowe zbliża się asymptotycznie do 90°.

Linia ciągła to odpowiedź wielkościowa, a linia kropkowana to odpowiedź fazowa. Częstotliwość odcięcia wynosi 100 kHz. Zauważ, że przesunięcie fazowe wynosi 45° przy częstotliwości odcięcia.

Filtry dolnoprzepustowe drugiego rzędu

Do tej pory założyliśmy, że filtr dolnoprzepustowy RC składa się z jednego rezystora i jednego kondensatora. Ta konfiguracja jest filtrem pierwszego rzędu.

„Rząd” filtru pasywnego jest określany przez liczbę elementów reaktywnych, tj. kondensatorów lub cewek, które są obecne w obwodzie. Filtr wyższego rzędu ma więcej elementów reaktywnych, a to prowadzi do większego przesunięcia fazowego i bardziej stromego tłumienia. Ta druga cecha jest główną motywacją do zwiększania rzędu filtra.

Dodając jeden element reaktywny do filtra – np. przechodząc z pierwszego rzędu do drugiego lub z drugiego rzędu do trzeciego – zwiększamy maksymalne tłumienie o 20 dB/dekadę. Bardziej strome tłumienie przekłada się na szybsze przejście od niskiego tłumienia do wysokiego tłumienia, a to może skutkować poprawą wydajności, gdy sygnał nie ma szerokiego pasma częstotliwości, które oddziela pożądane składowe częstotliwości od składowych szumu.

Filtry drugiego rzędu są powszechnie budowane wokół obwodu rezonansowego składającego się z cewki i kondensatora (ta topologia jest nazywana „RLC” od rezystor-induktor-kondensator). Jednakże, możliwe jest również tworzenie filtrów RC drugiego rzędu. Jak pokazano na poniższym schemacie, wszystko co musimy zrobić, to połączyć kaskadowo dwa filtry RC pierwszego rzędu.

Chociaż ta topologia z pewnością tworzy odpowiedź drugiego rzędu, nie jest ona szeroko stosowana – jak zobaczymy w następnej sekcji, odpowiedź częstotliwościowa jest często gorsza niż w przypadku filtru aktywnego drugiego rzędu lub filtru RLC drugiego rzędu.

Odpowiedź częstotliwościowa filtru RC drugiego rzędu

Możemy spróbować stworzyć filtr dolnoprzepustowy RC drugiego rzędu projektując filtr pierwszego rzędu zgodnie z pożądaną częstotliwością odcięcia, a następnie łącząc dwa z tych stopni pierwszego rzędu szeregowo. W ten sposób otrzymujemy filtr, który ma podobną ogólną charakterystykę częstotliwościową i maksymalne tłumienie 40 dB/dekadę zamiast 20 dB/dekadę.

Jednakże, jeśli przyjrzymy się dokładniej odpowiedzi, zauważymy, że częstotliwość -3 dB zmniejszyła się. Filtr RC drugiego rzędu nie zachowuje się zgodnie z oczekiwaniami, ponieważ te dwa stopnie nie są niezależne – nie możemy po prostu połączyć tych dwóch stopni razem i analizować obwodu jako filtr dolnoprzepustowy pierwszego rzędu, po którym następuje identyczny filtr dolnoprzepustowy pierwszego rzędu.

Co więcej, nawet jeśli wstawimy bufor pomiędzy te dwa stopnie, tak aby pierwszy stopień RC i drugi stopień RC mogły działać jako niezależne filtry, tłumienie przy oryginalnej częstotliwości odcięcia wyniesie 6 dB zamiast 3 dB. Dzieje się tak właśnie dlatego, że oba stopnie działają niezależnie – pierwszy filtr ma 3 dB tłumienia przy częstotliwości odcięcia, a drugi dodaje kolejne 3 dB tłumienia.

Podstawowym ograniczeniem filtru dolnoprzepustowego RC drugiego rzędu jest to, że projektant nie może precyzyjnie dostroić przejścia z pasma przepustowego do pasma zaporowego poprzez regulację współczynnika Q filtra; parametr ten określa, jak bardzo tłumiona jest odpowiedź częstotliwościowa. W przypadku kaskadowego połączenia dwóch identycznych filtrów dolnoprzepustowych RC, ogólna funkcja przenoszenia odpowiada odpowiedzi drugiego rzędu, ale współczynnik Q wynosi zawsze 0,5. Gdy Q = 0,5, filtr znajduje się na granicy nadmiernego tłumienia, a to skutkuje charakterystyką częstotliwościową, która „zwisa” w obszarze przejściowym. Filtry aktywne drugiego rzędu i filtry oparte na rezonansie drugiego rzędu nie mają tego ograniczenia; projektant może kontrolować współczynnik Q i w ten sposób precyzyjnie dostroić odpowiedź częstotliwościową w obszarze przejściowym.

Podsumowanie

• Wszystkie sygnały elektryczne zawierają mieszaninę pożądanych składowych częstotliwości i niepożądanych składowych częstotliwości. Niepożądane składowe częstotliwości są zwykle powodowane przez szumy i zakłócenia, a w niektórych sytuacjach negatywnie wpływają na działanie systemu.
• Filtr to obwód, który reaguje w różny sposób na różne części widma sygnału. Filtr dolnoprzepustowy jest przeznaczony do przepuszczania składowych o niskiej częstotliwości i blokowania składowych o wysokiej częstotliwości.
• Częstotliwość odcięcia filtra dolnoprzepustowego wskazuje obszar częstotliwości, w którym filtr przechodzi od niskiego tłumienia do znacznego tłumienia.
• Napięcie wyjściowe filtru dolnoprzepustowego RC można obliczyć traktując obwód jako dzielnik napięcia składający się z rezystancji (niezależnej od częstotliwości) i reaktancji (zależnej od częstotliwości).
• Wykres wielkości (w dB, na osi pionowej) w stosunku do częstotliwości logarytmicznej (w hercach, na osi poziomej) jest wygodnym i efektywnym sposobem badania teoretycznego zachowania filtru. Można również użyć wykresu fazy względem częstotliwości logarytmicznej, aby określić wielkość przesunięcia fazowego, które zostanie zastosowane do sygnału wejściowego.
• Filtr drugiego rzędu zapewnia bardziej strome tłumienie; ta odpowiedź drugiego rzędu jest pomocna, gdy sygnał nie zapewnia szerokiego pasma separacji pomiędzy pożądanymi składowymi częstotliwości i niepożądanymi składowymi częstotliwości.
• Można utworzyć filtr dolnoprzepustowy RC drugiego rzędu, budując dwa identyczne filtry dolnoprzepustowe RC pierwszego rzędu, a następnie podłączając wyjście jednego z nich do wejścia drugiego. Całkowita częstotliwość -3 dB będzie niższa niż oczekiwana.

.