Co to jest sztuczka z jądrem? Dlaczego jest ważny?

Gdy mówimy o jądrach w uczeniu maszynowym, najprawdopodobniej pierwszą rzeczą, która przychodzi nam do głowy jest model maszyny wektorów nośnych (SVM), ponieważ sztuczka z jądrem jest szeroko stosowana w modelu SVM, aby połączyć liniowość i nieliniowość.

Aby pomóc Ci zrozumieć, czym jest jądro i dlaczego jest ważne, przedstawię najpierw podstawy modelu SVM.

Model SVM jest modelem nadzorowanego uczenia maszynowego, który jest głównie używany do klasyfikacji (ale może być również używany do regresji!). Uczy się on jak oddzielać różne grupy poprzez tworzenie granic decyzyjnych.

Na powyższym wykresie zauważamy, że istnieją dwie klasy obserwacji: punkty niebieskie i punkty fioletowe. Istnieje mnóstwo sposobów na rozdzielenie tych dwóch klas, jak pokazano na wykresie po lewej stronie. My jednak chcemy znaleźć „najlepszą” hiperpłaszczyznę, która zmaksymalizuje margines między tymi dwiema klasami, co oznacza, że odległość między hiperpłaszczyzną a najbliższymi punktami danych po każdej stronie jest największa. W zależności od tego, po której stronie hiperpłaszczyzny znajduje się nowy punkt danych, możemy przypisać klasę do nowej obserwacji.

W powyższym przykładzie brzmi to prosto. Jednakże, nie wszystkie dane są liniowo separowalne. W rzeczywistości, w prawdziwym świecie, prawie wszystkie dane są losowo rozmieszczone, co utrudnia liniowe rozdzielenie różnych klas.

Dlaczego ważne jest stosowanie sztuczki z jądrem?

Jak widać na powyższym rysunku, jeśli znajdziemy sposób na zmapowanie danych z przestrzeni dwuwymiarowej do przestrzeni trójwymiarowej, będziemy w stanie znaleźć powierzchnię decyzyjną, która wyraźnie dzieli na różne klasy. Moją pierwszą myślą o tym procesie transformacji danych jest mapowanie wszystkich punktów danych do wyższego wymiaru (w tym przypadku 3 wymiarowego), znalezienie granicy i dokonanie klasyfikacji.

To brzmi dobrze. Jednak, gdy jest coraz więcej wymiarów, obliczenia w tej przestrzeni stają się coraz droższe. Wtedy właśnie pojawia się sztuczka z jądrem. Pozwala nam ona operować w oryginalnej przestrzeni cech bez konieczności obliczania współrzędnych danych w przestrzeni o wyższych wymiarach.

Przyjrzyjrzyjmy się przykładowi:

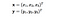
Tutaj x i y są dwoma punktami danych w 3 wymiarach. Załóżmy, że musimy zmapować x i y do przestrzeni 9-wymiarowej. Musimy wykonać następujące obliczenia, aby uzyskać ostateczny wynik, który jest po prostu skalarem. Złożoność obliczeniowa, w tym przypadku, wynosi O(n²).

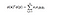
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).

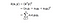
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Wszelkie obliczenia wykorzystujące produkty kropkowe (x, y) mogą wykorzystać sztuczkę z jądrem.

Różne funkcje jądra

Istnieją różne jądra. Najpopularniejsze z nich to wielomianowe i RBF (radial basis function).

„Intuicyjnie, wielomianowe jądro patrzy nie tylko na dane cechy próbek wejściowych w celu określenia ich podobieństwa, ale także na ich kombinacje” (Wikipedia), tak jak w przykładzie powyżej. Z n oryginalnymi cechami i d stopniami wielomianu, wielomianowe jądro daje n^d rozszerzonych cech.

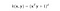
Kernel RBF nazywany jest również jądrem gaussowskim. Istnieje nieskończona liczba wymiarów w przestrzeni cech, ponieważ może być ona rozszerzona przez szereg Taylora. W poniższym formacie, parametr γ określa jak duży wpływ ma pojedynczy przykład treningowy. Im jest on większy, tym bliżej innych przykładów musi się znajdować, aby mieć na nie wpływ (dokumentacja sklearn).

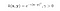
W bibliotece sklearn w Pythonie istnieją różne opcje dla funkcji jądra. Możesz nawet zbudować niestandardowe jądro w razie potrzeby.

Koniec

Trick z jądrem brzmi jak „doskonały” plan. Jednak jedną krytyczną rzeczą, o której należy pamiętać jest to, że kiedy mapujemy dane do wyższego wymiaru, są szanse, że możemy przepasować model. Dlatego wybór właściwej funkcji jądra (w tym właściwych parametrów) i regularności są bardzo ważne.

Jeśli jesteś ciekawy czym jest regularność, napisałem artykuł mówiący o moim rozumieniu tego zagadnienia i możesz go znaleźć tutaj.

Mam nadzieję, że podoba Ci się ten artykuł. Jak zawsze, proszę dać mi znać, jeśli masz jakieś pytania, komentarze, sugestie itp. Dzięki za przeczytanie 🙂