dB: Co to jest decybel?

Ciśnienie dźwięku, poziom dźwięku i dB. Dźwięk jest zwykle mierzony za pomocą mikrofonów, które reagują proporcjonalnie do ciśnienia akustycznego, p. Teraz moc w fali dźwiękowej, wszystko inne równe, idzie jako kwadrat ciśnienia. (Podobnie moc elektryczna w oporniku jest równa kwadratowi napięcia). Log x2 to po prostu 2 log x, więc wprowadza to współczynnik 2, gdy przeliczamy stosunek ciśnienia na decybele. Różnica w poziomie ciśnienia akustycznego pomiędzy dwoma dźwiękami o p1 i p2 wynosi zatem:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (przez cały czas log jest do podstawy 10).

Co się stanie, gdy zmniejszymy moc dźwięku o połowę? Logarytm z 2 wynosi 0,3010, więc logarytm z 1/2 wynosi -0,3, z dobrym przybliżeniem. Tak więc, jeśli zmniejszysz moc o połowę, zmniejszysz moc i poziom dźwięku o 3 dB. Zmniejszając ją ponownie o połowę (do 1/4 pierwotnej mocy), zmniejszamy poziom o kolejne 3 dB. Jeśli nadal będziesz zmniejszać moc o połowę, będziesz mieć takie proporcje.

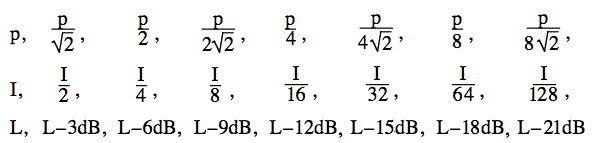
Co się stanie, jeśli dodam dwa identyczne dźwięki? Czy podwajam natężenie (wzrost o 3 dB)? Albo czy podwajam ciśnienie (wzrost o 6 dB)? To często zadawane pytanie jest nieco subtelne, więc zostało omówione tutaj w naszym FAQ.

Pliki dźwiękowe, aby pokazać wielkość decybela

Widzieliśmy powyżej, że zmniejszenie mocy o połowę zmniejsza ciśnienie akustyczne o √2, a poziom dźwięku o 3 dB. To właśnie zrobiliśmy w pierwszej grafice i pliku dźwiękowym poniżej.

Pierwsza próbka dźwięku to biały szum (mieszanina szerokiego zakresu słyszalnych częstotliwości, analogicznie do białego światła, które jest mieszaniną wszystkich widzialnych częstotliwości). Druga próbka to ten sam szum, ale o napięciu zmniejszonym o współczynnik √2. Teraz 1/√2 wynosi około 0,7, więc -3 dB odpowiada zmniejszeniu napięcia lub ciśnienia do 70% oryginalnej wartości. Zielona linia pokazuje napięcie jako funkcję czasu. Czerwona linia pokazuje ciągły rozkład wykładniczy w czasie. Zauważ, że napięcie spada o 50% na każdą drugą próbkę. Zauważ również, że podwojenie mocy nie robi wielkiej różnicy w głośności. Omówimy to dokładniej poniżej, ale warto o tym pamiętać przy wyborze sprzętu do odtwarzania dźwięku. Pliki dźwiękowe i animacja autorstwa Johna Tanna i George’a Hatsidimitrisa.

Jak duży jest decybel? W następnej serii kolejne próbki są zmniejszane tylko o jeden decybel.

Jeden decybel jest tego samego rzędu co Just Noticeable Difference (JND) dla poziomu dźwięku. Kiedy słuchasz tych plików, zauważysz, że ostatni jest cichszy niż pierwszy, ale jest to raczej mniej jasne dla ucha, że drugi z każdej pary jest cichszy niż jego poprzednik. 10*log10(1,26) = 1, więc aby zwiększyć poziom dźwięku o 1 dB, należy zwiększyć moc o 26% lub napięcie o 12%.

A co jeśli różnica jest mniejsza niż decybel? Poziomy dźwięku rzadko podaje się z dokładnością do części dziesiętnych. Powodem jest to, że poziomy dźwięku, które różnią się o mniej niż 1 dB są trudne do odróżnienia, jak pokazuje następny przykład.(To sprawia, że dB jest wygodną jednostką wielkości.)

0,3 dB kroki. Można zauważyć, że ostatni jest cichszy od pierwszego, ale trudno jest zauważyć różnicę między kolejnymi parami. 10*log10(1,07) = 0,3, a więc aby zwiększyć poziom dźwięku o 0,3 dB, należy zwiększyć moc o 7% lub napięcie o 3,5%.

Standardowe poziomy odniesienia. („absolutny” poziom dźwięku)

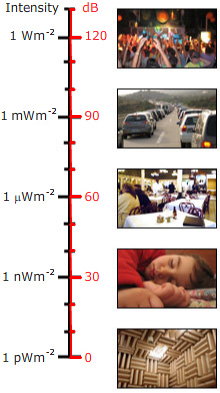Powiedzieliśmy powyżej, że decybel jest stosunkiem. Tak więc, gdy jest on używany do podawania poziomu dźwięku dla pojedynczego dźwięku, a nie jako stosunek, należy wybrać poziom odniesienia. Dla poziomu ciśnienia akustycznego, poziom odniesienia (dla powietrza) jest zwykle wybierany jako pref = 20 mikropaskali (20 μPa), lub 0,02 mPa. Jest to bardzo niska wartość: wynosi 2 dziesięciomiliardowe części atmosfery. Niemniej jednak, jest to mniej więcej granica czułości ludzkiego ucha, w jego wrażliwym zakresie częstotliwości. (Zwykle ta wrażliwość występuje tylko u ludzi młodych lub tych, którzy nie byli narażeni na głośną muzykę lub inne głośne dźwięki. Osobiste systemy muzyczne z głośnikami dousznymi są zdolne do bardzo wysokich poziomów dźwięku w uchu i są uważane przez niektórych za odpowiedzialne za wiele z utraty słuchu u młodych dorosłych w niektórych krajach).

Jeśli więc czytamy o poziomie ciśnienia akustycznego 86 dB, oznacza to, że

20 log (p2/pref) = 86 dB

gdzie pref to ciśnienie akustyczne poziomu odniesienia, a p2 to ciśnienie akustyczne danego dźwięku. Dzielimy obie strony przez 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 to logarytm 10 tysięcy, 0,3 to logarytm 2, więc ten dźwięk ma ciśnienie akustyczne 20 tysięcy razy większe niż poziom odniesienia (p2/pref = 20 000) lub natężenie 400 milionów razy większe niż poziom odniesienia. Dźwięk o natężeniu 86 dB jest głośny, ale nie jest niebezpieczny – pod warunkiem, że ekspozycja jest krótka.

Co oznacza 0 dB? Poziom ten występuje, gdy zmierzone natężenie dźwięku jest równe poziomowi odniesienia, tzn. jest to poziom dźwięku odpowiadający ciśnieniu 0,02 mPa. W tym przypadku mamy

Poziom dźwięku = 20 log (pmeasured/pref) = 20 log 1 = 0 dB

Pamiętajmy, że decybele mierzą stosunek. 0 dB występuje, gdy przyjmiemy logarytm stosunku równy 1 (log 1 = 0). Tak więc 0 dB nie oznacza braku dźwięku, oznacza poziom dźwięku, w którym ciśnienie akustyczne jest równe ciśnieniu poziomu odniesienia. Jest to małe ciśnienie, ale nie zerowe. Możliwe są również ujemne poziomy dźwięku: – 20 dB oznaczałoby dźwięk o ciśnieniu 10 razy mniejszym niż ciśnienie odniesienia, czyli 2 μPa.

Nie wszystkie ciśnienia akustyczne są jednakowo głośne. Dzieje się tak, ponieważ ludzkie ucho nie reaguje jednakowo na wszystkie częstotliwości: jesteśmy znacznie bardziej wrażliwi na dźwięki w zakresie częstotliwości od około 1 kHz do 7 kHz (1000 do 7000 drgań na sekundę) niż na dźwięki o bardzo niskiej lub wysokiej częstotliwości. Z tego powodu mierniki dźwięku są zwykle wyposażone w filtr, którego reakcja na częstotliwość jest nieco podobna do reakcji ludzkiego ucha. (Więcej o tych filtrach poniżej.) Jeśli używany jest „filtr ważący A”, poziom ciśnienia akustycznego podawany jest w jednostkach dB(A) lub dBA. Poziom ciśnienia akustycznego w skali dBA jest łatwy do zmierzenia i dlatego jest powszechnie stosowany. Jednym z powodów, dla których różni się on od głośności, jest fakt, że filtr nie reaguje w taki sam sposób jak ucho. Aby zrozumieć głośność dźwięku, należy najpierw zapoznać się z krzywymi przedstawiającymi charakterystykę częstotliwościową ludzkiego ucha, które podano poniżej. (Innym powodem jest to, że ludzki słuch nie jest logarytmiczny.

Miary logarytmiczne

Dlaczego używamy decybeli? Ucho jest w stanie usłyszeć bardzo duży zakres dźwięków: stosunek ciśnienia akustycznego, które powoduje trwałe uszkodzenie w wyniku krótkiej ekspozycji do granicy, którą (nieuszkodzone) uszy mogą usłyszeć, wynosi ponad milion. Aby poradzić sobie z takim zakresem, przydatne są jednostki logarytmiczne: logarytm miliona wynosi 6, więc ten stosunek reprezentuje różnicę 120 dB. Słuch nie jest z natury logarytmiczny w odpowiedzi. (Miary logarytmiczne są również przydatne, gdy dźwięk (krótko) wzrasta lub maleje wykładniczo w czasie. Dzieje się tak w wielu zastosowaniach obejmujących proporcjonalne wzmocnienie lub proporcjonalną stratę.)

Filtry używane dla dBA i dB(C)

Najpowszechniej używanym filtrem poziomu dźwięku jest skala A, która w przybliżeniu odpowiada odwrotności krzywej równej głośności 40 dB (przy 1 kHz). Przy użyciu tego filtra miernik poziomu dźwięku jest więc mniej wrażliwy na bardzo wysokie i bardzo niskie częstotliwości. Pomiary dokonywane w tej skali wyrażane są w dBA. Skala C zmienia się w niewielkim stopniu na przestrzeni kilku oktaw i dlatego nadaje się do subiektywnych pomiarów tylko dla umiarkowanych i wysokich poziomów dźwięku. Pomiary dokonywane w tej skali wyrażane są jako dB(C). Istnieje również (rzadko używana) skala wagowa B, pośrednia między A i C. Poniższy rysunek przedstawia odpowiedź filtra A (po lewej) i filtra C, ze wzmocnieniem w dB w odniesieniu do 1 kHz. (Wprowadzenie do filtrów, patrz: filtry RC, integratory i różniczkowniki).



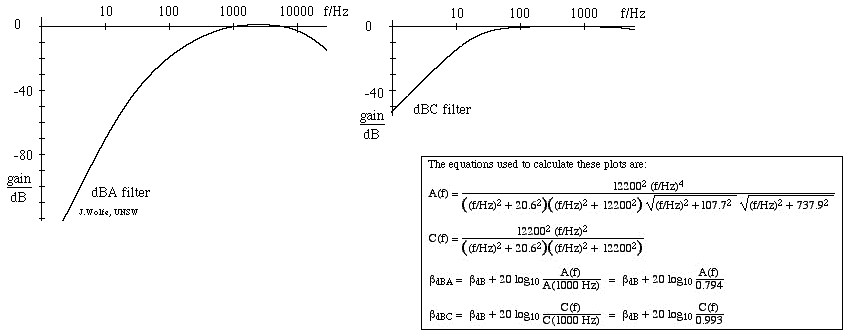
Na stronach poświęconych akustyce muzyki i akustyce mowy, widma dźwięku są podawane w dB. Powodem tej powszechnej praktyki jest fakt, że zakres mierzonych ciśnień akustycznych jest duży.

Pomiary dB(G) wykorzystują wąskopasmowy filtr, który nadaje wysoką wagę częstotliwościom pomiędzy 1 a 20 Hz, a niską pozostałym. W ten sposób uzyskuje się duże wartości dla dźwięków i infradźwięków, które nie są łatwo słyszalne. ISO 7196:1995

Głośność, fony i sony, krzywe odpowiedzi słuchowej

Fon jest jednostką, która jest związana z dB przez psychofizycznie mierzoną odpowiedź częstotliwościową ucha. Przy 1 kHz, odczyty w fonach i dB są z definicji takie same. Dla wszystkich innych częstotliwości, skala fonowa jest określana na podstawie wyników eksperymentów, w których ochotnicy byli proszeni o dostosowanie głośności sygnału o danej częstotliwości, aż ocenili jego głośność jako równą głośności sygnału o częstotliwości 1 kHz. Aby przeliczyć z dB na phony, potrzebny jest wykres takich wyników. Taki wykres zależy od poziomu dźwięku: staje się bardziej płaski przy wysokich poziomach dźwięku.

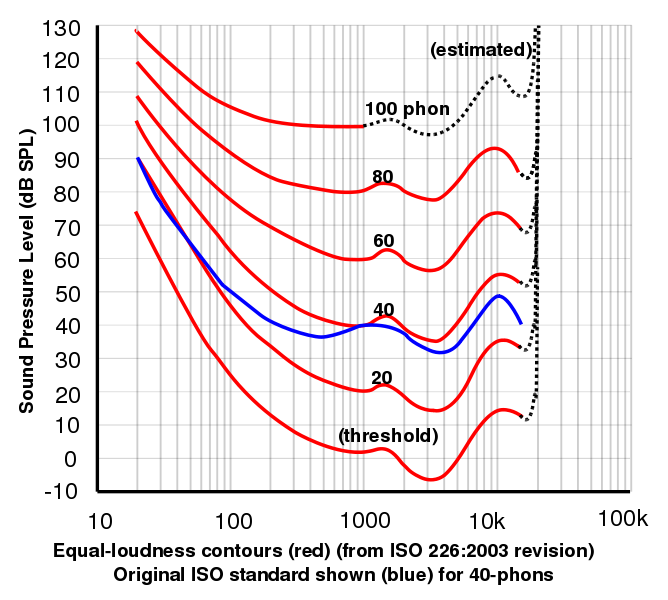
Ten wykres, dzięki uprzejmości Lindosland, przedstawia dane z 2003 roku z Międzynarodowej Organizacji Normalizacyjnej dla krzywych równej głośności wyznaczonych doświadczalnie. Wykresy równej głośności jako funkcji częstotliwości są często ogólnie nazywane krzywymi Fletchera-Munsona po oryginalnej pracy Fletchera, H. i Munsona, W.A. (1933) J.Acoust.Soc.Am. 6:59. Możesz stworzyć swoje własne krzywe korzystając z naszej strony poświęconej odpowiedziom słuchowym.

Son pochodzi z pomiarów psychofizycznych, w których ochotnicy dostosowywali dźwięki do tego, że oceniali je jako dwa razy głośniejsze. Pozwala to na odniesienie postrzeganej głośności do fonów. Jeden sone jest definiowany jako równy 40 fonom. Eksperymentalnie ustalono, że powyżej 40 fonów wzrost poziomu dźwięku o 10 dB odpowiada w przybliżeniu postrzeganemu podwojeniu głośności. Tak więc to przybliżenie jest używane w definicji sonu: 1 son = 40 fonów, 2 sony = 50 fonów, 4 sony = 60 fonów, itd.



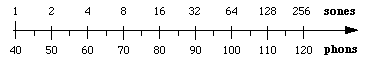
Zależność ta implikuje, że głośność i natężenie dźwięku są powiązane przez prawo potęgowe: głośność w sone jest proporcjonalna do (natężenie)log 2 = (natężenie)0.3.

Czy nie byłoby wspaniale móc konwertować z dB (które mogą być mierzone przez przyrząd) na tony (które przybliżają głośność postrzeganą przez ludzi)? Czasem robi się to za pomocą tabel, które można znaleźć w podręcznikach akustyki. Jeśli jednak nie masz nic przeciwko dość prymitywnemu przybliżeniu, możesz powiedzieć, że krzywa ważenia A przybliża ludzką odpowiedź częstotliwościową przy niskich i umiarkowanych poziomach dźwięku, więc dB(A) jest w przybliżeniu taka sama jak fony, w ograniczonym zakresie niskich poziomów. Następnie można użyć logarytmicznej relacji między tonami i fonami opisanej powyżej.

Poziom nagrywania i decybele

Mierniki mierzące poziom nagrywania lub poziom wyjściowy w elektronicznym sprzęcie audio (konsolety mikserskie itp.) prawie zawsze rejestrują napięcie AC rms (zobacz linki, aby dowiedzieć się o AC i rms). Dla danego rezystora R, moc P wynosi V2/R, więc
różnica w poziomie napięcia = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, lub

absolutny poziom napięcia = 20 log (V/Vref)

gdzie Vref jest napięciem odniesienia. Jakie jest więc napięcie odniesienia?

Oczywistym poziomem do wyboru jest jeden wolt rms, i w tym przypadku poziom jest zapisywany jako dBV. Jest to racjonalne, a także wygodne w przypadku kart analogowo-cyfrowych, których maksymalny zakres często wynosi około jednego wolta rms. Trzeba więc pamiętać, aby poziom był ujemny w dBV (mniej niż jeden wolt), aby uniknąć obcinania szczytów sygnału, ale nie za bardzo ujemny (aby nasz sygnał był nadal dużo większy od szumu tła).

Niekiedy zobaczysz dBm. Kiedyś oznaczało to decybele mocy elektrycznej, w odniesieniu do jednego miliwata, i czasami nadal tak jest. Jednakże, jest to skomplikowane z powodów historycznych. W połowie XX wieku wiele linii audio miało impedancję znamionową 600 Ω. Jeśli impedancja jest czysto rezystancyjna, i jeśli ustawimy V2/600 Ω = 1 mW, to otrzymamy V = 0,775 V. Tak więc, zakładając, że używasz obciążenia 600 Ω, 1 mW mocy to 0 dBm, czyli 0,775 V, więc tak kalibrowałeś swoje mierniki poziomu. Problem pojawił się, ponieważ gdy miernik poziomu mierzący napięcie jest skalibrowany w ten sposób, będzie odczytywał 0 dBm przy 0,775 V, nawet jeśli nie jest podłączony do 600 Ω. Tak więc, być może nielogicznie, dBm będzie czasami oznaczał dB w odniesieniu do 0,775 V. (Kiedy byłem chłopcem, kalkulatory były drogie, więc używałem starej suwmiarki taty, która miała współczynnik 0,775 zaznaczony na okienku kursora, aby ułatwić takie obliczenia).

Jak przeliczyć dBV lub dBm na dB poziomu dźwięku? Nie ma prostego sposobu. Wszystko zależy od tego, w jaki sposób zamieniamy moc elektryczną na moc akustyczną. Nawet jeśli sygnał elektryczny jest podłączony bezpośrednio do głośnika, konwersja będzie zależeć od wydajności i impedancji głośnika. I oczywiście może istnieć wzmacniacz mocy i różne komplikacje akustyczne pomiędzy miejscem, w którym mierzysz dBV na pulpicie mikserskim, a miejscem, w którym znajdują się twoje uszy w polu dźwiękowym.

Intensywność, promieniowanie i dB

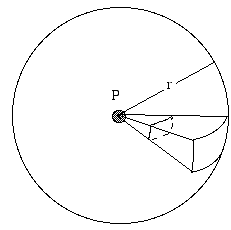
Jak poziom dźwięku (lub poziom sygnału radiowego, itp.) zależy od odległości od źródła?

Źródło, które emituje promieniowanie jednakowo we wszystkich kierunkach nazywamy izotropowym. Rozważmy izolowane źródło dźwięku, z dala od wszelkich powierzchni odbijających – może to być ptak śpiewający wysoko w powietrzu. Wyobraźmy sobie kulę o promieniu r, której środek znajduje się na źródle. Źródło emituje całkowitą moc P, w sposób ciągły. Ta moc akustyczna rozchodzi się i przechodzi przez powierzchnię kuli. Jeśli źródło jest izotropowe, natężenie I jest z definicji takie samo w każdym miejscu na tej powierzchni. Natężenie I definiuje się jako moc na jednostkę powierzchni. Pole powierzchni kuli wynosi 4πr2, więc moc (w naszym przykładzie moc dźwięku) przechodząca przez każdy metr kwadratowy powierzchni jest z definicji taka sama:

I = P/4πr2.

Widzimy więc, że dla źródła izotropowego natężenie jest odwrotnie proporcjonalne do kwadratu odległości od źródła:

I2/I1 = r12/r22.

Ale natężenie jest proporcjonalne do kwadratu ciśnienia akustycznego, więc równie dobrze moglibyśmy napisać:

p2/p1 = r1/r2.

Jeśli więc podwoimy odległość, zmniejszymy ciśnienie akustyczne o współczynnik 2, a natężenie o współczynnik 4: innymi słowy, zmniejszymy poziom dźwięku o 6 dB. Jeśli zwiększymy r o współczynnik 10, zmniejszymy poziom o 20 dB, itd.

Należy jednak pamiętać, że wiele źródeł nie jest izotropowych, zwłaszcza jeśli długość fali jest mniejsza niż, lub o wielkości porównywalnej ze źródłem. Ponadto, odbicia są często dość ważne, zwłaszcza jeśli ziemia jest w pobliżu, lub jeśli jesteś w pomieszczeniach zamkniętych.

Ciśnienie, natężenie i impedancja właściwa

Dla fal akustycznych, właściwa impedancja akustyczna z jest definiowana jako stosunek ciśnienia akustycznego p do średniej prędkości cząstek u, ze względu na dźwięk ave, z = p/u . W Impedancja akustyczna, natężenie i moc pokazujemy, jak powiązać ciśnienie akustyczne RMS p i natężenie I:
I = p2/z

Dla powietrza, właściwa impedancja akustyczna z wynosi 420 kg.s-1.m-2 = 420 Pa.s.m-1. Dla wody (słodkiej), właściwa impedancja akustyczna dla wody wynosi 1.48 MPa.s.m-1. Tak więc fala dźwiękowa w wodzie o tym samym ciśnieniu ma znacznie mniejsze natężenie niż w powietrzu.

dBi i promieniowanie, które zmienia się w zależności od kierunku

Promieniowanie, które zmienia się w zależności od kierunku jest nazywane anizotropowym. W wielu przypadkach w komunikacji, promieniowanie izotropowe jest marnotrawstwem: po co emitować znaczną część mocy w górę, jeśli odbiornik jest, tak jak Ty, stosunkowo blisko poziomu gruntu. Dla dźwięku o krótkiej długości fali (w tym większość zakresu ważnego dla mowy), megafon może pomóc uczynić twój głos bardziej anizotropowym. Dla radia, szeroki zakres projektów pozwala anteny być wysoce anizotropowe zarówno dla transmisji i odbioru.

Więc, gdy jesteś zainteresowany w emisji w (lub odbioru z) określonym kierunku, chcesz stosunek intensywności mierzonej w tym kierunku, w danej odległości, aby być wyższa niż ta mierzona w tej samej odległości od izotropowego grzejnika (lub odbierane przez odbiornik izotropowy). Stosunek ten nazywany jest zyskiem; wyrażając stosunek w dB otrzymujemy zysk w dBi dla danego promiennika. Jednostka ta jest używana głównie w antenach, zarówno nadawczych jak i odbiorczych, ale czasami jest używana w przypadku źródeł dźwięku i mikrofonów kierunkowych.

Przykładowe problemy

Kilka osób pisało z prośbą o przykłady użycia dB w obliczeniach. A więc…
• Jak głośniejszy jest głośnik wysterowany (w zakresie liniowym) przez wzmacniacz o mocy 100 W niż przez wzmacniacz o mocy 10 W?

  Moce te różnią się o współczynnik dziesięciokrotny, który, jak widzieliśmy powyżej, wynosi 10 dB. Wszystkie inne równe oznacza, że odpowiedzi częstotliwościowe są równe i że używany jest ten sam sygnał wejściowy, itd. Tak więc zależność częstotliwościowa powinna być taka sama. 10 dB odpowiada 10 fonom. Aby uzyskać odczuwalne podwojenie głośności, potrzebny jest wzrost o 10 fonów. Tak więc głośnik wysterowany przez wzmacniacz 100 W jest dwa razy głośniejszy niż wysterowany przez wzmacniacz 10 W, zakładając, że pozostajemy w zakresie liniowym i nie zniekształcamy ani nie niszczymy głośnika. (Wzmacniacz 100 W wytwarza dwa razy więcej tonów niż wzmacniacz 10 W.)

• Staję w odległości R od małego źródła dźwięku (o wielkości znacznie mniejszej niż R), na poziomie gruntu, na otwartej przestrzeni, gdzie odbicia mogą być zaniedbane. Poziom dźwięku wynosi L. Jeśli teraz przesunę się na odległość nR (n jest liczbą, a nR nadal jest znacznie większe niż wielkość źródła), jaki będzie nowy poziom dźwięku?

  Po pierwsze, zauważ, że zaniedbanie odbić jest bardzo ważne. To obliczenie nie będzie działać wewnątrz pomieszczenia, gdzie odbicia od ścian (zbiorczo wytwarzające pogłos) utrudniają obliczenia. Na otwartej przestrzeni, natężenie dźwięku jest proporcjonalne do 1/r2, gdzie r jest odległością od źródła. (Stała proporcjonalności zależy od tego, jak dobrze odbija się ziemia, i nie dotyczy nas tutaj, ponieważ będzie ona z grubsza anulowana w obliczeniach, pod warunkiem, że r jest rozsądnie duże). Zatem, jeśli zwiększymy r z R do nR, zmniejszymy natężenie z I do I/n 2.

  Różnica w decybelach pomiędzy dwoma sygnałami o natężeniu I 2 i I 1 jest zdefiniowana powyżej jako

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Na przykład, jeśli n wynosi 2 (tzn. jeśli jesteśmy dwa razy dalej), intensywność jest zmniejszona czterokrotnie, a poziom dźwięku spada z L do (L – 6dB).

• Jeśli w idealnie cichych warunkach młoda osoba słyszy dźwięk o częstotliwości 1 kHz i natężeniu 0 dB emitowany przez głośnik (może miękki?), o ile należy zwiększyć moc głośnika, aby dźwięk osiągnął poziom 110 dB (poziom niebezpiecznie głośny, ale możliwy do przeżycia)?

  Różnica w decybelach pomiędzy dwoma sygnałami o mocach P2 i P1 jest zdefiniowana powyżej jako

  ΔL = 10 log (P2/P1) dB więc, podnosząc 10 do potęgi tych dwóch równych wielkości:
  10L/10 = P2/P1 więc:
  P2/P1 = 10110/10 = 1011 = sto tysięcy milionów.

  co jest dowodem na to, że ludzkie ucho ma niezwykle duży zakres dynamiki, być może większy niż oko.

• Wzmacniacz ma na wejściu 10 mV, a na wyjściu 2 V. Jakie jest jego wzmocnienie napięciowe w dB?

  Napięcie, podobnie jak ciśnienie, pojawia się podniesione do kwadratu w wyrażeniach dotyczących mocy lub natężenia. (Moc rozpraszana w oporniku R to V2/R.) Tak więc, umownie, definiujemy:

  gain = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (W podanych powyżej przypadkach akustycznych widzieliśmy, że stosunek ciśnienia, wyrażony w dB, był taki sam jak stosunek mocy: to był powód zastosowania czynnika 20 przy definiowaniu dB dla ciśnienia. Warto zauważyć, że w przykładzie ze wzmocnieniem napięciowym, wzmocnienie mocy wzmacniacza raczej nie będzie równe wzmocnieniu napięciowemu, które jest zdefiniowane przez zastosowaną tu konwencję. Moc jest proporcjonalna do kwadratu napięcia na danym oporniku. Jednakże impedancje wejściowe i wyjściowe wzmacniaczy są często zupełnie inne. Na przykład, wzmacniacz buforowy lub wtórnik emiterowy ma wzmocnienie napięciowe około 1, ale duże wzmocnienie prądowe).

• Jaka jest różnica w dB między natężeniem światła na Ziemi (8,3 minut świetlnych od Słońca) i na Uranie (160 minut świetlnych)?

  Podobnie jak dźwięk, izotropowe natężenie światła maleje jako r-2, więc stosunek natężenia wynosi (160/8.3)2 = 20 log (160/8.3) = 26 dB.

Zdrowie i bezpieczeństwo pracy

Różne kraje i prowincje mają oczywiście różne przepisy dotyczące narażenia na hałas w miejscu pracy, które są egzekwowane z różnym entuzjazmem. Wiele takich przepisów określa limit narażenia na ciągły hałas na poziomie 85 dB(A), dla 8-godzinnej zmiany. Za każde zwiększenie o 3 dB dopuszczalna ekspozycja zmniejsza się o połowę. Tak więc, jeśli pracujesz w klubie nocnym, gdzie wzmocniona muzyka wytwarza 100 dB(A) w pobliżu Twoich uszu, dopuszczalna ekspozycja wynosi 15 minut. Istnieje limit dla hałasu impulsowego, takiego jak broń palna lub narzędzia wykorzystujące strzały wybuchowe. (Istnieje wiele dokumentów zawierających porady, jak zmniejszyć narażenie na hałas u źródła (np. zmniejszyć poziom muzyki), między źródłem a uchem (np. odsunąć się od głośników na koncercie) oraz przy uchu (np. nosić zatyczki do uszu lub przemysłowe ochronniki słuchu). Zarządzanie hałasem i ochrona słuchu w miejscu pracy jest kodeksem postępowania w stanie Nowa Południowa Walia, Australia (adres autora).

Kilka najczęściej zadawanych pytań

• Jak głośny jest samolot? Pociąg? Osoba śpiewająca? Szczekający pies? Elektronarzędzie? Odpowiedzi na to pytanie różnią się znacznie. Zależy to w dużej mierze od tego, jak daleko się znajdujemy, czy jesteśmy w pomieszczeniu, czy nie, czy jest pogłos, jak silne jest dane źródło i jakie jest jego spektrum. Podawanie wartości, bez dokładnego określenia warunków, byłoby nieco mylące. Ponieważ reszta tej strony ma być wiarygodna, wolałbym nie podawać tutaj wartości.
• Jak się „dodaje decybele”, czyli jaki poziom dźwięku otrzymamy po dodaniu poziomu a do poziomu b? Jeśli źródła są spójne (co zwykle oznacza, że ostatecznie pochodzą z tego samego źródła), to mogą wystąpić skomplikowane efekty interferencyjne. W większości przypadków, gdy źródła są niezależne, można dodać natężenia, a następnie przeliczyć je na decybele. Jednakże, jeśli poziom dźwięku podany jest w dB(A), nie jest tak łatwo wrócić do natężenia i trzeba wiedzieć coś o widmie dźwięku. Jeśli znasz rozkład dźwięku w różnych pasmach częstotliwości, możesz użyć apletu na tym linku.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.