Przewaga komparatywna

admin

Adam Smith po raz pierwszy nawiązał do koncepcji przewagi absolutnej jako podstawy handlu międzynarodowego w 1776 r., w Bogactwie narodów:

Jeśli obcy kraj może dostarczyć nam towar taniej, niż my sami możemy go wyprodukować, lepiej odkupmy go od nich za część produkcji naszego własnego przemysłu zatrudnionego w sposób, w którym mamy pewną przewagę. Ogólny przemysł kraju, będący zawsze w proporcji do kapitału, który go zatrudnia, nie będzie przez to pomniejszony, lecz tylko pozostawiony, aby znaleźć sposób, w jaki może być zatrudniony z największą korzyścią.

Pisząc kilkadziesiąt lat po Smithie, w 1808 r. Robert Torrens sformułował wstępną definicję przewagi komparatywnej jako straty wynikającej z zamknięcia handlu:

Jeśli chcę poznać zakres korzyści, która wynika dla Anglii z tego, że dała ona Francji sto funtów sukna w zamian za sto funtów koronki, biorę ilość koronki, którą nabyła w wyniku tej transakcji, i porównuję ją z ilością, którą mogłaby, przy takim samym nakładzie pracy i kapitału, nabyć, wytwarzając ją u siebie. Koronki, które pozostały, poza tym, co praca i kapitał zatrudnione przy produkcji materiału, mogłyby wytworzyć w domu, to wielkość korzyści, jaką Anglia czerpie z wymiany.

David Ricardo

W 1817 r. w książce O zasadach ekonomii politycznej i opodatkowania David Ricardo opublikował to, co od tego czasu stało się znane jako teoria przewagi komparatywnej.

Przykład RicardoEdit

Wykres ilustrujący przykład Ricardo:
W przypadku I (romby) każdy kraj poświęca 3600 godzin na wyprodukowanie mieszanki tkaniny i wina.
W przypadku II (kwadraty), każdy kraj specjalizuje się w swojej przewadze komparatywnej, co skutkuje większą całkowitą produkcją.

W słynnym przykładzie Ricardo rozważa gospodarkę światową składającą się z dwóch krajów, Portugalii i Anglii, z których każdy produkuje dwa dobra o identycznej jakości. W Portugalii, kraju a priori bardziej wydajnym, możliwe jest wyprodukowanie wina i sukna przy mniejszym nakładzie pracy, niż byłoby to konieczne do wyprodukowania tych samych ilości w Anglii. Jednak koszty względne lub ranking kosztów produkcji tych dwóch dóbr różnią się między krajami.

Godziny pracy potrzebne do wyprodukowania jednej jednostki
Produce
Country
 Cloth Wine
England 100 120
Portugal 90 80

In this illustration, England could commit 100 hours of labor to produce one unit of cloth, or produce 5/6 units of wine. Meanwhile, in comparison, Portugal could commit 100 hours of labor to produce 10/9 units of cloth, or produce 10/8 units of wine. So, Portugal possesses an absolute advantage in producing cloth due to more produced per hour (since 10/9 > 1), but England has a comparative advantage in producing cloth due to lower opportunity cost.

Innymi słowy, jeśli dla danego kraju tańsze jest produkowanie jednego dobra w stosunku do drugiego, to będzie on miał przewagę komparatywną i zachętę do produkowania większej ilości tego dobra, które jest dla niego relatywnie tańsze do wyprodukowania niż drugie – zakładając, że ma korzystną możliwość handlu na rynku tym drugim, trudniejszym do wyprodukowania dobrem. Podobnie, każdy powinien skorzystać z okazji, by zaoferować na rynku dobro, które ma względną przewagę w produkcji.

W przypadku braku handlu, Anglia wymaga 220 godzin pracy, by wyprodukować i skonsumować po jednej jednostce sukna i wina, podczas gdy Portugalia wymaga 170 godzin pracy, by wyprodukować i skonsumować te same ilości. Anglia jest bardziej wydajna w produkcji sukna niż wina, a Portugalia jest bardziej wydajna w produkcji wina niż sukna. Jeśli więc każdy kraj wyspecjalizuje się w dobrach, w których ma przewagę komparatywną, to globalna produkcja obu dóbr wzrośnie, ponieważ Anglia może poświęcić 220 godzin pracy na wyprodukowanie 2,2 jednostki sukna, a Portugalia 170 godzin na wyprodukowanie 2,125 jednostki wina. Co więcej, jeśli oba kraje wyspecjalizują się w powyższy sposób i Anglia wymieni jedną jednostkę sukna na 5/6-9/8 jednostki wina portugalskiego, to oba kraje mogą skonsumować co najmniej po jednej jednostce sukna i wina, a w każdym z nich pozostanie od 0 do 0,2 jednostki sukna i od 0 do 0,125 jednostki wina do skonsumowania lub wyeksportowania. W konsekwencji, zarówno Anglia jak i Portugalia mogą konsumować więcej wina i tkanin w warunkach wolnego handlu niż w autarkii.

Model RicardianaEdit

Model Ricardiana jest matematycznym modelem równowagi ogólnej w handlu międzynarodowym. Chociaż idea modelu ricardiańskiego została po raz pierwszy przedstawiona w Essay on Profits (wersja jednoproduktowa), a następnie w Principles (wersja wieloproduktowa) przez Davida Ricardo, pierwszy matematyczny model ricardiański został opublikowany przez Williama Whewella w 1833 roku. Najwcześniejszy test modelu ricardiańskiego został przeprowadzony przez G.D.A MacDougalla, który został opublikowany w Economic Journal z 1951 i 1952 roku. W modelu ricardiańskim wzorce handlu zależą od różnic w produktywności.

Poniżej przedstawiono typową współczesną interpretację klasycznego modelu ricardiańskiego. Dla uproszczenia zastosowano w niej notację i definicje, takie jak koszt alternatywny, niedostępne dla Ricardo.

Gospodarka światowa składa się z dwóch krajów, rodzimego i obcego, które produkują wino i sukno. Praca, jedyny czynnik produkcji, jest mobilna w kraju, ale nie na arenie międzynarodowej; może występować migracja między sektorami, ale nie między krajami. Oznaczamy siłę roboczą w kraju macierzystym przez L {{displaystyle \textstyle L}}.

textstyle L

, ilość pracy potrzebnej do wyprodukowania jednej jednostki wina w kraju przez a L W {{displaystyle \textstyle a_{LW}}

textstyle a_{LW}}

, a ilość pracy potrzebnej do wyprodukowania jednej jednostki tkaniny w Home przez L C {displaystyle a_{LC}}

textstyle a_{LC}}

. Całkowita ilość wina i sukna wyprodukowanego w domu wynosi Q W {textstyle Q_{W}}

Q_{W}}

oraz Q C {{displaystyle Q_{C}}

Q_{C}

odpowiednio. Oznaczamy te same zmienne dla Foreign przez dodanie liczby pierwszej. Na przykład, a L W ′ {{displaystyle ′textstyle a’_{LW}}

textstyle a'_{LW}}'_{{LW}}

to ilość pracy potrzebna do wyprodukowania jednostki wina w Foreign.

Nie wiemy, czy Home może produkować tkaniny przy użyciu mniejszej liczby godzin pracy niż Foreign. To znaczy, nie wiemy, czy a L C < a L C ′ {{LC}<a’_{LC}}

a_{{LC}}a'_{LC}}'_{{LC}}

. Podobnie nie wiemy, czy Dom może produkować wino przy użyciu mniejszej liczby godzin pracy. Zakładamy jednak, że Dom jest relatywnie bardziej produktywny niż Zagranica w produkcji tkanin vs. wina: a L C / a L C ′ < a L W / a L W ′ . {\displaystyle a_{LC}/a’_{LC}<a_{LW}/a’_{LW}.}

a_{{LC}}/a'_{{LC}}a_{{LW}}/a'_{{LW}}.'_{{LC}}<a_{{LW}}/a'_{{LW}}.

Ekwiwalentnie, możemy założyć, że Home ma przewagę komparatywną w tkaninach w tym sensie, że ma niższy koszt alternatywny dla tkanin w kategoriach wina niż Foreign:

a L C / a L W < a L C ′ / a L W ′ . {\displaystyle a_{LC}/a_{LW}<a’_{LC}/a’_{LW}.}

a_{{LC}}/a_{LW}}a'_{LC}}/a'_{LW}}.'_{{LC}}/a'_{{LW}}.

W przypadku braku handlu względna cena sukna i wina w każdym kraju jest określana wyłącznie przez względny koszt pracy przy wytwarzaniu tych towarów. Stąd względna autarkiczna cena sukna wynosi a L C / a L W {{displaystyle a_{LC}/a_{LW}}.

a_{{LC}}/a_{LW}}

w domu oraz a L C ′ / a L W ′ {displaystyle a’_{LC}/a’_{LW}}

w Zagranicznych. Przy wolnym handlu cena sukna lub wina w którymkolwiek z krajów jest ceną światową P C {{C}}

P_{C}

lub P W {displaystyle P_{W}}

P_W

. amiast rozważać światowy popyt (lub podaż) na tkaniny i wino, interesuje nas światowy względny popyt (lub względna podaż) na tkaniny i wino, który definiujemy jako stosunek światowego popytu (lub podaży) na tkaniny do światowego popytu (lub podaży) na wino. In general equilibrium, the world relative price P C / P W {\displaystyle \textstyle P_{C}/P_{W}}

\textstyle P_{C}/P_{W}

will be determined uniquely by the intersection of world relative demand R D {\displaystyle \textstyle RD}

\textstyle RD

and world relative supply R S {\displaystyle \textstyle RS}

\textstyle RS

curves.

The demand for cloth relative to wine decreases with the relative price of cloth in terms of wine; the supply R S {\displaystyle RS}

RS

of cloth relative to wine increases with relative price. Two relative demand curves R D 1 {\displaystyle RD_{1}}

RD_{1}

and R D 2 {\displaystyle RD_{2}}

RD_{2}

zostały narysowane w celach poglądowych.

Zakładamy, że krzywa względnego popytu odzwierciedla efekty substytucji i jest malejąca względem ceny względnej. Zachowanie krzywej względnej podaży wymaga jednak bliższego zbadania. Przywołując nasze pierwotne założenie, że Dom ma przewagę komparatywną w tkaninach, rozważamy pięć możliwości względnej ilości dostarczanych tkanin przy danej cenie.

  • Jeśli P C / P W = a L C / a L W < a L C ′ / a L W ′ {{displaystyle P_{C}/P_{W}=a_{LC}/a_{LW}}<a’_{LC}/a’_{LW}}}
    textstyle P_{C}/P_{W}=a_{{LC}}/a_{LW}}/a'_{LC}}/a'_{LW}}'_{{LC}}/a'_{{LW}}

    , wówczas Foreign specjalizuje się w winie, dla płacy P W ′ / a L W ′ {{displaystyle P’_{W}/a’_{LW}}.

    P'_{W}/a'_{LW}}'_{W}/a'_{{LW}}

    w sektorze winiarskim jest większa niż płaca P C ′ / a L C ′ {displaystyle P’_{C}/a’_{LC}}

    P'_{C}/a'_{{LC}}'_{C}/a'_{{LC}}

    in the cloth sector. However, Home workers are indifferent between working in either sector. As a result, the quantity of cloth supplied can take any value.

  • If P C / P W < a L C / a L W < a L C ′ / a L W ′ {\displaystyle \textstyle P_{C}/P_{W}<a_{LC}/a_{LW}<a’_{LC}/a’_{LW}}
    \textstyle P_{C}/P_{W}a_{{LC}}/a_{{LW}}a'_{{LC}}/a'_{{LW}}'_{{LC}}/a'_{{LW}}

    , then both Home and Foreign specialize in wine, for similar reasons as above, and so the quantity of cloth supplied is zero.

  • If a L C / a L W < P C / P W < a L C ′ / a L W ′ {\displaystyle \textstyle a_{LC}/a_{LW}<P_{C}/P_{W}<a’_{LC}/a’_{LW}}
    textstyle a_{{LC}}/a_{LW}}P_{C}/P_{W}}a'_{LC}}/a'_{LW}}'_{{LC}}/a'_{{LW}}

    , wówczas Home specjalizuje się w tkaninach, podczas gdy Foreign specjalizuje się w winie. Ilość dostarczanych tkanin jest dana stosunkiem L / a L C L ′ / a L W ′ {{displaystyle }textstyle {{frac {L/a_{LC}}}{L’/a’_{LW}}}}}}

    textstyle {displayplaystyle {{L/a_{LC}}}{L'/a'_{LW}}}}'/a'_{{LW}}}}

    światowej produkcji tkanin do światowej produkcji wina.

  • Jeżeli a L C / a L W < a L C ′ / a L W ′ < P C / P W. {{displaystyle}}textstyle a_{LC}/a_{LW}<a’_{LC}/a’_{LW}<P_{C}/P_{W}}
    tekstylia a_{LC}}/a_{LW}}a'_{LC}/a'_{LW}}}P_{C}/P_{W}'_{{LC}}/a'_{{LW}}<P_{C}/P_{W}

    , wówczas zarówno kraj jak i zagranica specjalizują się w tkaninach. Ilość dostarczanych tkanin dąży do nieskończoności, a ilość dostarczanego wina zbliża się do zera.

  • Jeżeli a L C / a L W < a L C ′ / a L W ′ = P C / P W {tekstylia a_{LC}/a_{LW}<a’_{LC}/a’_{LW}=P_{C}/P_{W}}}
    \textstyle a_{{LC}}/a_{{LW}}<a'_{{LC}}/a'_{{LW}}=P_{C}/P_{W} a_{LC}}/a_{LW}}a’_{LC}}/a’_{LW}}=P_{C}/P_{W}

    , wówczas pracownicy krajowi specjalizują się w produkcji tkanin, podczas gdy pracownicy zagraniczni są obojętni między sektorami. Ponownie, względna ilość dostarczanych tkanin może przyjąć dowolną wartość.

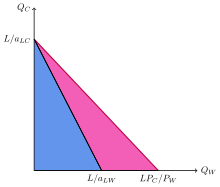
Niebieski trójkąt przedstawia pierwotne możliwości produkcyjne (i konsumpcyjne) Domu. Poprzez handel, Home może również konsumować pakiety w różowym trójkącie, mimo że stoi przed tą samą granicą możliwości produkcyjnych.

Dopóki względny popyt jest skończony, względna cena jest zawsze ograniczona nierównością

a L C / a L W ≤ P C / P W ≤ a L C ′ / a L W ′ . {{displaystyle a_{LC}/a_{LW}} {{P_{C}/P_{W}} {{a’_{LC}/a’_{LW}}}.}

a_{{LC}}/a_{LW}}leq {P_{C}/P_{W}}} {a'_{LC}}/a'_{LW}}}.'_{{LC}}/a'_{{LW}}}.

W autarkii Home napotyka ograniczenie produkcyjne postaci

a L C Q C + a L W Q W ≤ L , {{displaystyle a_{LC}Q_{C}+a_{LW}Q_{W}}leq L,}

a_{LC}}Q_{C}+a_{{LW}Q_{W}}leq L,

Z czego wynika, że konsumpcja tkanin przez dom na granicy możliwości produkcyjnych wynosi

Q C = L / a L C – ( a L W / a L C ) Q W {{C}=L/a_{LC}-(a_{LW}/a_{LC})Q_{W}}.

Q_{C}=L/a_{{LC}}-(a_{{LW}}/a_{{LC}})Q_{W}

.

Przy wolnym handlu gospodarstwo domowe produkuje wyłącznie sukno, którego pewną ilość eksportuje w zamian za wino po obowiązującym kursie. Zatem całkowita konsumpcja w gospodarstwie domowym podlega teraz ograniczeniu

a L C Q C + a L C ( P W / P C ) Q W ≤ L {{displaystyle a_{LC}Q_{C}+a_{LC}(P_{W}/P_{C})Q_{W}} „3.3.1.”).

a_{{LC}}Q_{C}+a_{LC}}(P_{W}/P_{C})Q_{W}}leq L

podczas gdy jego konsumpcja tkanin na granicy możliwości konsumpcyjnych jest dana przez możliwości konsumpcyjnych jest dana przez

Q C = L / a L C – ( P W / P C ) Q W ≥ L / a L C – ( a L W / a L C ) Q W {styl Q_{C}=L/a_{LC}-(P_{W}/P_{C})Q_{W}\geq L/a_{LC}-(a_{LW}/a_{LC})Q_{W}}

Q_{C}=L/a_{{LC}}-(P_{W}/P_{C})Q_{W}\geq L/a_{{LC}}-(a_{{LW}}/a_{{LC}})Q_{W}

.

Symetryczny argument dotyczy Zagranicy. Dlatego, handlując i specjalizując się w dobrach, w których ma przewagę komparatywną, każdy kraj może rozszerzyć swoje możliwości konsumpcyjne. Konsumenci mogą wybierać spośród pakietów wina i tkanin, których nie mogliby sami wyprodukować w gospodarkach zamkniętych.

Istnieje inny sposób udowodnienia teorii przewagi komparatywnej, który wymaga mniej założeń niż powyższy szczegółowy dowód, a w szczególności nie wymaga, aby płace godzinowe były równe w obu branżach, ani nie wymaga równowagi między ofertą a popytem na rynku. Taki dowód może być rozszerzony na sytuacje z wieloma dobrami i wieloma krajami, niezmiennymi zwrotami i więcej niż jednym czynnikiem produkcji.

Warunki handluEdit

Warunki handlu to stopa, po której jedno dobro może być wymieniane na inne. Jeśli oba kraje specjalizują się w dobrach, dla których mają przewagę komparatywną, to handel, warunki handlu dla dobra (które przynoszą korzyści obu podmiotom) wypadną pomiędzy kosztami alternatywnymi każdego podmiotu. W powyższym przykładzie jedna jednostka tkaniny będzie sprzedawana za 5 6 {displaystyle {frac {5}{6}}}.

{{{frac 56}

jednostkami wina i 9 8 {{displaystyle {{frac {9}{8}}}} jednostkami wina.

{frac 98}

jednostek wina.