Rodzaje interpolacji – zalety i wady
Metody interpolacji
Interpolacja to proces wykorzystywania punktów o znanych wartościach lub punktów próbnych do szacowania wartości w innych nieznanych punktach. Może być stosowana do przewidywania nieznanych wartości dla dowolnych geograficznych danych punktowych, takich jak wysokość, opady, stężenia chemiczne, poziomy hałasu i tak dalej.
Dostępne metody interpolacji są wymienione poniżej.
Inverse Distance Weighted (IDW)
Inverse Distance Weighting interpolator zakłada, że każdy punkt wejściowy ma lokalny wpływ, który maleje wraz z odległością. Punkty znajdujące się bliżej komórki przetwarzającej mają większą wagę niż te znajdujące się dalej. Do określenia wartości wyjściowej dla każdej lokalizacji można użyć określonej liczby punktów lub wszystkich punktów w określonym promieniu. Zastosowanie tej metody zakłada, że wpływ mapowanej zmiennej maleje wraz z odległością od miejsca jej próbkowania.
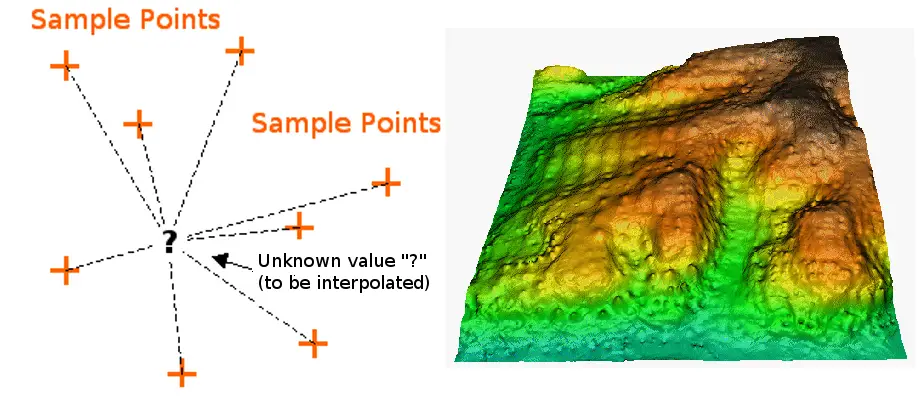
IDW Interpolation; Dzięki uprzejmości: QGIS
Algorytm Inverse Distance Weighting (IDW) efektywnie jest interpolatorem średniej ruchomej, który jest zwykle stosowany do danych o dużej zmienności. W przypadku niektórych typów danych możliwy jest powrót do miejsca gromadzenia danych i zarejestrowanie nowej wartości, która statystycznie różni się od pierwotnego odczytu, ale mieści się w ogólnym trendzie dla danego obszaru.
Powierzchnia interpolowana, oszacowana przy użyciu techniki średniej ruchomej, jest mniejsza niż lokalna wartość maksymalna i większa niż lokalna wartość minimalna.

IDW Interpolated Surface; Dzięki uprzejmości:ESRI
InterpolacjaIDW wyraźnie realizuje założenie, że rzeczy, które są blisko siebie, są bardziej podobne niż te, które są dalej od siebie. Aby przewidzieć wartość dla dowolnej niepomierzonej lokalizacji, IDW użyje zmierzonych wartości otaczających lokalizację przewidywania. Te zmierzone wartości, które znajdują się najbliżej przewidywanej lokalizacji, będą miały większy wpływ na przewidywaną wartość niż te bardziej oddalone. Zatem IDW zakłada, że każdy zmierzony punkt ma lokalny wpływ, który maleje wraz z odległością. Funkcję IDW należy stosować, gdy zbiór punktów jest wystarczająco gęsty, aby uchwycić zakres lokalnej zmienności powierzchni potrzebnej do analizy. IDW wyznacza wartości komórek przy użyciu liniowo ważonego zestawu kombinacji punktów próbnych. Punkty położone bliżej miejsca predykcji mają większą wagę niż te położone dalej, stąd nazwa inverse distance weighted.
Technika IDW oblicza wartość dla każdego węzła siatki poprzez badanie otaczających punktów danych, które leżą w promieniu wyszukiwania zdefiniowanym przez użytkownika. Niektóre lub wszystkie punkty danych mogą być użyte w procesie interpolacji. Wartość węzła jest obliczana poprzez uśrednienie sumy ważonej wszystkich punktów. Punkty danych leżące stopniowo dalej od węzła mają znacznie mniejszy wpływ na obliczoną wartość niż te leżące bliżej węzła.
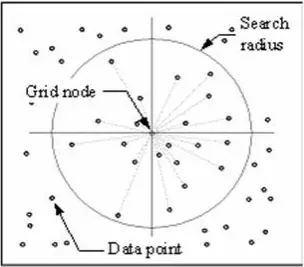
Wokół każdego węzła siatki generowany jest promień, z którego wybierane są punkty danych do wykorzystania w obliczeniach. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Inna metoda średniej ważonej, podstawowe równanie używane w interpolacji naturalnego sąsiada jest identyczne z tym używanym w interpolacji IDW. Metoda ta może skutecznie obsługiwać duże wejściowe zbiory danych punktów. Podczas korzystania z metody Natural Neighbor, lokalne współrzędne określają wielkość wpływu dowolnego punktu rozproszenia na komórki wyjściowe.
Metoda Natural Neighbour jest geometryczną techniką estymacji, która wykorzystuje naturalne regiony sąsiedztwa wygenerowane wokół każdego punktu w zbiorze danych.
Podobnie jak IDW, ta metoda interpolacji jest metodą interpolacji średniej ważonej. Jednak zamiast znajdować wartość interpolowanego punktu przy użyciu wszystkich punktów wejściowych ważonych przez ich odległość, interpolacja Natural Neighbors tworzy triangulację Delauneya punktów wejściowych i wybiera najbliższe węzły, które tworzą wypukły kadłub wokół punktu interpolacji, a następnie waży ich wartości przez proporcjonalny obszar. Metoda ta jest najbardziej odpowiednia w przypadku, gdy przykładowe punkty danych są rozmieszczone z nierówną gęstością. Jest to dobra technika interpolacji ogólnego przeznaczenia i ma tę zaletę, że nie trzeba określać parametrów, takich jak promień, liczba sąsiadów czy wagi.

Natural IDW: Dzięki uprzejmości: ESRI
Ta technika jest przeznaczona do honorowania lokalnych wartości minimalnych i maksymalnych w pliku punktów i może być ustawiona tak, aby ograniczyć overshoots lokalnych wysokich wartości i undershoots lokalnych niskich wartości. W ten sposób metoda pozwala na tworzenie dokładnych modeli powierzchni ze zbiorów danych, które są bardzo słabo rozłożone lub bardzo liniowe w rozkładzie przestrzennym.
Zalety
- Obsługuje duże liczby punktów próbnych wydajnie.
Spline
Spline szacuje wartości za pomocą funkcji matematycznej, która minimalizuje ogólną krzywiznę powierzchni, dając w rezultacie gładką powierzchnię, która przechodzi dokładnie przez punkty wejściowe.

Spline: Courtesy: ESRI
Koncepcyjnie jest to analogiczne do zginania arkusza gumy, aby przejść przez znane punkty, jednocześnie minimalizując całkowitą krzywiznę powierzchni. Dopasowuje funkcję matematyczną do określonej liczby najbliższych punktów wejściowych, jednocześnie przechodząc przez punkty próbne. Metoda ta jest najlepsza dla łagodnie zmieniających się powierzchni, takich jak wzniesienia, wysokości zwierciadła wody lub stężenia zanieczyszczeń.
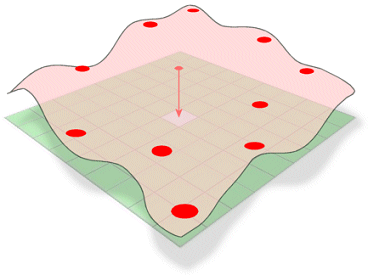
Metoda interpolacji Spline szacuje nieznane wartości poprzez zginanie powierzchni przez znane wartości.
Istnieją dwie metody spline: regularized i tension.
Metoda regularized tworzy gładką, stopniowo zmieniającą się powierzchnię z wartościami, które mogą leżeć poza zakresem danych próbki. Włącza pierwszą pochodną (nachylenie), drugą pochodną (szybkość zmiany nachylenia) i trzecią pochodną (szybkość zmiany drugiej pochodnej) do swoich obliczeń minimalizacyjnych.
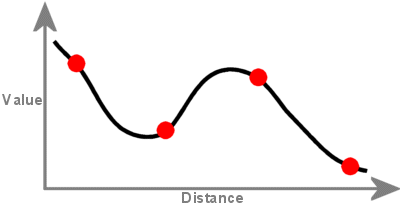
Powierzchnia utworzona za pomocą interpolacji Spline przechodzi przez każdy punkt próbkowania i może przekroczyć zakres wartości zestawu punktów próbkowania.
Aczkolwiek splajn Tension wykorzystuje tylko pierwszą i drugą pochodną, uwzględnia więcej punktów w obliczeniach Spline, co zazwyczaj tworzy gładsze powierzchnie, ale zwiększa czas obliczeń.
Ta metoda przeciąga powierzchnię nad pozyskanymi punktami dając efekt rozciągnięcia. Spline wykorzystuje zakrzywione linie (metoda Curvilinear Lines) do obliczania wartości komórek.
Wybór wagi dla interpolacji Spline
Regularized spline: Im większa waga, tym gładsza powierzchnia. Odpowiednie są wagi z przedziału od 0 do 5. Typowe wartości to 0, .001, .01, .1, i .5.
Splajn napinający: Im wyższa waga, tym grubsza powierzchnia i bardziej wartości są zgodne z zakresem przykładowych danych. Wartości wagowe muszą być większe lub równe zeru. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Kriging procedura, która generuje oszacowaną powierzchnię z rozproszonego zbioru punktów z wartościami z. Kriging zakłada, że odległość lub kierunek pomiędzy punktami próby odzwierciedla korelację przestrzenną, która może być wykorzystana do wyjaśnienia zmienności powierzchni. Narzędzie Kriging dopasowuje funkcję matematyczną do określonej liczby punktów lub wszystkich punktów w określonym promieniu, aby określić wartość wyjściową dla każdej lokalizacji. Kriging jest procesem wieloetapowym; obejmuje eksploracyjną analizę statystyczną danych, modelowanie wariogramu, tworzenie powierzchni i (opcjonalnie) badanie powierzchni wariancji. Kriging jest najbardziej odpowiedni, gdy wiadomo, że dane są przestrzennie skorelowane z odległością lub kierunkiem. Jest on często stosowany w gleboznawstwie i geologii.
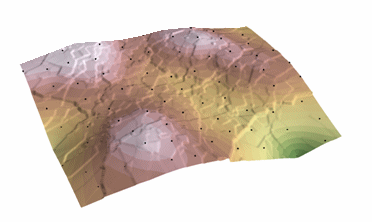
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
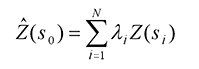
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Jednak w metodzie krigingu wagi opierają się nie tylko na odległości między zmierzonymi punktami a lokalizacją predykcji, ale także na ogólnym układzie przestrzennym zmierzonych punktów. Aby wykorzystać układ przestrzenny w wagach, należy określić ilościowo autokorelację przestrzenną. Tak więc w zwykłym krigingu waga, λi, zależy od dopasowanego modelu do mierzonych punktów, odległości do miejsca przewidywania oraz relacji przestrzennych między mierzonymi wartościami wokół miejsca przewidywania. W kolejnych rozdziałach omówiono sposób wykorzystania ogólnej formuły krigingu do utworzenia mapy powierzchni predykcji oraz mapy dokładności predykcji.
Typy krigingu
Kriging ordynarny
Kriging ordynarny zakłada model
Z(s) = µ + ε(s),
gdzie µ jest nieznaną stałą. Jednym z głównych problemów dotyczących zwykłego krigingu jest to, czy założenie stałej średniej jest uzasadnione. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indicator Kriging
Indicator kriging zakłada model
I(s) = µ + ε(s),
gdzie µ jest nieznaną stałą, a I(s) jest zmienną binarną. Tworzenie danych binarnych może odbywać się poprzez zastosowanie progu dla danych ciągłych lub może być tak, że obserwowane dane mają wartość 0 lub 1. Na przykład, można mieć próbę, która składa się z informacji o tym, czy punkt jest siedliskiem leśnym czy nieleśnym, gdzie zmienna binarna wskazuje przynależność do klasy. Używając zmiennych binarnych, kriging wskaźnikowy przebiega tak samo jak kriging zwykły.
Kriging wskaźnikowy może używać semiwariogramów lub kowariancji.
Probability Kriging
Probability kriging zakłada model
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
gdzie µ1 i µ2 są nieznanymi stałymi, a I(s) jest zmienną binarną utworzoną przez użycie wskaźnika progowego, I(Z(s) > ct). Zauważmy, że teraz istnieją dwa rodzaje błędów losowych, ε1(s) i ε2(s), więc istnieje autokorelacja dla każdego z nich i korelacja krzyżowa między nimi. Probability kriging stara się robić to samo, co kriging wskaźnikowy, ale używa cokrigingu, próbując wykonać lepszą pracę.
Kriging prawdopodobieństwa może wykorzystywać semiwariogramy lub kowariancje, kowariancje krzyżowe i transformacje, ale nie może uwzględniać błędu pomiaru.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-.slot=”9271753327″>
Disjunctive Kriging
Disjunctive kriging zakłada, że. model
f(Z(s)) = µ1 + ε(s),
gdzie µ1 jest nieznaną stałą, a f(Z(s)) jest dowolną funkcją Z(s). Zauważ, że możesz napisać f(Z(s)) = I(Z(s) > ct), więc kriging wskaźnikowy jest szczególnym przypadkiem krigingu dysjunktywnego. W programie Geostatistical Analyst można przewidywać albo samą wartość, albo wskaźnik za pomocą krigingu disjunktywnego.
Ogólnie rzecz biorąc, disjunctive kriging stara się zrobić więcej niż zwykły kriging. Podczas gdy nagrody mogą być większe, są też koszty. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Aby uzyskać głęboki wgląd w matematyczne podejście do metody Kriging, proszę kliknąć Kriging a Interpolation Method.
PointInterp
Metoda podobna do IDW, funkcja PointInterp pozwala na większą kontrolę nad sąsiedztwem próbkowania. Wpływ danej próbki na wartość interpolowanej komórki siatki zależy od tego, czy punkt próbki znajduje się w sąsiedztwie komórki i jak daleko od interpolowanej komórki jest położony. Punkty poza sąsiedztwem nie mają żadnego wpływu.

PointInterp; Courtesy: ESRI
Wartość ważona punktów wewnątrz sąsiedztwa jest obliczana przy użyciu odwrotnej interpolacji ważonej odległością lub odwrotnej wykładniczej interpolacji odległości. Metoda ta interpoluje raster przy użyciu cech punktowych, ale pozwala na różne typy sąsiedztwa. Sąsiedztwa mogą mieć kształty takie jak okręgi, prostokąty, nieregularne wielokąty, annulusy lub kliny.
Trend
Trend jest metodą statystyczną, która znajduje powierzchnię pasującą do przykładowych punktów za pomocą dopasowania regresji najmniejszych kwadratów. Dopasowuje ona jedno równanie wielomianowe do całej powierzchni. Dzięki temu uzyskuje się powierzchnię, która minimalizuje wariancję powierzchni w stosunku do wartości wejściowych. Powierzchnia jest tak skonstruowana, że dla każdego punktu wejściowego, suma różnic pomiędzy wartościami rzeczywistymi a wartościami oszacowanymi (tj. wariancja) będzie tak mała, jak to tylko możliwe.

Trend; Courtsey:ESRI
Jest to interpolator niedokładny, a wynikowa powierzchnia rzadko przechodzi przez punkty wejściowe. Jednak ta metoda wykrywa trendy w przykładowych danych i jest podobna do naturalnych zjawisk, które zazwyczaj zmieniają się płynnie.
Zalety
- Powierzchnie trendów są dobre do identyfikacji gruboskalowych wzorców w danych; interpolowana powierzchnia rzadko przechodzi przez punkty próbki.
Topo to Raster
Poprzez interpolację wartości wysokości dla rastra, metoda Topo to Raster nakłada ograniczenia, które zapewniają hydrologicznie poprawny cyfrowy model wysokości, który zawiera połączoną strukturę drenażu i prawidłowo reprezentuje grzbiety i strumienie z wejściowych danych konturowych. Wykorzystuje ona iteracyjną technikę interpolacji różnic skończonych, która optymalizuje wydajność obliczeniową interpolacji lokalnej bez utraty ciągłości powierzchniowej interpolacji globalnej. Został on specjalnie zaprojektowany do inteligentnej pracy z danymi wejściowymi konturu.
Poniżej znajduje się przykład powierzchni interpolowanej z punktów wysokościowych, linii konturowych, linii strumieni i wielokątów jeziora przy użyciu interpolacji Topo to Raster.
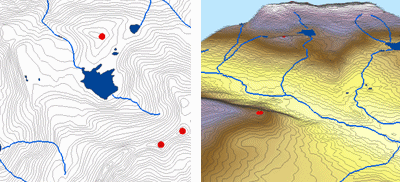
Topo do rastra; Dzięki uprzejmości: ESRI
Topo to Raster jest specjalistycznym narzędziem do tworzenia hydrologicznie poprawnych powierzchni rastrowych z danych wektorowych elementów terenu takich jak punkty wysokościowe, linie konturowe, linie strumieni, poligony jezior, punkty zlewowe oraz poligony granic obszaru opracowania.
Gęstość
Narzędzia gęstości (dostępne w ArcGIS) tworzą powierzchnię, która przedstawia jak dużo lub jak wiele jakiejś rzeczy jest na jednostce powierzchni. Narzędzie gęstości jest przydatne do tworzenia powierzchni gęstości w celu przedstawienia rozmieszczenia populacji dzikich zwierząt na podstawie zestawu obserwacji lub stopnia urbanizacji obszaru na podstawie gęstości dróg.

Density Raster; Courtest: ERSI
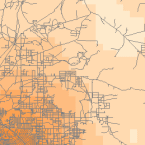
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method