Rozkład krańcowy

Rozkłady prawdopodobieństwa > Rozkład krańcowy

Co to jest rozkład krańcowy?

Zobacz film lub przeczytaj artykuł poniżej:

Definicja techniczna może być nieco przytłaczająca umysłowo:

Definicja rozkładu krańcowego = Jeśli X i Y są dyskretnymi zmiennymi losowymi, a f (x,y) jest wartością
ich wspólnego rozkładu prawdopodobieństwa w (x,y), to funkcje dane przez:
g(x) = Σy f (x,y) oraz h(y) = Σx f (x,y) są rozkładami krańcowymi odpowiednio X i Y .

Jeśli jesteś świetny z równaniami, to prawdopodobnie wszystko, co musisz wiedzieć. To mówi ci, jak znaleźć rozkład krańcowy. Ale jeśli ta formuła przyprawia cię o ból głowy (co robi większość ludzi!), możesz użyć tabeli rozkładu częstości, aby znaleźć rozkład krańcowy.

Rozkład krańcowy dostaje swoją nazwę, ponieważ pojawia się na marginesach tabeli rozkładu prawdopodobieństwa.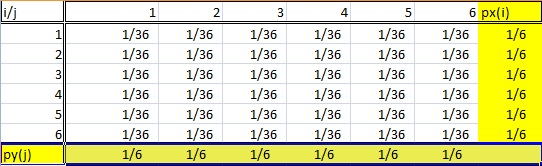

Oczywiście, to nie jest takie proste. Nie można po prostu spojrzeć na dowolną starą tabelę rozkładu częstości i powiedzieć, że ostatnia kolumna (lub wiersz) jest „rozkładem marginalnym”. Rozkłady brzegowe podlegają kilku regułom:

• Rozkład musi pochodzić z danych dwudzielnych. W powyższej tabeli, zmienne losowe i oraz j pochodzą z rzutu dwiema kostkami do gry.
• Rozkład marginalny to taki, w którym interesuje nas tylko jedna ze zmiennych losowych. Innymi słowy, albo X albo Y. Jeśli spojrzysz na tabelę prawdopodobieństwa powyżej, suma prawdopodobieństw jednej zmiennej jest wymieniona w dolnym rzędzie, a inne sumy prawdopodobieństw są wymienione w prawej kolumnie. Więc ta tabela ma dwa rozkłady krańcowe.

Różnica między rozkładem krańcowym a warunkowym.

Rozkład warunkowy jest wtedy, gdy jesteśmy zainteresowani tylko w określonej subpopulacji naszego całego zestawu danych. W przykładzie z toczeniem kostki, może to być „toczenie dwójki” lub „toczenie szóstki”. Poniższy obrazek przedstawia dwie wyróżnione subpopulacje (a zatem dwa rozkłady warunkowe).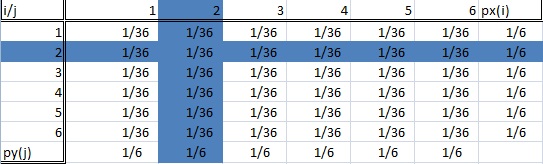

Jak obliczyć prawdopodobieństwo rozkładu marginalnego

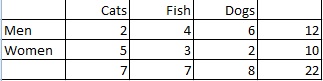
Przykładowe pytanie: Oblicz rozkład krańcowy preferencji zwierząt domowych wśród kobiet i mężczyzn:
Rozwiązanie:
Krok 1: Policz całkowitą liczbę osób. W tym przypadku całkowita liczba jest podana w prawej kolumnie (22 osoby).
Krok 2: Policz liczbę osób, które preferują każdy rodzaj zwierząt domowych, a następnie przekształć stosunek w prawdopodobieństwo:
Ludzie, którzy preferują koty: 7/22 = .32
Ludzie, którzy preferują ryby: 7/22 = .32
Ludzie, którzy preferują psy: 8/22 = .36
Porada: Możesz sprawdzić swoją odpowiedź, upewniając się, że wszystkie prawdopodobieństwa sumują się do 1.

Pytanie przykładowe nr 2 (Zdarzenia wzajemnie wykluczające się): Jeśli P(A) = 0,20, P(b) = 0,70, a oba zdarzenia wzajemnie się wykluczają, znajdź P(B’∩A), P(B’∩A’) i P(B∩A’).
Jeśli nie znasz tej notacji, P(A’) oznacza „nie A”, lub dopełnienie. P(B’∩A) oznacza „przecięcie nie B i A”).

Odpowiedź:
Możesz obliczyć prawdopodobieństwa indywidualnie, ale o wiele łatwiej jest je obliczyć używając tabeli.

Krok 1: Wypełnij tabelę częstości podanymi informacjami. Całkowite prawdopodobieństwo musi być równe 1, więc możesz dodać je do marginesów (sum). Proste dodawanie/algebra wypełnia marginalne puste miejsca. Na przykład, w dolnym rzędzie 0,70 + x = 1,00 więc suma krańcowa dla B’ musi wynosić 0,30.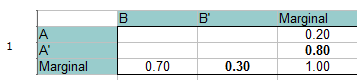

Krok 2: Dodaj 0 dla przecięcia A i B, w lewym górnym rogu tabeli. Możesz to zrobić, ponieważ A i B wzajemnie się wykluczają i nie mogą wystąpić razem.

Krok 3: Wypełnij pozostałe puste miejsca, używając prostego dodawania/algebry.

Czytając z tabeli (spójrz na przecięcia dwóch podanych prawdopodobieństw):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.

Przykładowe pytanie 3 (Zdarzenia niezależne): Jeśli P(A) = 0,20, P(b) = 0,70, a oba zdarzenia są niezależne, to znajdź P(B’∩A), P(B’∩A’) i P(B∩A’).

Odpowiedź: Tym razem A i B są niezależne, więc prawdopodobieństwo, że oba wystąpią jednocześnie wynosi 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Tę wartość wpisujemy w lewym górnym rogu (przecięcie A i B). Resztę tabeli wypełnij dokładnie tak samo, jak w krokach powyżej.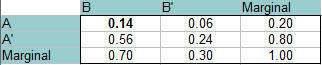

Odczytaj odpowiedzi z tabeli (z przecięć dwóch prawdopodobieństw):
P(B’∩A): 0.06
P(B’∩A’): 0.24
P(B∩A’): 0.56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, s. 536 i 571, 2002.
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

—————————————————————————–

Potrzebujesz pomocy w rozwiązaniu zadania domowego lub testu? Dzięki usłudze Chegg Study możesz uzyskać rozwiązanie swoich pytań krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!