Solving the Königsberg Bridge Problem

This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)

The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem

Have a look at the map above.

It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.

A map of the city is below. Możesz spojrzeć na oba diagramy – oba zawierają kluczowe informacje: które plamy ziemi są połączone z którymi innymi plamami ziemi i iloma mostami.

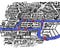
W języku technicznym przedstawiamy to jako graf. Plamy ziemi to wierzchołki, a mosty to krawędzie. Ale to nie jest ważne.

Problem polega na tym, czy możliwe jest znalezienie trasy, która przechodzi przez każdy most dokładnie raz. Oznacza to, że w naszym spacerze po mieście chcemy, aby nasza trasa przechodziła przez każdy most, ale nie może przechodzić przez niego dwa razy, ani trzy razy… Zasadniczo, jeśli znajdziesz się na tym samym moście, na którym byłeś wcześniej, ścieżka jest nieważna. Jeśli skończysz swoją wędrówkę i pojawi się most, przez który nie przeszedłeś, to twoja trasa była nieważna.

Rozwiązanie

Rozważmy każdy płat ziemi. Każdy most jest połączony z dwoma plamami ziemi (tak działają mosty). Tak się składa, że każdy płat ziemi ma nieparzystą liczbę mostów.

Zastanówmy się teraz, jak wyglądałby prawidłowy spacer.

Podczas spaceru zapisujesz w notatniku za każdym razem, gdy znajdujesz się w danym płacie ziemi. Na przykład, jeśli zaczniesz na najbardziej południowym krańcu miasta, zanotujesz to (zrobisz zdjęcie, kupisz pamiątkę…) i jeśli znajdziesz się tam ponownie, zwiększasz liczbę dla sektora południowego do dwóch.

Dla każdej plamy ziemi istnieją dwa przypadki

(1) jest to część miasta, w której nie zaczynamy spaceru, ani nie kończymy spaceru

(2) jest to część miasta, w której albo zaczynamy spacer, albo kończymy spacer, albo jedno i drugie.

Jasno widać, że istnieją co najwyżej 2 części miasta drugiego typu. Nie możemy zacząć w dwóch miejscach naraz, ani skończyć w dwóch miejscach naraz.

Jako że są cztery sekcje miasta, oznacza to, że są co najmniej dwie sekcje miasta, w których nie kończymy ani nie zaczynamy naszego spaceru. Wybierzmy jedną z nich.

Gdy wchodzimy do tego sektora, zużywamy jeden most, a gdy go opuszczamy, zużywamy drugi. Ale każdy sektor ma nieparzystą liczbę mostów! To jest sprzeczność. Aby zrozumieć dlaczego, przypomnijmy, że każdy sektor ma albo 3 mosty, albo 5 mostów.

Jeżeli jesteśmy w sektorze raz, możemy użyć tylko dwóch z jego mostów. Jeśli znajdziemy się w nim dwa razy, zużyjemy cztery z jego mostów (lub zabraknie nam mostów, jeśli ma tylko trzy mosty). Jeśli będziemy w nim trzy razy, będziemy potrzebowali 6 mostów, których nie możemy mieć. Zatem wymóg, byśmy zarówno wchodzili, jak i wychodzili z sektora miasta, który nie jest naszym punktem początkowym lub końcowym, jest sprzeczny z faktem, że liczba mostów łączących każdy sektor jest nieparzysta.

.