Theoretical Probability versus Experimental Probability
Słyszałeś terminy, teoretyczne prawdopodobieństwo i eksperymentalne prawdopodobieństwo, ale co one znaczą?
Czy są one w jakikolwiek sposób powiązane? To jest to, co zamierzamy odkryć w tej lekcji.
Jeśli ukończyłeś lekcje o niezależnym i zależnym prawdopodobieństwie, to już znalazłeś teoretyczne prawdopodobieństwo dla wielu problemów.
Prawdopodobieństwo teoretyczne
Prawdopodobieństwo teoretyczne jest prawdopodobieństwem, które jest obliczane przy użyciu wzorów matematycznych. Jest to prawdopodobieństwo oparte na teorii matematycznej.
Prawdopodobieństwo doświadczalne
Prawdopodobieństwo doświadczalne jest obliczane, gdy rzeczywista sytuacja lub problem jest wykonywany jako eksperyment. W tym przypadku przeprowadzasz eksperyment i używasz rzeczywistych wyników do określenia prawdopodobieństwa.
Aby dokładnie przeprowadzić eksperyment, musisz:
- Zidentyfikować, co stanowi „próbę”.
- Przeprowadzić minimum 25 prób
- Ustawić organizator (tabelę lub wykres), aby zapisać swoje dane.
Przyjrzyjrzyjmy się przykładowi, w którym najpierw obliczamy prawdopodobieństwo teoretyczne, a następnie przeprowadzamy eksperyment, aby określić prawdopodobieństwo doświadczalne.
Ciekawe będzie porównanie prawdopodobieństwa teoretycznego i prawdopodobieństwa doświadczalnego. Czy uważasz, że oba obliczenia będą zbliżone?
Przykład 1 – Teoretyczne Versus Doświadczalne
Ten problem pochodzi z Przykładu 1 z lekcji o zdarzeniach niezależnych. Obliczyliśmy, że teoretyczne prawdopodobieństwo wynosi 1/12 lub 8,3%. Przyjrzyjmy się:
Prawdopodobieństwo teoretyczne

Ponieważ wiemy, że prawdopodobieństwo teoretyczne wynosi 8.3% szansy na odwrócenie głowy i wyrzucenie szóstki, zobaczmy co się stanie, gdy faktycznie przeprowadzimy eksperyment.
Prawdopodobieństwo eksperymentalne
Zidentyfikuj próbę: Próba polega na jednokrotnym rzucie monetą i jednokrotnym rzuceniu kością.
Przeprowadź 25 prób i zapisz dane w poniższej tabeli.
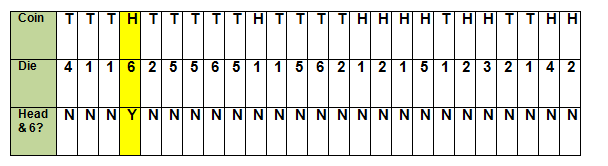
W każdej próbie raz rzuciłem monetą i raz rzuciłem kością. Zapisałem H dla głów i T dla reszek w wierszu oznaczonym „Moneta.”
Zapisałem liczbę na kostce w wierszu oznaczonym „Kość”.
W ostatnim wierszu określiłem, czy próba zakończyła się wydarzeniem rzucenia głowy i rzucenia szóstki.
W tym eksperymencie była tylko 1 próba (z 25), w której na monecie wypadł orzeł, a na kości wypadła szóstka.
To oznacza, że prawdopodobieństwo eksperymentu wynosi 1/25 lub 4%.
Wskazówka
Proszę zauważyć, że eksperyment każdego człowieka będzie inny; co pozwala na zróżnicowanie prawdopodobieństwa eksperymentalnego.
Również, im więcej prób przeprowadzisz w swoim eksperymencie, tym bardziej zbliżone będą twoje obliczenia dla prawdopodobieństwa doświadczalnego i teoretycznego.
Wnioski
Prawdopodobieństwo teoretyczne wynosi 8,3%, a prawdopodobieństwo doświadczalne 4%. Chociaż prawdopodobieństwo doświadczalne jest nieco niższe, nie jest to znacząca różnica.
W większości doświadczeń prawdopodobieństwo teoretyczne i doświadczalne nie będą sobie równe; powinny być jednak stosunkowo bliskie.
If the calculations are not close, then there’s a possibility that the experiment was conducted improperly or more trials need to be completed.
I hope this helps to give you a sense of how to set up an experiment in order to compare theoretical versus experimental probabilities.
- Home
- Probability
- Theoretical/Experimental Probability
>
>

Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.