dB: O que é um decibel?

Pressão sonora, nível sonoro e dB. O som é normalmente medido com microfones e eles respondem proporcionalmente à pressão sonora, p. Agora a potência em uma onda sonora, tudo mais igual, vai como o quadrado da pressão. (Da mesma forma, a energia elétrica em uma resistência vai como o quadrado da voltagem). O log de x2 é apenas 2 log x, portanto isto introduz um fator de 2 quando convertemos as relações de pressão em decibéis. A diferença no nível de pressão sonora entre dois sons com p1 e p2 é, portanto:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (ao longo de todo, o log é para a base 10).

O que acontece quando se reduz a potência sonora para metade? O log de 2 é 0.3010, então o log de 1/2 é -0.3, para uma boa aproximação. Então, se você reduzir a potência pela metade, você reduz a potência e o nível sonoro em 3 dB. Reduza-o novamente para metade (até 1/4 da potência original) e reduza o nível em mais 3 dB. Se você continuar reduzindo a potência pela metade, você tem estes rácios.

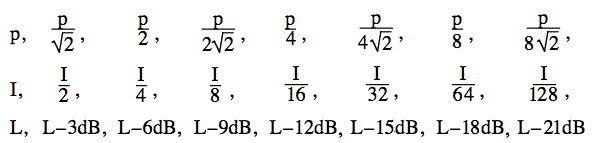
O que acontece se eu adicionar dois sons idênticos? Eu dobro a intensidade (aumento de 3 dB)? Ou eu dobro a pressão (aumento de 6 dB)? Esta pergunta frequentemente feita é um pouco sutil, por isso é discutida aqui no nosso FAQ.

Arquivos de som para mostrar o tamanho de um decibel

Vimos acima que a redução da potência pela metade reduz a pressão sonora em √2 e o nível sonoro em 3 dB. Isso é o que fizemos no primeiro arquivo gráfico e de som abaixo.

A primeira amostra de som é o ruído branco (uma mistura de uma vasta gama de frequências audíveis, análoga à luz branca, que é uma mistura de todas as frequências visíveis). A segunda amostra é o mesmo ruído, com a tensão reduzida por um factor de √2. Agora 1/√2 é aproximadamente 0,7, portanto -3 dB corresponde a reduzir a tensão ou a pressão a 70% do seu valor original. A linha verde mostra a tensão em função do tempo. A linha vermelha mostra uma decadência exponencial contínua com o tempo. Note que a tensão cai em 50% a cada segundo de amostra. Note, também, que uma duplicação da potência não faz uma grande diferença para o ruído. Discutiremos isto mais abaixo, mas é uma coisa útil a lembrar ao escolher equipamento de reprodução de som. Arquivos de som e animação de John Tann e George Hatsidimitris.

Qual é o tamanho de um decibel? Na próxima série, as amostras sucessivas são reduzidas em apenas um decibel.

Um decibel é da mesma ordem que o JND (Just Noticeable Difference) para o nível sonoro. Ao ouvir estes ficheiros, irá notar que o último é mais silencioso do que o primeiro, mas é bastante menos claro para o ouvido que o segundo de qualquer par é mais silencioso do que o seu predecessor. 10*log10(1.26) = 1, portanto para aumentar o nível de som em 1 dB, a potência deve ser aumentada em 26%, ou a voltagem em 12%.

E se a diferença for inferior a um decibel? Os níveis de som raramente são dados com casas decimais. A razão é que níveis sonoros que diferem menos de 1 dB são difíceis de distinguir, como mostra o exemplo seguinte.(Isto faz dos dB uma unidade de tamanho conveniente.)

0.3 dB passos. Você pode notar que o último é mais silencioso que o primeiro, mas é difícil notar a diferença entre os pares sucessivos. 10*log10(1,07) = 0,3, portanto para aumentar o nível sonoro em 0,3 dB, a potência deve ser aumentada em 7%, ou a tensão em 3,5%.

Níveis de referência standard (‘absolute’ sound level)

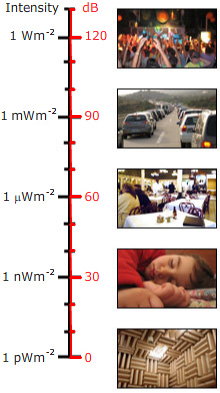Dissemos acima que o decibel é uma razão. Portanto, quando ele é usado para dar o nível sonoro para um único som em vez de uma relação, um nível de referência deve ser escolhido. Para o nível de pressão sonora, o nível de referência (para ar) é normalmente escolhido como pref = 20 micropascals (20 μPa), ou 0.02 mPa. Isto é muito baixo: são 2 décimos de bilionésimos de uma atmosfera. No entanto, trata-se do limite de sensibilidade do ouvido humano, na sua faixa sensível de frequência. (Normalmente esta sensibilidade só é encontrada em pessoas bastante jovens ou em pessoas que não foram expostas a música alta ou outros ruídos altos. Os sistemas musicais pessoais com altifalantes intra-auriculares são capazes de níveis sonoros muito elevados no ouvido, e acredita-se que alguns são responsáveis por grande parte da perda auditiva em adultos jovens em alguns países).

Então se você ler um nível de pressão sonora de 86 dB, significa que

20 log (p2/pref) = 86 dB

onde prefira é a pressão sonora do nível de referência, e p2 a do som em questão. Dividir ambos os lados por 20:

log (p2/pref) = 4,3

p2/pref = 104,3

4 é o log de 10 mil, 0,3 é o log de 2, portanto este som tem uma pressão sonora 20 mil vezes maior que a do nível de referência (p2/pref = 20.000) ou uma intensidade 400 milhões de vezes a intensidade de referência. 86 dB é um som alto mas não perigoso – desde que a exposição seja breve.

O que significa 0 dB? Este nível ocorre quando a intensidade medida é igual ao nível de referência, ou seja, é o nível sonoro correspondente a 0,02 mPa. Neste caso temos

nível sonoro = 20 log (pmeasured/pref) = 20 log 1 = 0 dB

Lembre-se que os decibéis medem uma relação. 0 dB ocorre quando se toma o log de uma razão de 1 (log 1 = 0). Então 0 dB não significa sem som, mas sim um nível sonoro onde a pressão sonora é igual à do nível de referência. Esta é uma pressão pequena, mas não zero. Também é possível ter níveis sonoros negativos: – 20 dB significaria um som com pressão 10 vezes menor que a pressão de referência, ou seja, 2 μPa.

Nem todas as pressões sonoras são igualmente altas. Isto porque o ouvido humano não responde igualmente a todas as frequências: somos muito mais sensíveis a sons na gama de frequências entre 1 kHz e 7 kHz (1000 a 7000 vibrações por segundo) do que a sons de frequência muito baixa ou alta. Por esta razão, os sonómetros são normalmente equipados com um filtro cuja resposta à frequência é um pouco parecida com a do ouvido humano. (Mais sobre estes filtros abaixo.) Se for utilizado o “filtro de ponderação”, o nível de pressão sonora é dado em unidades de dB(A) ou dBA. O nível de pressão sonora na escala dBA é fácil de medir e por isso é amplamente utilizado. Uma razão pela qual é diferente do ruído é porque o filtro não responde da mesma forma que o ouvido. Para entender a sonoridade de um som, a primeira coisa que você precisa fazer é consultar algumas curvas que representam a resposta de freqüência do ouvido humano, dadas abaixo. (Alternativamente, você pode medir sua própria resposta auditiva.) Outra razão é que a audição humana não é logarítmica.

Medidas logarítmicas

Por que usamos decibéis? O ouvido é capaz de ouvir uma gama muito grande de sons: a proporção da pressão sonora que causa danos permanentes devido à curta exposição ao limite que os ouvidos (não danificados) podem ouvir é superior a um milhão. Para lidar com tal alcance, as unidades logarítmicas são úteis: o log de um milhão é 6, pelo que esta relação representa uma diferença de 120 dB. A audição não é intrinsecamente logarítmica em resposta. (As medidas logarítmicas também são úteis quando um som (brevemente) aumenta ou diminui exponencialmente ao longo do tempo. Isto acontece em muitas aplicações envolvendo ganho ou perda proporcional.)

Os filtros usados para dBA e dB(C)

O filtro de nível sonoro mais usado é a escala A, que corresponde mais ou menos ao inverso da curva de igual intensidade de 40 dB (a 1 kHz). Usando este filtro, o sonómetro é assim menos sensível a frequências muito altas e muito baixas. As medições feitas nesta escala são expressas em dBA. A escala C varia pouco em várias oitavas e é assim adequada para medições subjectivas apenas para níveis sonoros moderados a altos. As medições feitas nesta escala são expressas como dB(C). Existe também uma escala de ponderação B (raramente utilizada), intermediária entre A e C. A figura abaixo mostra a resposta do filtro A (esquerda) e do filtro C, com ganhos em dB dados em relação a 1 kHz. (Para uma introdução aos filtros, ver filtros RC, integradores e diferenciadores).



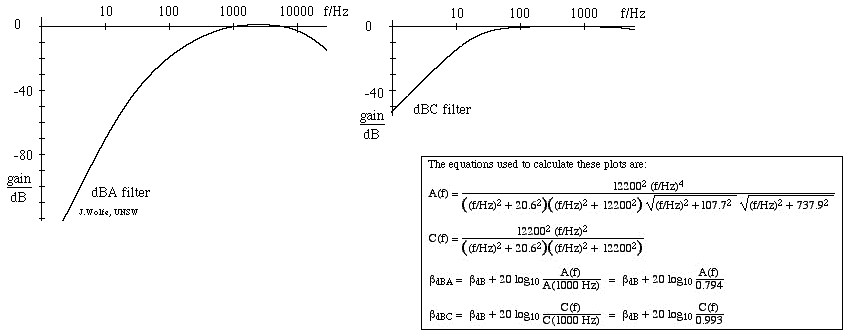
Nos sites de acústica da música e acústica da fala, plotamos os espectros sonoros em dB. A razão para esta prática comum é que a gama de pressões sonoras medidas é grande.

dB(G) as medidas usam um filtro de banda estreita que dá alta ponderação a frequências entre 1 e 20 Hz, e baixa ponderação a outros. Assim, ele dá grandes valores para sons e infra-sons que não podem ser ouvidos prontamente. ISO 7196:1995

Loudness, fones e ossos, curvas de resposta auditiva

O fone é uma unidade que está relacionada a dB pela resposta de frequência psicofisicamente medida do ouvido. A 1 kHz, as leituras em phons e dB são, por definição, as mesmas. Para todas as outras frequências, a escala fonética é determinada pelos resultados de experimentos nos quais voluntários foram solicitados a ajustar a audibilidade de um sinal a uma determinada frequência até que julgassem sua audibilidade igual a de um sinal de 1 kHz. Para converter de dB para fonos, é necessário um gráfico de tais resultados. Tal gráfico depende do nível sonoro: torna-se mais plano em níveis sonoros elevados.

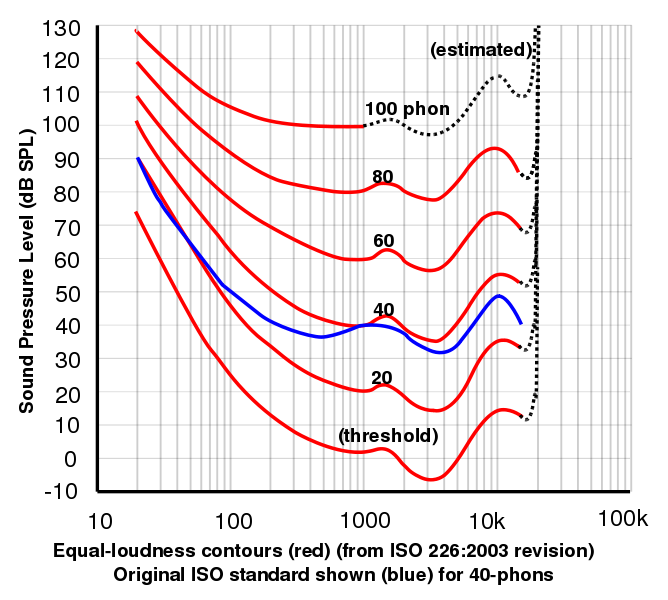
Este gráfico, cortesia de Lindosland, mostra os dados de 2003 da International Standards Organisation para curvas de igual audibilidade determinadas experimentalmente. Os gráficos de igual altura em função da frequência são geralmente chamados genericamente de curvas Fletcher-Munson após o trabalho original de Fletcher, H. e Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Você pode fazer as suas próprias curvas usando o nosso site de resposta auditiva.

O som é derivado de medidas psicofísicas que envolveram voluntários ajustando sons até que eles os julgassem duas vezes mais altos. Isto permite relacionar a sonoridade percebida com os fonemas. Um sone é definido para ser igual a 40 phons. Experimentalmente, verificou-se que, acima de 40 fones, um aumento de 10 dB no nível de som corresponde aproximadamente a uma duplicação percebida da sonoridade. Assim, a aproximação é utilizada na definição do sone: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon, etc.



Esta relação implica que a sonoridade e a intensidade estão relacionadas por uma lei de potência: a sonoridade nos sones é proporcional ao (intensidade)log 2 = (intensidade)0.3.

Não seria ótimo ser capaz de converter de dB (que pode ser medido por um instrumento) para sones (que aproxima a sonoridade como percebida pelas pessoas)? Isto às vezes é feito usando tabelas que você pode encontrar nos manuais de acústica. No entanto, se não se importar com uma aproximação bastante grosseira, pode dizer que a curva de ponderação A aproxima-se da resposta da frequência humana a níveis sonoros baixos a moderados, pelo que dB(A) é muito mais ou menos o mesmo que os fonos, numa gama limitada de níveis baixos. Então pode-se usar a relação logarítmica entre os sones e os fones descrita acima.

Nível de gravação e decibéis

Medidores que medem o nível de gravação ou de saída em equipamento electrónico de áudio (consolas de mistura, etc) estão quase sempre a gravar a tensão AC rms (ver links para saber mais sobre AC e rms). Para uma dada resistência R, a potência P é V2/R, portanto
diferença no nível de tensão = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, ou

nível de tensão absoluto = 20 log (V/Vref)

onde Vref é uma tensão de referência. Então qual é a voltagem de referência?

O nível óbvio a escolher é um volt rms, e neste caso o nível é escrito como dBV. Isto é racional, e também conveniente com placas analógico-digitais cujo intervalo máximo é frequentemente de cerca de um volts rms. Então é preciso lembrar de manter o nível em dBV negativo (menos de um volts) para evitar cortar os picos do sinal, mas não muito negativo (assim seu sinal ainda é muito maior do que o ruído de fundo).

Algumas vezes você verá dBm. Isto costumava significar decibéis de energia elétrica, com respeito a um milliwatt, e às vezes ainda significa. No entanto, é complicado por razões históricas. Em meados do século XX, muitas linhas de áudio tinham uma impedância nominal de 600 Ω. Se a impedância é puramente resistiva, e se você definir V2/600 Ω = 1 mW, então você obtém V = 0,775 volts. Então, desde que você estivesse usando uma carga 600 Ω, 1 mW de potência era 0 dBm, que era 0,775 V, então você calibrou seus medidores de nível assim. O problema surgiu porque, uma vez que um medidor de nível que mede tensão é calibrado assim, ele vai ler 0 dBm a 0,775 V mesmo que não esteja conectado a 600 Ω Então, talvez ilogicamente, dBm às vezes significará dB em relação a 0,775 V. (Quando eu era um menino, as calculadoras eram caras, então eu usei a velha régua de cálculo do pai, que tinha o fator 0,775 marcado na janela do cursor para facilitar tais cálculos).

Como converter dBV ou dBm em dB de nível sonoro? Não há uma maneira simples. Depende de como você converte a energia elétrica em potência sonora. Mesmo que o seu sinal elétrico esteja conectado diretamente a um alto-falante, a conversão dependerá da eficiência e impedância do seu alto-falante. E, claro, pode haver um amplificador de potência e várias complicações acústicas entre onde você mede os dBV na mesa de mixagem e onde os seus ouvidos estão no campo sonoro.

Intensidade, radiação e dB

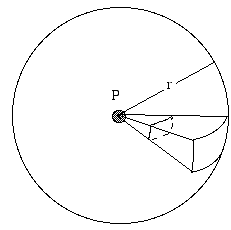
How does sound level (or radio signal level, etc.) depends on distance from the source?

Uma fonte que emite radiação igualmente em todas as direcções é chamada isotrópica. Considere uma fonte isolada de som, longe de qualquer superfície reflectora – talvez uma ave cantando alto no ar. Imagine uma esfera com raio r, centrada na fonte. A fonte produz uma potência total P, continuamente. Esta potência sonora espalha-se e passa através da superfície da esfera. Se a fonte é isotrópica, a intensidade I é a mesma em todo o lado nesta superfície, por definição. A intensidade I é definida como a potência por unidade de área. A área da superfície da esfera é 4πr2, portanto a potência (no nosso exemplo, a potência sonora) passando por cada metro quadrado de superfície é, por definição:

I = P/4πr2.

Então, vemos que, para uma fonte isotrópica, a intensidade é inversamente proporcional ao quadrado da distância da fonte:

I2/I1 = r12/r22.

Mas a intensidade é proporcional ao quadrado da pressão sonora, para que pudéssemos escrever igualmente:

p2/p1 = r1/r2.

Então, se dobrarmos a distância, reduzimos a pressão sonora por um fator de 2 e a intensidade por um fator de 4: em outras palavras, reduzimos o nível sonoro em 6 dB. Se aumentarmos r por um factor de 10, diminuímos o nível em 20 dB, etc.

Ser avisado, no entanto, que muitas fontes não são isotrópicas, especialmente se o comprimento de onda for menor que, ou de um tamanho comparável com a fonte. Além disso, os reflexos são muitas vezes bastante importantes, especialmente se o solo estiver próximo, ou se você estiver dentro de casa.

Pressão, intensidade e impedância específica

Para ondas acústicas, a impedância acústica específica z é definida como a razão entre a pressão acústica p e a velocidade média das partículas u, devido ao som ave, z = p/u . Na impedância acústica, intensidade e potência, mostramos como relacionar a pressão acústica RMS p com a intensidade I:
I = p2/z

Para o ar, a impedância acústica específica z é 420 kg.s-1.m-2 = 420 Pa.s.m-1. Para água (doce), a impedância acústica específica para água é de 1,48 MPa.s.m-1. Portanto, uma onda sonora na água com a mesma pressão tem uma intensidade muito menor do que uma no ar.

dBi e radiação que varia com a direção

A radiação que varia com a direção é chamada anisotrópica. Para muitos casos em comunicação, a radiação isotrópica é um desperdício: por que emitir uma fração substancial de energia para cima se o receptor está, como você, relativamente perto do nível do solo. Para um som de comprimento de onda curto (incluindo a maioria do alcance importante para a fala), um megafone pode ajudar a tornar a sua voz mais anisotrópica. Para o rádio, uma vasta gama de designs permite que as antenas sejam altamente anisotrópicas tanto para a transmissão como para a recepção. ssim, quando estiver interessado em emitir (ou receber de) uma determinada direcção, pretende que a relação de intensidade medida nessa direcção, a uma determinada distância, seja superior à medida à mesma distância de um radiador isotrópico (ou recebido por um receptor isotrópico). Essa relação é chamada de ganho; expresse a relação em dB e você tem o ganho em dBi para esse radiador. Esta unidade é usada principalmente para antenas, tanto para transmitir como para receber, mas às vezes é usada para fontes sonoras e microfones direcionais.

Problemas de amostra

Poucas pessoas escreveram pedindo exemplos de utilização de dB nos cálculos. Então…
• Tudo o resto é igual, quanto mais alto é conduzido (no seu alcance linear) por um amplificador de 100 W do que por um amplificador de 10 W?

  As potências diferem por um fator de dez, que, como vimos acima, é de 10 dB. Tudo o resto aqui significa que as respostas de frequência são iguais e que é utilizado o mesmo sinal de entrada, etc. Portanto, a dependência da frequência deve ser a mesma. 10 dB corresponde a 10 fons. Para que se perceba uma duplicação da sonoridade, é necessário um aumento de 10 fones. Assim, o alto-falante acionado pelo amplificador de 100 W é duas vezes mais alto do que quando acionado pelos 10 W, assumindo que você permaneça na faixa linear e não distorça ou destrua o alto-falante. (O amplificador de 100 W produz o dobro dos sons que o amplificador de 10 W.)

• I está a uma distância R de uma pequena fonte de som (tamanho muito menor que R), ao nível do chão, ao ar livre, onde os reflexos podem ser negligenciados. O nível de som é L. Se eu agora me mover para uma distância nR (n um número, e nR ainda muito maior do que o tamanho da fonte), qual será o novo nível de som?

  Primeiro, note que o descuido dos reflexos é muito importante. Este cálculo não vai funcionar dentro de uma sala, onde os reflexos da parede (produzindo colectivamente reverberação) tornam o cálculo bastante difícil. Ao ar livre, a intensidade sonora é proporcional a 1/r2, onde r é a distância da fonte. (A constante de proporcionalidade depende de quão bem o solo reflete, e não nos preocupa aqui, pois irá aproximadamente cancelar no cálculo, desde que r seja razoavelmente grande). Assim, se aumentarmos r de R para nR, diminuiremos a intensidade de I para I/n 2.

  A diferença de decibéis entre os dois sinais de intensidade I 2 e I 1 é definida acima para ser

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  Por exemplo, se n é 2 (isto é, se nos afastarmos o dobro), a intensidade é reduzida por um factor de quatro e o nível sonoro cai de L para (L – 6dB).

• Se, em condições ideais de silêncio, um jovem consegue ouvir um som de 1 kHz a 0 dB emitido por um altifalante (talvez um softspeaker?), até que ponto a potência do altifalante deve ser aumentada para elevar o som para 110 dB (um nível perigosamente alto mas sobrevivível)?

  A diferença em decibéis entre os dois sinais de potência P2 e P1 é definida acima para ser

  ΔL = 10 log (P2/P1) dB, elevando assim 10 para a potência destas duas quantidades iguais:
  10L/10 = P2/P1 so:
  P2/P1 = 10110/10 = 1011 = cem mil milhões.

  que é uma demonstração de que o ouvido humano tem uma faixa dinâmica notavelmente grande, talvez maior que a do olho.

• Um amplificador tem uma entrada de 10 mV e uma saída de 2 V. Qual é o seu ganho de voltagem em dB?

  Tensão, como a pressão, aparece ao quadrado em expressões de potência ou intensidade. (A potência dissipada em um resistor R é V2/R.) Então, por convenção, nós definimos:

  ganho = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (Nos casos acústicos acima, vimos que a razão de pressão, expressa em dB, era a mesma que a razão de potência: essa foi a razão para o fator 20 na definição de dB para pressão. Vale notar que, no exemplo do ganho de tensão, é pouco provável que o ganho de potência do amperímetro seja igual ao ganho de tensão, que é definido pela convenção aqui utilizada. A potência é proporcional ao quadrado da voltagem em uma determinada resistência. Contudo, as impedâncias de entrada e saída dos amplificadores são muitas vezes bastante diferentes. Por exemplo, um amplificador tampão ou seguidor de emissor tem um ganho de voltagem de cerca de 1, mas um grande ganho de corrente).

• Qual é a diferença, em dB, entre a irradiação (intensidade da luz) na terra (8,3 minutos de luz do sol) e em Urano (160 minutos de luz)?

  Como o som, a intensidade da luz isotrópica diminui à medida que r-2, portanto a relação de intensidade é (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Saúde e segurança ocupacional

Diferentes países e províncias têm obviamente diferentes leis relativas à exposição ao ruído no trabalho, que são aplicadas com diferentes entusiasmos. Muitas dessas regulamentações têm um limite de exposição ao ruído contínuo de 85 dB(A), para um turno de 8 horas. Para cada 3 dB de aumento, a exposição permitida é reduzida pela metade. Portanto, se você trabalha em uma boate onde a música amplificada produz 100 dB(A) perto dos seus ouvidos, a exposição permitida é de 15 minutos. Há um limite para ruídos de impulso como armas de fogo ou ferramentas que usam tiros explosivos. (por exemplo, o pico de 140 dB não deve ser excedido em nenhum momento do dia.) Existem muitos documentos que fornecem conselhos sobre como reduzir a exposição ao ruído na fonte (ou seja, baixar o nível da música), entre a fonte e o ouvido (ou seja, afastar-se dos altifalantes num concerto) e no ouvido (ou seja, usar tampões auriculares ou protectores auriculares industriais). O gerenciamento do ruído e a proteção da audição no trabalho é o código de prática no estado de New South Wales, Austrália (endereço do autor).

algumas FAQs

• Quão barulhento é um avião? Um trem? Uma pessoa a cantar? Um cão a ladrar? Uma ferramenta eléctrica? As respostas a esta pergunta variam consideravelmente. Depende muito de quão longe você está, se você está dentro de casa ou não, se há reverberação, quão forte é a fonte em particular e qual é o seu espectro. Dar valores, sem ser muito específico sobre as condições, seria um tanto enganador. Porque o resto desta página pretende ser confiável, até onde vai, eu prefiro não dar valores aqui.
• Como é que se “adiciona decibéis”?, significando Que nível de som se obtém quando se adiciona nível a ao nível b? Se as fontes são coerentes (o que geralmente significa que elas vêm da mesma fonte), então pode haver efeitos de interferência complicados. Na maioria dos casos, onde as fontes são independentes, pode-se adicionar as intensidades e depois converter para decibéis. No entanto, se lhe forem dados os níveis de som em dB(A), não é tão fácil voltar à intensidade, e é preciso saber algo sobre o espectro do som. Se você conhece a distribuição do som em diferentes bandas de frequência, você pode usar o applet neste link.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.