Distribuição Marginal

p> Distribuições de Probabilidade > Distribuição Marginal

O que é uma distribuição Marginal?

Veja o vídeo ou leia o artigo abaixo:
div>Por favor aceite estatísticas, cookies de marketing para ver este vídeo.

A definição técnica pode ser um pouco insensível para olhar:

Definição de uma distribuição marginal = Se X e Y são variáveis aleatórias discretas e f (x,y) é o valor de
a sua distribuição de probabilidade conjunta em (x,y), as funções dadas por:
g(x) = Σy f (x,y) e h(y) = Σx f (x,y) são as distribuições marginais de X e Y , respectivamente.

Se você é ótimo com equações, isso é provavelmente tudo que você precisa saber. Ele diz-lhe como encontrar uma distribuição marginal. Mas se essa fórmula lhe dá dor de cabeça (o que faz com a maioria das pessoas!), você pode usar uma tabela de distribuição de freqüência para encontrar uma distribuição marginal.

Uma distribuição marginal recebe o seu nome porque aparece nas margens de uma tabela de distribuição de probabilidade.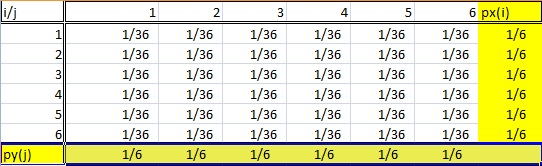

Obviamente, não é tão simples quanto isso. Você não pode simplesmente olhar para qualquer tabela de distribuição de freqüência antiga e dizer que a última coluna (ou linha) é uma “distribuição marginal”. As distribuições marginais seguem algumas regras:

• A distribuição deve ser a partir de dados bivariados. Bivariada é apenas outra forma de dizer “duas variáveis”, como X e Y. Na tabela acima, as variáveis aleatórias i e j vêm do lançamento de dois dados.
• Uma distribuição marginal é onde você está interessado apenas em uma das variáveis aleatórias . Em outras palavras, ou X ou Y. Se você olhar para a tabela de probabilidade acima, as probabilidades de soma de uma variável são listadas na linha inferior e as outras probabilidades de soma são listadas na coluna da direita. Portanto, esta tabela tem duas distribuições marginais.

Diferença entre Distribuição Marginal e Distribuição Condicional.

Uma distribuição condicional é onde estamos interessados apenas em uma determinada subpopulação de todo o nosso conjunto de dados. No exemplo de rolamento de dados, isto poderia ser “rolando um dois” ou “rolando um seis”. A imagem abaixo mostra duas subpopulações destacadas (e portanto, duas distribuições condicionais).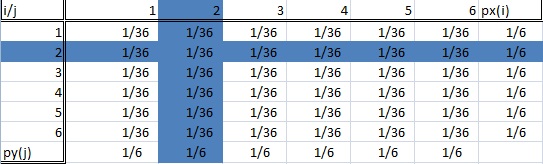

Como calcular a probabilidade de distribuição marginal

p>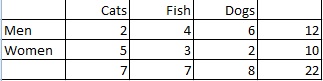

P>Pergunta de exemplo: Calcular a distribuição marginal de preferência de animais de estimação entre homens e mulheres:
Solução:
Passo 1: Conte o número total de pessoas. Neste caso o total é dado na coluna da direita (22 pessoas).
Passo 2: Conte o número de pessoas que preferem cada tipo de animal e depois transforme a proporção em probabilidade:
Pessoas que preferem gatos: 7/22 = .32
Pessoas que preferem peixes: 7/22 = .32
Pessoas que preferem cães: 8/22 = .36
Tip: Você pode verificar sua resposta certificando-se de que todas as probabilidades somam até 1.

Pergunta de amostra 2 (Eventos mutuamente exclusivos): Se P(A) = 0.20, P(b) = 0.70, e ambos os eventos são mutuamente exclusivos, encontre P(B’∩A), P(B’∩A’) e P(B∩A’).
Se não estiver familiarizado com esta notação, P(A’) significa “não A”, ou o complemento. P(B’∩A) significa “a intersecção de não B e A”).

Resposta:
Você poderia descobrir as probabilidades individualmente, mas elas são muito mais fáceis de descobrir usando uma tabela.

Passo 1: Preencha uma tabela de frequência com a informação dada. A probabilidade total deve ser igual a 1, então você pode adicionar isso às margens (totais) também. A simples adição/algebra preenche os espaços em branco nas margens. Por exemplo, na linha inferior 0.70 + x = 1.00 então O total marginal para B’ deve ser 0.30.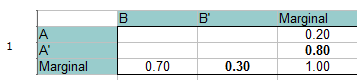
br>Passo 2: Adicione 0 para a intersecção de A e B, na parte superior esquerda da tabela. Você pode fazer isso porque A e B são mutuamente exclusivos e não podem acontecer juntos.
br>passo 3: Preencha o resto dos espaços em branco usando adição/álgebra simples.
br>

Leitura da tabela (veja as interseções das duas probabilidades indicadas):
P(B’∩A) = 0.20
P(B’∩A’) = 0.10
P(B∩A’) = 0.70.

P>Pergunta de amostra 3 (Eventos independentes): Se P(A) = 0.20, P(b) = 0.70, e ambos os eventos são independentes, encontre P(B’∩A), P(B’∩A’) e P(B∩A’).

Resposta: Desta vez, A e B são independentes, portanto a probabilidade de ambos acontecerem ao mesmo tempo é de 0.14 (P(A)*P(B) = 0.20 * 0.70 = 0.14). Este valor vai para a parte superior esquerda (intersecção de A e B). Preencha o resto da tabela exatamente da mesma forma que nos passos acima.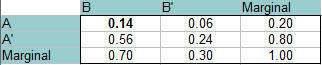
br>Leia as respostas da tabela (das interseções das duas probabilidades):
P(B’∩A): 0.06
P(B’∩A’): 0.24
P(B∩A’): 0.56.

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 e 571, 2002.
Agresti A. (1990) Categorical Data Analysis (Análise de Dados Categóricos). John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Segunda Edição (Schaum’s Easy Outlines) 2ª Edição. McGraw-Hill Education

——————————————————————————
p>Need help with a homework or test question? Com o Chegg Study, você pode obter soluções passo-a-passo para suas perguntas de um especialista na área. Os seus primeiros 30 minutos com um tutor do Chegg são grátis!