Qual é o truque do kernel? Porque é importante?
Ao falar sobre kernels na aprendizagem de máquinas, muito provavelmente a primeira coisa que vem à sua mente é o modelo de máquinas vetoriais de suporte (SVM) porque o truque do kernel é amplamente usado no modelo SVM para fazer a ponte entre linearidade e não-linearidade.
Para ajudá-lo a entender o que é um kernel e porque é importante, eu vou introduzir o básico do modelo SVM primeiro.
O modelo SVM é um modelo supervisionado de aprendizagem de máquina que é usado principalmente para classificações (mas também pode ser usado para regressão!). Ele aprende como separar diferentes grupos, formando limites de decisão.

/div>
No gráfico acima, notamos que existem duas classes de observações: os pontos azuis e os pontos roxos. Há toneladas de maneiras de separar essas duas classes, como mostrado no gráfico à esquerda. Entretanto, queremos encontrar o “melhor” hiperplano que poderia maximizar a margem entre estas duas classes, o que significa que a distância entre o hiperplano e os pontos de dados mais próximos de cada lado é a maior. Dependendo de qual lado do hiperplano um novo ponto de dados localiza, poderíamos atribuir uma classe à nova observação.
Soa simples no exemplo acima. No entanto, nem todos os dados são separáveis linearmente. Na verdade, no mundo real, quase todos os dados são distribuídos aleatoriamente, o que torna difícil separar as diferentes classes linearmente.

Por que é importante usar o truque do kernel?
Como pode ver na figura acima, se encontrarmos uma forma de mapear os dados do espaço bidimensional para o espaço tridimensional, poderemos encontrar uma superfície de decisão que se divide claramente entre diferentes classes. Meu primeiro pensamento sobre este processo de transformação de dados é mapear todos os dados apontam para uma dimensão superior (neste caso, 3 dimensões), encontrar o limite, e fazer a classificação.
Isso soa bem. Entretanto, quando há cada vez mais dimensões, os cálculos dentro desse espaço se tornam mais e mais caros. Isto é quando entra o truque do kernel. Ele nos permite operar no espaço da característica original sem calcular as coordenadas dos dados em um espaço dimensional superior.
Vejamos um exemplo:
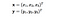
Aqui x e y são dois pontos de dados em 3 dimensões. Vamos supor que precisamos mapear x e y para o espaço de 9 dimensões. Precisamos de fazer os seguintes cálculos para obter o resultado final, que é apenas um escalar. A complexidade computacional, neste caso, é O(n²).

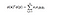
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
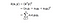
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Quaisquer cálculos envolvendo os produtos ponto (x, y) podem utilizar o truque do kernel.
Diferentes funções do kernel
Existem kernels diferentes. Os mais populares são o kernel polinomial e o kernel da função de base radial (RBF).
“Intuitivamente, o kernel polinomial olha não só para as características dadas das amostras de entrada para determinar a sua semelhança, mas também para as combinações destas” (Wikipedia), tal como o exemplo acima. Com n características originais e d graus de polinomial, o kernel polinomial produz n^d características expandidas.
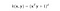
O kernel RBF também é chamado de kernel Gaussiano. Há um número infinito de dimensões no espaço de características porque pode ser expandido pela Série Taylor. No formato abaixo, o parâmetro γ define quanta influência tem um único exemplo de treinamento. Quanto maior for, mais próximos outros exemplos devem ser afetados (documentação do sklearn).
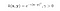
Existem diferentes opções para as funções do kernel na biblioteca do sklearn em Python. Você pode até mesmo construir um kernel personalizado se necessário.
The End
O truque do kernel soa como um plano “perfeito”. Entretanto, uma coisa crítica a ter em mente é que quando mapeamos dados para uma dimensão superior, há chances de que possamos ajustar em demasia o modelo. Assim, escolher a função correta do kernel (incluindo os parâmetros certos) e regularização são de grande importância.
Se você está curioso sobre o que é regularização, eu escrevi um artigo falando sobre o meu entendimento dela e você pode encontrá-la aqui.
Espero que você goste deste artigo. Como sempre, por favor me avise se você tiver alguma pergunta, comentário, sugestão, etc. Obrigado por ler 🙂