Solving the Königsberg Bridge Problem
This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)
The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem
Have a look at the map above.
It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.
A map of the city is below. Você pode olhar para qualquer um dos diagramas – ambos capturam os pedaços de informação chave: quais blocos de terra estão conectados a quais outros blocos de terra, e por quantas pontes.
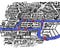
Em linguagem técnica, estamos representando isso como um gráfico. Os blobs de terra são os vértices, e as pontes são as bordas. Mas isso não é importante.
O problema é se é possível encontrar uma rota que passa por cada ponte exatamente uma vez. Isso significa que, na nossa caminhada pela cidade, queremos que a nossa rota atravesse cada ponte, mas ela não pode atravessá-la duas ou três vezes… Basicamente, se você se encontrar na mesma ponte que estava anteriormente, o caminho é inválido. Se você terminar sua caminhada e houver uma ponte que você não atravessou, então sua rota é inválida.
The Solution
Considerar cada borrão de terra. Cada ponte está ligada a dois blobs de terra (é assim que as pontes funcionam). Cada blob de terra tem um número ímpar de pontes ligadas.
Agora, vamos considerar como seria uma caminhada válida.
Como você vai na sua caminhada, você grava em um bloco de notas cada vez que você está em um determinado blob de terra. Por exemplo, se você começar no extremo mais sul da cidade, você faz uma anotação disso (tire uma foto, compre uma lembrança…) e se você se encontrar lá novamente, você aumenta a contagem para o setor sul para dois.
Para cada bolha de terra há dois casos
(1) esta é uma secção da cidade em que não começamos a nossa caminhada, nem terminamos a nossa caminhada lá
(2) esta é uma secção da cidade ou começamos a nossa caminhada, ou terminamos a nossa caminhada, ou ambas.
Claramente, há no máximo 2 secções da cidade do segundo tipo. Não podemos começar em dois lugares ao mesmo tempo, nem podemos terminar em dois lugares ao mesmo tempo.
Como há quatro seções da cidade, isso significa que há pelo menos duas seções da cidade, em nossa caminhada, que não terminamos nem começamos. Vamos escolher uma delas.
Quando entramos nesse setor, usamos uma ponte, e sempre que a deixamos, usamos outra. Mas, cada setor tem um número ímpar de pontes presas a ele! Isso é uma contradição. Para ver porquê, lembrem-se que cada sector ou tem 3 pontes, ou tem 5 pontes presas.
Se estivermos no sector uma vez, só podemos usar duas das suas pontes. Se estivermos nele duas vezes, usaríamos até quatro das suas pontes (ou ficaríamos sem pontes, se ele tivesse apenas três pontes). Se estivéssemos nele três vezes, precisaríamos de 6 pontes, o que não podemos ter. Assim, a exigência de entrarmos e sairmos de um sector da cidade que não é o nosso ponto de partida ou de chegada contradiz o facto de que o número de pontes de ligação é estranho para cada sector.