Tipos de Interpolação – Vantagens e Desvantagens
Métodos de Interpolação
Interpolação é o processo de usar pontos com valores conhecidos ou pontos de amostra para estimar valores em outros pontos desconhecidos. Pode ser usado para prever valores desconhecidos para quaisquer dados de pontos geográficos, tais como elevação, precipitação, concentrações químicas, níveis de ruído, e assim por diante.
Os métodos de interpolação disponíveis estão listados abaixo.
Ponderação da Distância Inversa (IDW)
O interpolador de Ponderação da Distância Inversa assume que cada ponto de entrada tem uma influência local que diminui com a distância. Ele pesa os pontos mais próximos da célula de processamento maiores do que aqueles mais distantes. Um número especificado de pontos, ou todos os pontos dentro de um raio especificado pode ser usado para determinar o valor de saída de cada local. O uso deste método assume que a variável sendo mapeada diminui em influência com a distância da sua localização amostrada.
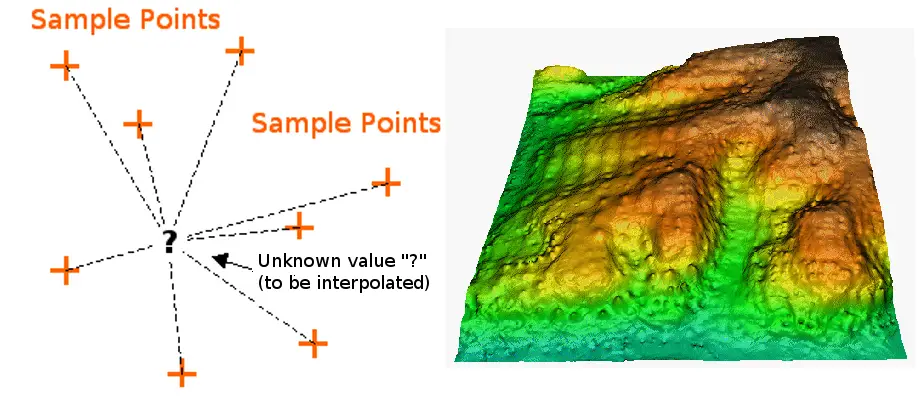
IDW Interpolação; Cortesia: QGIS
O algoritmo de Ponderação por Distância Inversa (IDW) é efectivamente um interpolador de média móvel que é normalmente aplicado a dados altamente variáveis. Para certos tipos de dados é possível retornar ao local de coleta e registrar um novo valor que é estatisticamente diferente da leitura original, mas dentro da tendência geral para a área.
A superfície interpolada, estimada usando uma técnica de média móvel, é inferior ao valor máximo local e maior que o valor mínimo local.
 p>IDW Superfície Interpolada; Cortesia:ESRI
p>IDW Superfície Interpolada; Cortesia:ESRI IDW interpolação implementa explicitamente a suposição de que as coisas que estão próximas umas das outras são mais parecidas do que aquelas que estão mais distantes. Para prever um valor para qualquer local não medido, o IDW utilizará os valores medidos em torno do local da previsão. Os valores medidos mais próximos do local de previsão terão mais influência sobre o valor previsto do que aqueles mais distantes. Assim, o IDW assume que cada ponto medido tem uma influência local que diminui com a distância. A função IDW deve ser usada quando o conjunto de pontos é suficientemente denso para capturar a extensão da variação da superfície local necessária para a análise. O IDW determina os valores das células usando um conjunto combinado de pontos de amostra ponderados linearmente. Ele pesa os pontos mais próximos do local de previsão maior que aqueles mais distantes, daí o nome distância inversa ponderada.
A técnica IDW calcula um valor para cada nó de grade examinando os pontos de dados ao redor que estão dentro de um raio de pesquisa definido pelo usuário. Alguns ou todos os pontos de dados podem ser usados no processo de interpolação. O valor do nó é calculado através da média da soma ponderada de todos os pontos. Pontos de dados que estão progressivamente mais distantes do nó influenciam o valor calculado muito menos do que aqueles que estão mais próximos do nó.
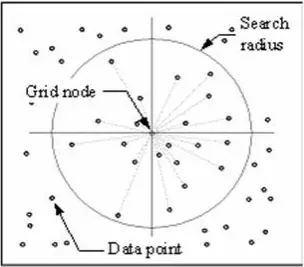
É gerado um raio ao redor de cada nó de grade a partir do qual os pontos de dados são selecionados para serem usados no cálculo. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. Outro método de média ponderada, a equação básica usada na interpolação de vizinho natural é idêntica à usada na interpolação IDW. Este método pode lidar eficientemente com grandes conjuntos de dados de pontos de entrada. Ao usar o método Natural Neighbor, coordenadas locais definem a quantidade de influência que qualquer ponto de dispersão terá nas células de saída.
O método Natural Neighbour é uma técnica de estimativa geométrica que usa regiões naturais de vizinhança geradas em torno de cada ponto no conjunto de dados.
Like IDW, este método de interpolação é um método de interpolação de média ponderada. Entretanto, ao invés de encontrar o valor de um ponto interpolado usando todos os pontos de entrada ponderados pela sua distância, a interpolação Vizinhos Naturais cria uma Triangulação de Delauney dos pontos de entrada e seleciona os nós mais próximos que formam um casco convexo ao redor do ponto de interpolação, depois pondera seus valores por área proporcional. Este método é mais apropriado onde os pontos de dados de amostra são distribuídos com densidade desigual. É uma boa técnica de interpolação de propósito geral e tem a vantagem de não ser necessário especificar parâmetros como raio, número de vizinhos ou pesos.

Natural IDW: Cortesia: ESRI
Esta técnica foi concebida para honrar os valores mínimos e máximos locais no ficheiro de pontos e pode ser definida para limitar os excessos de valores locais altos e os baixos valores locais baixos. O método permite assim a criação de modelos de superfície precisos a partir de conjuntos de dados que são muito escassamente distribuídos ou muito lineares na distribuição espacial.
Advantages
- Handles grande número de pontos de amostra eficientemente.
br>
Spline
Spline estima valores usando uma função matemática que minimiza a curvatura total da superfície, resultando em uma superfície lisa que passa exatamente pelos pontos de entrada.

Spline: Cortesia: ESRI
Conceptualmente, é análogo dobrar uma folha de borracha para passar por pontos conhecidos enquanto minimiza a curvatura total da superfície. Ela se ajusta a uma função matemática para um número especificado de pontos de entrada mais próximos enquanto passa através dos pontos de amostra. Este método é melhor para variar suavemente as superfícies, tais como elevação, altura dos lençóis freáticos ou concentrações de poluição.
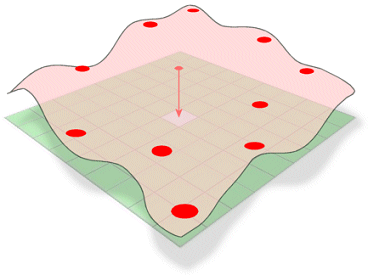
O método Spline de interpolação estima valores desconhecidos ao dobrar uma superfície através de valores conhecidos.
Existem dois métodos spline: regularizado e de tensão.
Um método regularizado cria uma superfície suave, que muda gradualmente com valores que podem estar fora do intervalo de dados da amostra. Ele incorpora a primeira derivada (inclinação), segunda derivada (taxa de mudança na inclinação) e terceira derivada (taxa de mudança na segunda derivada) em seus cálculos de minimização.
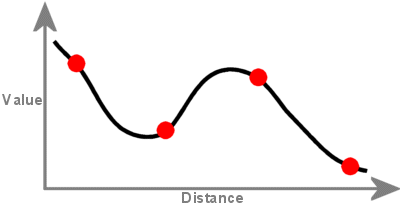
Uma superfície criada com interpolação Spline passa por cada ponto de amostra e pode exceder o intervalo de valores do conjunto de pontos de amostra.
Embora um spline de tensão utilize apenas a primeira e segunda derivadas, ele inclui mais pontos nos cálculos Spline, o que normalmente cria superfícies mais suaves mas aumenta o tempo de cálculo.
Este método puxa uma superfície sobre os pontos adquiridos resultando em um efeito esticado. Spline usa linhas curvas (método das linhas curvas) para calcular os valores das células.
Escolhendo um peso para Interpolações Spline
Spline regularizado: Quanto maior for o peso, mais suave será a superfície. Pesos entre 0 e 5 são adequados. Os valores típicos são 0, .001, .01, .1,e .5.
Estriado de tensão: Quanto mais alto o peso, mais grossa a superfície e mais os valores estão de acordo com o intervalo de dados da amostra. Os valores de peso devem ser maiores ou iguais a zero. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Kriging procedure that generates an estimated surface from a scattered set of points with z-values. Kriging assume que a distância ou direção entre pontos de amostra reflete uma correlação espacial que pode ser usada para explicar a variação na superfície. A ferramenta Kriging ajusta uma função matemática a um número especificado de pontos, ou a todos os pontos dentro de um raio especificado, para determinar o valor de saída para cada local. Kriging é um processo de múltiplas etapas; inclui análise estatística exploratória dos dados, modelagem de variograma, criação da superfície e (opcionalmente) exploração de uma superfície de variância. Kriging é mais apropriado quando você sabe que há uma distância espacialmente correlacionada ou um viés direcional nos dados. É frequentemente usado em ciência do solo e geologia.
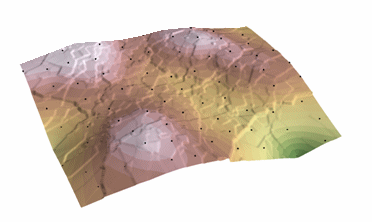
Kriging: Cortesia: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
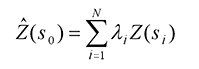
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Entretanto, com o método kriging, os pesos são baseados não apenas na distância entre os pontos medidos e o local de previsão, mas também na disposição espacial geral dos pontos medidos. Para utilizar a disposição espacial nos pesos, a autocorrelação espacial deve ser quantificada. Assim, em kriging comum, o peso, λi, depende de um modelo ajustado aos pontos medidos, da distância até o local de previsão e das relações espaciais entre os valores medidos em torno do local de previsão. As seções seguintes discutem como a fórmula geral de kriging é usada para criar um mapa da superfície de predição e um mapa da precisão das predições.
Tipos de Kriging
Ordinary Kriging
Ordinary kriging assume o modelo
Z(s) = µ + ε(s),
onde µ é uma constante desconhecida. Uma das principais questões relativas ao kriging comum é se a suposição de uma média constante é razoável. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indicator Kriging
Indicator kriging assume o modelo
I(s) = µ + ε(s),
onde µ é uma constante desconhecida e I(s) é uma variável binária. A criação de dados binários pode ser através do uso de um limiar para dados contínuos, ou pode ser que os dados observados sejam 0 ou 1. Por exemplo, você pode ter uma amostra que consiste em informações sobre se um ponto é ou não um habitat florestal ou não florestal, onde a variável binária indica associação de classe. Usando variáveis binárias, o indicador kriging procede da mesma forma que kriging ordinário.
Indicador kriging pode usar semivariogramas ou covariâncias.
Probability Kriging
Probability kriging assume o modelo
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
onde µ1 e µ2 são constantes desconhecidas e I(s) é uma variável binária criada usando um indicador de limiar, I(Z(s) > ct). Note que agora existem dois tipos de erros aleatórios, ε1(s) e ε2(s), portanto há autocorrelação para cada um deles e correlação cruzada entre eles. O kriging de probabilidade se esforça para fazer a mesma coisa que o kriging indicador, mas usa o cokriging na tentativa de fazer um trabalho melhor.
Probability kriging pode usar tanto semivariogramas como covariâncias, cruzamentos e transformações, mas não pode permitir erros de medição.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-slot=”9271753327″>
Disjunctive Kriging
Disjunctive kriging assume o model
f(Z(s)) = µ1 + ε(s),
onde µ1 é uma constante desconhecida e f(Z(s)) é uma função arbitrária de Z(s). Note que você pode escrever f(Z(s)) = I(Z(s) > ct), então o indicador kriging é um caso especial de disjunctive kriging. Em Geostatistical Analyst, você pode prever o valor em si ou um indicador com disjunctive kriging.
Em geral, o kriging disjuntivo tenta fazer mais do que o kriging ordinário. Embora as recompensas possam ser maiores, os custos também o são. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Para ter uma visão profunda sobre a abordagem matemática em Kriging por favor clique em Kriging a Interpolation Method.
PointInterp
Um método semelhante ao IDW, a função PointInterp permite maior controle sobre a vizinhança da amostragem. A influência de uma determinada amostra no valor da célula da grade interpolada depende se o ponto de amostra está na vizinhança cellʼs e a que distância da célula que está sendo interpolada ela está localizada. Pontos fora da vizinhança não têm influência.

PointInterp; Cortesia: ESRI
O valor ponderado dos pontos dentro da vizinhança é calculado usando uma interpolação de distância ponderada inversa ou uma interpolação de distância exponencial inversa. Este método interpola um raster usando características de pontos, mas permite diferentes tipos de vizinhança. As vizinhanças podem ter formas como círculos, rectângulos, polígonos irregulares, anulações ou calços.
Tendência
Tendência é um método estatístico que encontra a superfície que se ajusta aos pontos de amostra usando um ajuste de regressão menos quadrado. Ela se encaixa em uma equação polinomial para toda a superfície. Isto resulta em uma superfície que minimiza a variância da superfície em relação aos valores de entrada. A superfície é construída de modo que para cada ponto de entrada, o total das diferenças entre os valores reais e os valores estimados (isto é, a variância) será o menor possível.
 p>Trend; Courtsey:ESRI
p>Trend; Courtsey:ESRI É um interpolador inexato, e a superfície resultante raramente passa através dos pontos de entrada. Entretanto, este método detecta tendências nos dados da amostra e é similar a fenômenos naturais que tipicamente variam suavemente.
Advantage
- As superfícies de tendência são boas para identificar padrões de escala grosseira nos dados; a superfície interpolada raramente passa através dos pontos de amostra.
Topo to Raster
Ao interpolar valores de elevação para uma raster, o método Topo to Raster impõe restrições que asseguram um modelo de elevação digital hidrologicamente correcto que contém uma estrutura de drenagem conectada e representa correctamente as cristas e riachos a partir dos dados de contorno de entrada. Ele usa uma técnica iterativa de interpolação por diferença finita que otimiza a eficiência computacional da interpolação local sem perder a continuidade superficial da interpolação global. Foi especificamente concebido para trabalhar de forma inteligente com entradas de contorno.
Below é um exemplo de uma superfície interpolada a partir de pontos de elevação, linhas de contorno, linhas de riacho e polígonos lacustres usando interpolação Topo para Raster.
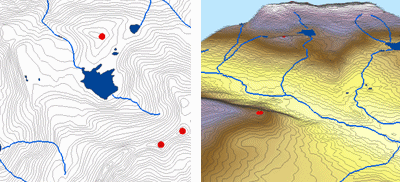
Topo para raster; Cortesia: ESRI
Topo to Raster é uma ferramenta especializada para criar superfícies rasterizadas hidrologicamente correctas a partir de dados vectoriais de componentes do terreno tais como pontos de elevação, linhas de contorno, linhas de riacho, polígonos lacustres, pontos de afundamento, e polígonos de limite de área de estudo.
Densidade
Ferramentas de densidade (disponíveis no ArcGIS) produzem uma superfície que representa o quanto ou quantos de alguma coisa há por unidade de área. A ferramenta Densidade é útil para criar superfícies densas para representar a distribuição de uma população de vida selvagem a partir de um conjunto de observações, ou o grau de urbanização de uma área com base na densidade das estradas.

Density Raster; Courtest: ERSI
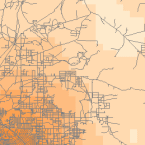
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method