Ce este trucul kernel-ului? De ce este important?
Când se vorbește despre kernel-uri în învățarea automată, cel mai probabil primul lucru care vă vine în minte este modelul mașinilor vectoriale de suport (SVM), deoarece trucul kernel-ului este utilizat pe scară largă în modelul SVM pentru a face legătura între liniaritate și neliniaritate.
Pentru a vă ajuta să înțelegeți ce este un kernel și de ce este important, am să vă prezint mai întâi elementele de bază ale modelului SVM.
Modelul SVM este un model de învățare automată supravegheată care este utilizat în principal pentru clasificări (dar ar putea fi utilizat și pentru regresie!). Acesta învață cum să separe diferite grupuri prin formarea unor limite de decizie.

În graficul de mai sus, observăm că există două clase de observații: punctele albastre și punctele mov. Există o mulțime de modalități de a separa aceste două clase, așa cum se arată în graficul din stânga. Cu toate acestea, dorim să găsim „cel mai bun” hiperplan care ar putea maximiza marja dintre aceste două clase, ceea ce înseamnă că distanța dintre hiperplan și cele mai apropiate puncte de date de pe fiecare parte este cea mai mare. În funcție de care parte a hiperplanului se situează un nou punct de date, am putea atribui o clasă noii observații.
Sună simplu în exemplul de mai sus. Cu toate acestea, nu toate datele sunt liniar separabile. De fapt, în lumea reală, aproape toate datele sunt distribuite aleatoriu, ceea ce face dificilă separarea liniară a diferitelor clase.

De ce este important să folosim trucul kernel?
După cum puteți vedea în imaginea de mai sus, dacă găsim o modalitate de a cartografia datele din spațiul bidimensional în spațiul tridimensional, vom putea găsi o suprafață de decizie care să se împartă clar între diferite clase. Primul meu gând cu privire la acest proces de transformare a datelor este de a cartografia toate punctele de date într-o dimensiune mai mare (în acest caz, 3 dimensiuni), de a găsi granița și de a face clasificarea.
Sună bine. Cu toate acestea, atunci când există din ce în ce mai multe dimensiuni, calculele în acest spațiu devin din ce în ce mai costisitoare. Acesta este momentul în care intervine trucul kernelului. Acesta ne permite să operăm în spațiul original al caracteristicilor fără a calcula coordonatele datelor într-un spațiu dimensional superior.
Să ne uităm la un exemplu:
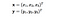
Aici x și y sunt două puncte de date în 3 dimensiuni. Să presupunem că trebuie să cartografiem x și y în spațiul cu 9 dimensiuni. Trebuie să efectuăm următoarele calcule pentru a obține rezultatul final, care este doar un scalar. Complexitatea de calcul, în acest caz, este O(n²).

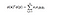
However, if we use the kernel function, which is denoted as k(x, y), instead of doing the complicated computations in the 9-dimensional space, we reach the same result within the 3-dimensional space by calculating the dot product of x -transpose and y. The computational complexity, in this case, is O(n).
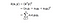
In essence, what the kernel trick does for us is to offer a more efficient and less expensive way to transform data into higher dimensions. With that saying, the application of the kernel trick is not limited to the SVM algorithm. Orice calcule care implică produsele punctiforme (x, y) pot utiliza trucul kernelului.
Diferite funcții kernel
Există diferiți kerneli. Cele mai populare sunt nucleul polinomial și nucleul funcției de bază radială (RBF).
„În mod intuitiv, nucleul polinomial nu se uită doar la caracteristicile date ale eșantioanelor de intrare pentru a determina similitudinea lor, ci și la combinații ale acestora” (Wikipedia), la fel ca în exemplul de mai sus. Cu n caracteristici originale și d grade ale polinomului, nucleul polinomial produce n^d caracteristici extinse.
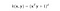
Nucleul RBF se mai numește și nucleul gaussian. Există un număr infinit de dimensiuni în spațiul caracteristic, deoarece acesta poate fi extins cu ajutorul seriei Taylor. În formatul de mai jos, Parametrul γ definește cât de multă influență are un singur exemplu de instruire. Cu cât este mai mare, cu atât mai apropiate trebuie să fie alte exemple pentru a fi influențate (documentația sklearn).
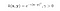
Există diferite opțiuni pentru funcțiile kernel în biblioteca sklearn din Python. Puteți chiar să construiți un kernel personalizat, dacă este necesar.
Finalul
Trucul kernelului sună ca un plan „perfect”. Cu toate acestea, un lucru critic de care trebuie să ținem cont este că, atunci când mapăm datele pe o dimensiune mai mare, există șanse să supraadaptăm modelul. Astfel, alegerea funcției kernel potrivite (inclusiv a parametrilor potriviți) și regularizarea sunt de mare importanță.
Dacă sunteți curioși să aflați ce este regularizarea, am scris un articol în care vorbesc despre modul în care o înțeleg eu și îl puteți găsi aici.
Sper să vă placă acest articol. Ca întotdeauna, vă rog să mă anunțați dacă aveți întrebări, comentarii, sugestii, etc. Mulțumesc pentru lectură 🙂
.