Ce este un filtru trece-jos? Un tutorial despre elementele de bază ale filtrelor RC pasive

decembrie 5, 2021admin

Ce este filtrarea? Aflați ce sunt filtrele trece-jos cu rezistor-capacitor (RC) și unde le puteți utiliza.

Acest articol introduce conceptul de filtrare și explică în detaliu scopul și caracteristicile filtrelor trece-jos cu rezistor-capacitor (RC).

Domeniul timpului și domeniul frecvenței

Când vă uitați la un semnal electric pe un osciloscop, vedeți o linie care reprezintă schimbările de tensiune în raport cu timpul. La orice moment specific în timp, semnalul are o singură valoare de tensiune. Ceea ce vedeți pe osciloscop este reprezentarea în domeniul timpului a semnalului.

O urmă tipică de osciloscop este simplă și intuitivă, dar este, de asemenea, oarecum restrictivă, deoarece nu dezvăluie în mod direct conținutul de frecvență al unui semnal. Spre deosebire de reprezentarea în domeniul timpului, în care un moment în timp corespunde unei singure valori de tensiune, o reprezentare în domeniul frecvenței (denumită și spectru) transmite informații despre un semnal prin identificarea diferitelor componente de frecvență care sunt prezente simultan.

Reprezentări în domeniul temporal ale unei sinusoide (sus) și ale unei unde pătrate (jos).

Reprezentări în domeniul frecvenței ale unei sinusoide (sus) și ale unei unde pătrate (jos).

Ce este un filtru?

Un filtru este un circuit care elimină, sau „filtrează”, o anumită gamă de componente de frecvență. Cu alte cuvinte, acesta separă spectrul semnalului în componente de frecvență care vor fi trecute și componente de frecvență care vor fi blocate.

Dacă nu aveți prea multă experiență cu analiza în domeniul frecvenței, s-ar putea să fiți încă nesigur cu privire la ce sunt aceste componente de frecvență și cum coexistă ele într-un semnal care nu poate avea mai multe valori de tensiune în același timp. Să ne uităm la un scurt exemplu care ne va ajuta să clarificăm acest concept.

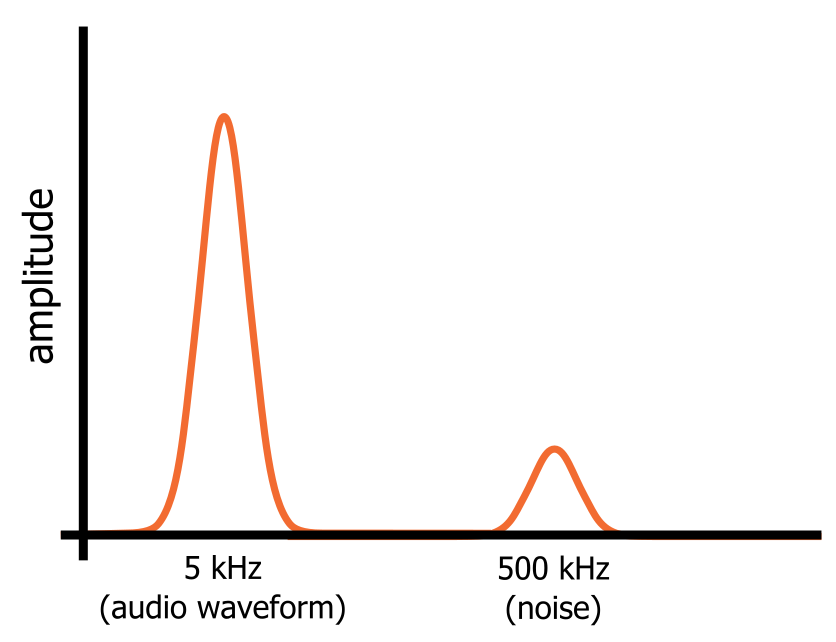
Să ne imaginăm că avem un semnal audio care constă într-o undă sinusoidală perfectă de 5 kHz. Știm cum arată o undă sinusoidală în domeniul timpului, iar în domeniul frecvenței nu vom vedea nimic altceva decât un „vârf” de frecvență la 5 kHz. Acum, să presupunem că activăm un oscilator de 500 kHz care introduce zgomot de înaltă frecvență în semnalul audio.

Semnalul, așa cum este văzut pe un osciloscop, va fi în continuare doar o secvență de tensiuni, cu o valoare pentru fiecare moment de timp, dar semnalul va avea un aspect diferit deoarece variațiile sale în domeniul timpului trebuie să reflecte acum atât unda sinusoidală de 5 kHz, cât și fluctuațiile de zgomot de înaltă frecvență.

În domeniul frecvenței, totuși, unda sinusoidală și zgomotul sunt componente de frecvență separate care sunt prezente simultan în acest semnal unic. Unda sinusoidală și zgomotul ocupă porțiuni diferite ale reprezentării în domeniul de frecvență a semnalului (așa cum se arată în diagrama de mai jos), iar acest lucru înseamnă că putem filtra zgomotul direcționând semnalul printr-un circuit care trece frecvențele joase și blochează frecvențele înalte.

Tipuri de filtre

Filtrele pot fi încadrate în categorii largi care corespund caracteristicilor generale ale răspunsului în frecvență al filtrului. Dacă un filtru trece frecvențele joase și blochează frecvențele înalte, acesta se numește filtru trece-jos. Dacă blochează frecvențele joase și trece frecvențele înalte, este un filtru trece-înalt. Există, de asemenea, filtre trece-bandă, care trec doar o gamă relativ îngustă de frecvențe, și filtre trece-bandă, care blochează doar o gamă relativ îngustă de frecvențe.

Filtrele pot fi, de asemenea, clasificate în funcție de tipurile de componente care sunt utilizate pentru a implementa circuitul. Filtrele pasive utilizează rezistențe, condensatori și inductori; aceste componente nu au capacitatea de a asigura amplificarea și, în consecință, un filtru pasiv poate doar să mențină sau să reducă amplitudinea unui semnal de intrare. Un filtru activ, pe de altă parte, poate atât să filtreze un semnal, cât și să aplice un câștig, deoarece include o componentă activă, cum ar fi un tranzistor sau un amplificator operațional.

Acest filtru activ trece-jos se bazează pe topologia populară Sallen-Key.

Acest articol explorează analiza și proiectarea filtrelor pasive trece-jos. Aceste circuite joacă un rol important într-o mare varietate de sisteme și aplicații.

Filtrul RC trece-jos

Pentru a crea un filtru pasiv trece-jos, trebuie să combinăm un element rezistiv cu un element reactiv. Cu alte cuvinte, avem nevoie de un circuit care constă dintr-un rezistor și fie un condensator, fie un inductor. În teorie, topologia rezistor-inductor (RL) trece-jos este echivalentă, din punct de vedere al capacității de filtrare, cu topologia rezistor-capacitor (RC) trece-jos. În practică, însă, versiunea rezistor-capacitor este mult mai frecventă și, în consecință, restul acestui articol se va concentra pe filtrul trece-jos RC.

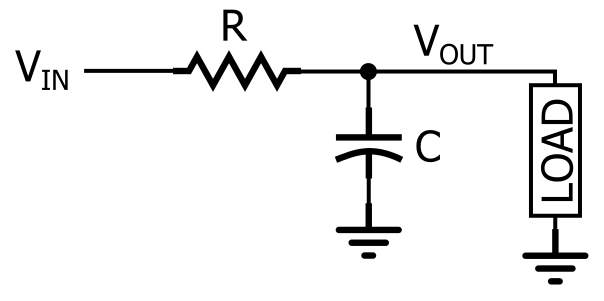
Filtrul trece-jos RC.

După cum puteți vedea în diagramă, un răspuns trece-jos RC este creat prin plasarea unui rezistor în serie cu calea semnalului și a unui condensator în paralel cu sarcina. În diagramă, sarcina este o singură componentă, dar într-un circuit real ar putea fi ceva mult mai complicat, cum ar fi un convertor analog-digital, un amplificator sau etajul de intrare al osciloscopului pe care îl folosiți pentru a măsura răspunsul filtrului.

Putem analiza intuitiv acțiunea de filtrare a topologiei RC low-pass dacă recunoaștem că rezistorul și condensatorul formează un divizor de tensiune dependent de frecvență.

Filtrul RC low-pass redesenat astfel încât să arate ca un divizor de tensiune.

Când frecvența semnalului de intrare este joasă, impedanța condensatorului este mare în raport cu impedanța rezistorului; astfel, cea mai mare parte a tensiunii de intrare este căzută prin condensator (și prin sarcină, care este în paralel cu condensatorul). Atunci când frecvența de intrare este ridicată, impedanța condensatorului este scăzută în raport cu impedanța rezistorului, ceea ce înseamnă că mai multă tensiune este căzută pe rezistor și mai puțină este transferată la sarcină. Astfel, frecvențele joase sunt trecute și frecvențele înalte sunt blocate.

Această explicație calitativă a funcționalității RC low-pass este un prim pas important, dar nu este foarte utilă atunci când trebuie să proiectăm efectiv un circuit, deoarece termenii „frecvență înaltă” și „frecvență joasă” sunt extrem de vagi. Inginerii trebuie să creeze circuite care să treacă și să blocheze frecvențe specifice. De exemplu, în sistemul audio descris mai sus, dorim să păstrăm un semnal de 5 kHz și să suprimăm un semnal de 500 kHz. Acest lucru înseamnă că avem nevoie de un filtru care să treacă de la trecere la blocare undeva între 5 kHz și 500 kHz.

Frecvența de tăiere

Legătura de frecvențe pentru care un filtru nu provoacă o atenuare semnificativă se numește bandă de trecere, iar gama de frecvențe pentru care filtrul provoacă o atenuare semnificativă se numește bandă de oprire. Filtrele analogice, cum ar fi filtrul RC low-pass, trec întotdeauna treptat de la banda de trecere la banda de oprire. Acest lucru înseamnă că este imposibil să se identifice o frecvență la care filtrul nu mai lasă să treacă semnale și începe să le blocheze. Cu toate acestea, inginerii au nevoie de o modalitate de a rezuma în mod convenabil și concis răspunsul în frecvență al unui filtru, și aici intervine conceptul de frecvență de tăiere.

Când vă uitați la un grafic al răspunsului în frecvență al unui filtru RC, veți observa că termenul „frecvență de tăiere” nu este foarte precis. Imaginea în care spectrul unui semnal este „tăiat” în două jumătăți, din care una este reținută și una este eliminată, nu se aplică, deoarece atenuarea crește treptat pe măsură ce frecvențele se deplasează de la sub cutoff la peste cutoff.

Frecvența de cutoff a unui filtru RC trece-jos este de fapt frecvența la care amplitudinea semnalului de intrare este redusă cu 3 dB (această valoare a fost aleasă deoarece o reducere de 3 dB a amplitudinii corespunde unei reduceri de 50% a puterii). Astfel, frecvența de tăiere se mai numește și frecvența de -3 dB și, de fapt, această denumire este mai precisă și mai informativă. Termenul de lățime de bandă se referă la lățimea benzii de trecere a unui filtru, iar în cazul unui filtru trece-jos, lățimea de bandă este egală cu frecvența de -3 dB (așa cum se arată în diagrama de mai jos).

Această diagramă transmite caracteristicile generice ale răspunsului în frecvență al unui filtru trece-jos RC. Lățimea de bandă este egală cu frecvența de -3 dB.

După cum s-a explicat mai sus, comportamentul trece-jos al unui filtru RC este cauzat de interacțiunea dintre impedanța independentă de frecvență a rezistorului și impedanța dependentă de frecvență a condensatorului. Pentru a determina detaliile răspunsului în frecvență al unui filtru, trebuie să analizăm matematic relația dintre rezistență (R) și capacitate (C) și, de asemenea, putem manipula aceste valori pentru a proiecta un filtru care să îndeplinească specificații precise. Frecvența de tăiere (fC) a unui filtru RC trece-jos se calculează după cum urmează:

Să analizăm un exemplu simplu de proiectare. Valorile condensatoarelor sunt mai restrictive decât cele ale rezistențelor, așa că vom începe cu o valoare obișnuită a capacității (cum ar fi 10 nF), iar apoi vom folosi ecuația pentru a determina valoarea necesară a rezistenței. Scopul este de a proiecta un filtru care va păstra o formă de undă audio de 5 kHz și va respinge o formă de undă de zgomot de 500 kHz. Vom încerca o frecvență de tăiere de 100 kHz, iar mai târziu în articol vom analiza mai atent efectul acestui filtru asupra celor două componente de frecvență.

Așadar, o rezistență de 160 Ω combinată cu un condensator de 10 nF ne va oferi un filtru care se apropie foarte mult de răspunsul în frecvență dorit.

Calcularea răspunsului filtrului

Potem calcula comportamentul teoretic al unui filtru trece-jos folosind o versiune dependentă de frecvență a unui calcul tipic de divizor de tensiune. Ieșirea unui divizor de tensiune rezistiv se exprimă astfel:

Filtrul RC folosește o structură echivalentă, dar în locul lui R2 avem un condensator. În primul rând, înlocuim R2 (la numărător) cu reactanța condensatorului (XC). Apoi, trebuie să calculăm magnitudinea impedanței totale și să o plasăm la numitor. Astfel, avem

Reactanța unui condensator indică valoarea opoziției la fluxul de curent, dar, spre deosebire de rezistență, valoarea opoziției depinde de frecvența semnalului care trece prin condensator. Astfel, trebuie să calculăm reactanța la o anumită frecvență, iar ecuația pe care o folosim pentru aceasta este următoarea:

În exemplul de proiectare de mai sus, R ≈ 160 Ω și C = 10 nF. Vom presupune că amplitudinea lui VIN este de 1 V, astfel încât să putem elimina pur și simplu VIN din calcul. Mai întâi să calculăm amplitudinea lui VOUT la frecvența undei sinusoidale:

Amplitudinea undei sinusoidale este în esență neschimbată. Acest lucru este bun, deoarece intenția noastră a fost de a păstra unda sinusoidală, suprimând în același timp zgomotul. Acest rezultat nu este surprinzător, deoarece am ales o frecvență de tăiere (100 kHz) care este mult mai mare decât frecvența undei sinusoidale (5 kHz).

Acum să vedem cu cât succes va atenua filtrul componenta de zgomot.

Amplitudinea zgomotului este de numai aproximativ 20% din valoarea sa inițială.

Vizualizarea răspunsului filtrului

Mediul cel mai convenabil de evaluare a efectului unui filtru asupra unui semnal este de a examina un grafic al răspunsului în frecvență al filtrului. Aceste grafice, adesea numite diagrame Bode, au magnitudinea (în decibeli) pe axa verticală și frecvența pe axa orizontală; axa orizontală are de obicei o scară logaritmică, astfel încât distanța fizică dintre 1 Hz și 10 Hz este aceeași cu distanța fizică dintre 10 Hz și 100 Hz, dintre 100 Hz și 1 kHz și așa mai departe. Această configurație ne permite să evaluăm rapid și cu precizie comportamentul unui filtru pe o gamă foarte mare de frecvențe.

Un exemplu de grafic de răspuns în frecvență.

Care punct de pe curbă indică magnitudinea pe care o va avea semnalul de ieșire dacă semnalul de intrare are o magnitudine de 1 V și o frecvență egală cu valoarea corespunzătoare de pe axa orizontală. De exemplu, atunci când frecvența de intrare este de 1 MHz, amplitudinea de ieșire (presupunând o amplitudine de intrare de 1 V) va fi de 0,1 V (deoarece -20 dB corespunde unei reduceri de un factor de zece).

Forma generală a acestei curbe frecvență-răspuns va deveni foarte familiară pe măsură ce veți petrece mai mult timp cu circuitele de filtrare. Curba este aproape perfect plană în banda de trecere, iar apoi începe să scadă mai rapid pe măsură ce frecvența de intrare se apropie de frecvența de cutoff. În cele din urmă, rata de variație a atenuării, numită roll-off, se stabilizează la 20 dB/decadă – adică, magnitudinea semnalului de ieșire este redusă cu 20 dB pentru fiecare creștere de zece ori mai mare a frecvenței de intrare.

Evaluarea performanței filtrului trece-jos

Dacă trasăm cu atenție răspunsul în frecvență al filtrului pe care l-am proiectat mai devreme în articol, vom vedea că răspunsul în magnitudine la 5 kHz este în esență de 0 dB (i.e, o atenuare aproape nulă), iar răspunsul de amplitudine la 500 kHz este de aproximativ -14 dB (ceea ce corespunde unui câștig de 0,2). Aceste valori sunt în concordanță cu rezultatele calculelor pe care le-am efectuat în secțiunea anterioară.

Pentru că filtrele RC au întotdeauna o tranziție treptată de la banda de trecere la banda de oprire și pentru că atenuarea nu ajunge niciodată la infinit, nu putem proiecta un filtru „perfect” – adică un filtru care nu are niciun efect asupra undei sinusoidale și care elimină complet zgomotul. În schimb, avem întotdeauna un compromis. Dacă mutăm frecvența de tăiere mai aproape de 5 kHz, vom avea o atenuare mai mare a zgomotului, dar și o atenuare mai mare a undei sinusoidale pe care dorim să o trimitem la un difuzor. Dacă mutăm frecvența de tăiere mai aproape de 500 kHz, vom avea mai puțină atenuare la frecvența undei sinusoidale, dar și mai puțină atenuare la frecvența zgomotului.

Deplasarea de fază a filtrului trece-jos

Până acum am discutat despre modul în care un filtru modifică amplitudinea diferitelor componente de frecvență dintr-un semnal. Cu toate acestea, elementele reactive ale circuitului introduc întotdeauna deplasarea de fază în plus față de efectele de amplitudine.

Conceptul de fază se referă la valoarea unui semnal periodic la un anumit moment în cadrul unui ciclu. Astfel, atunci când spunem că un circuit provoacă defazaj, ne referim la faptul că acesta creează o nepotrivire între semnalul de intrare și semnalul de ieșire: semnalele de intrare și de ieșire nu-și mai încep și nu-și mai termină ciclurile la același moment în timp. Valoarea decalajului de fază, cum ar fi 45° sau 90°, indică cât de mult a fost creat decalajul.

Care element reactiv dintr-un circuit introduce un decalaj de fază de 90°, dar acest decalaj de fază nu se produce dintr-o dată. Faza semnalului de ieșire, la fel ca și magnitudinea semnalului de ieșire, se modifică treptat pe măsură ce crește frecvența de intrare. Într-un filtru trece-jos RC, avem un singur element reactiv (condensatorul) și, în consecință, circuitul va introduce în cele din urmă o defazaj de 90°.

Ca și în cazul răspunsului la magnitudine, răspunsul la fază este cel mai ușor de evaluat prin examinarea unui grafic în care axa orizontală indică frecvența logaritmică. Descrierea de mai jos transmite tiparul general, iar apoi puteți completa detaliile examinând graficul.

Deplasarea de fază este inițial de 0°.
Crește treptat până când ajunge la 45° la frecvența de tăiere; în timpul acestei porțiuni a răspunsului, rata de schimbare este în creștere.
După frecvența de tăiere, defazajul continuă să crească, dar rata de variație este în scădere.
Rata de variație devine foarte mică pe măsură ce defazajul se apropie asimptotic de 90°.

Linia continuă este răspunsul în mărime, iar linia punctată este răspunsul în fază. Frecvența de cutoff este de 100 kHz. Observați că defazajul este de 45° la frecvența de tăiere.

Filtre trece-jos de ordinul doi

Până acum am presupus că un filtru trece-jos RC este format dintr-un rezistor și un condensator. Această configurație este un filtru de ordinul întâi.

„Ordinul” unui filtru pasiv este determinat de numărul de elemente reactive – de exemplu, condensatori sau inductori – care sunt prezente în circuit. Un filtru de ordin mai mare are mai multe elemente reactive, iar acest lucru duce la un defazaj mai mare și o atenuare mai abruptă. Această a doua caracteristică este motivația principală pentru creșterea ordinului unui filtru.

Prin adăugarea unui element reactiv la un filtru – de exemplu, trecând de la ordinul întâi la ordinul al doilea sau de la ordinul al doilea la ordinul al treilea – creștem reducerea maximă cu 20 dB/decadă. O atenuare mai abruptă se traduce printr-o tranziție mai rapidă de la o atenuare scăzută la o atenuare ridicată, iar acest lucru poate duce la o performanță îmbunătățită atunci când semnalul nu are o bandă de frecvență largă care să separe componentele de frecvență dorite de componentele de zgomot.

Filtrele de ordinul doi sunt în mod obișnuit construite în jurul unui circuit rezonant format dintr-un inductor și un condensator (această topologie se numește „RLC” pentru rezistență-inductor-capacitor). Cu toate acestea, este de asemenea posibil să se creeze filtre RC de ordinul al doilea. După cum se arată în diagrama de mai jos, tot ce trebuie să facem este să punem în cascadă două filtre RC de ordinul întâi.

Chiar dacă această topologie creează cu siguranță un răspuns de ordinul al doilea, ea nu este utilizată pe scară largă – după cum vom vedea în secțiunea următoare, răspunsul în frecvență este adesea inferior celui al unui filtru activ de ordinul al doilea sau al unui filtru RLC de ordinul al doilea.

Răspunsul în frecvență al filtrului RC de ordinul al doilea

Potem încerca să creăm un filtru RC trece-jos de ordinul al doilea prin proiectarea unui filtru de ordinul întâi în funcție de frecvența de tăiere dorită și apoi prin conectarea în serie a două dintre aceste etaje de ordinul întâi. Acest lucru are ca rezultat un filtru care are un răspuns în frecvență global similar și un roll-off maxim de 40 dB/decadă în loc de 20 dB/decadă.

Cu toate acestea, dacă ne uităm mai atent la răspuns, observăm că frecvența de -3 dB a scăzut. Filtrul RC de ordinul al doilea nu se comportă așa cum era de așteptat deoarece cele două etaje nu sunt independente – nu putem conecta pur și simplu aceste două etaje împreună și să analizăm circuitul ca un filtru trece-jos de ordinul întâi urmat de un filtru trece-jos de ordinul întâi identic.

În plus, chiar dacă introducem un tampon între cele două etaje, astfel încât primul etaj RC și al doilea etaj RC să poată funcționa ca filtre independente, atenuarea la frecvența de tăiere originală va fi de 6 dB în loc de 3 dB. Acest lucru se întâmplă tocmai pentru că cele două etape funcționează independent – primul filtru are o atenuare de 3 dB la frecvența de tăiere, iar al doilea filtru adaugă încă 3 dB de atenuare.

Limitarea fundamentală a filtrului trece-jos RC de ordinul al doilea este că proiectantul nu poate regla fin tranziția de la banda de trecere la banda de oprire prin ajustarea factorului Q al filtrului; acest parametru indică cât de amortizat este răspunsul în frecvență. Dacă puneți în cascadă două filtre RC low-pass identice, funcția de transfer globală corespunde unui răspuns de ordinul doi, dar factorul Q este întotdeauna 0,5. Atunci când Q = 0,5, filtrul se află la limita supraamorsării, ceea ce are ca rezultat un răspuns în frecvență care se „curbează” în regiunea de tranziție. Filtrele active de ordinul al doilea și filtrele bazate pe rezonanță de ordinul al doilea nu au această limitare; proiectantul poate controla factorul Q și, astfel, poate regla cu precizie răspunsul în frecvență în regiunea de tranziție.

Rezumat

Toate semnalele electrice conțin un amestec de componente de frecvență dorite și componente de frecvență nedorite. Componentele de frecvență nedorite sunt de obicei cauzate de zgomot și interferențe și, în unele situații, acestea vor afecta în mod negativ performanța sistemului.
Un filtru este un circuit care reacționează în moduri diferite la diferite porțiuni din spectrul unui semnal. Un filtru trece-jos este proiectat să treacă componentele de joasă frecvență și să blocheze componentele de înaltă frecvență.
Frecvența de tăiere a unui filtru trece-jos indică regiunea de frecvență în care filtrul trece de la o atenuare scăzută la o atenuare semnificativă.
Tensiunea de ieșire a unui filtru RC trece-jos poate fi calculată prin tratarea circuitului ca un divizor de tensiune format dintr-o rezistență (independentă de frecvență) și o reactanță (dependentă de frecvență).
Un grafic al magnitudinii (în dB, pe axa verticală) în funcție de frecvența logaritmică (în hertzi, pe axa orizontală) este o modalitate convenabilă și eficientă de a examina comportamentul teoretic al unui filtru. De asemenea, puteți utiliza o diagramă a fazei în funcție de frecvența logaritmică pentru a determina valoarea defazării care va fi aplicată unui semnal de intrare.
Un filtru de ordinul al doilea oferă un roll-off mai abrupt; acest răspuns de ordinul al doilea este util atunci când un semnal nu oferă o bandă largă de separare între componentele de frecvență dorite și componentele de frecvență nedorite.
Puteți crea un filtru RC trece-jos de ordinul al doilea prin construirea a două filtre RC trece-jos identice de ordinul întâi și apoi prin conectarea ieșirii unuia la intrarea celuilalt. Frecvența globală de -3 dB va fi mai mică decât era de așteptat.