dB: Ce este un decibel?

Presiunea sonoră, nivelul sonor și dB. Sunetul se măsoară, de obicei, cu ajutorul microfoanelor, iar acestea răspund proporțional cu presiunea sonoră, p. Acum, puterea dintr-o undă sonoră, toate celelalte fiind egale, merge ca pătratul presiunii. (În mod similar, puterea electrică într-un rezistor este egală cu pătratul tensiunii). Loganul lui x2 este doar 2 log x, astfel încât acest lucru introduce un factor de 2 atunci când convertim rapoartele de presiune în decibeli. Diferența de nivel de presiune acustică între două sunete cu p1 și p2 este, prin urmare:

20 log (p2/p1) dB = 10 log (p22/p12) dB = 10 log (P2/P1) dB (peste tot, logul este în baza 10).

Ce se întâmplă când înjumătățim puterea sunetului? Loganul lui 2 este 0,3010, deci loganul lui 1/2 este -0,3, cu o bună aproximație. Așadar, dacă înjumătățiți puterea, reduceți puterea și nivelul sonor cu 3 dB. Înjumătățiți-o din nou (până la 1/4 din puterea inițială) și reduceți nivelul cu încă 3 dB. Dacă continuați să înjumătățiți puterea, veți avea aceste rapoarte.

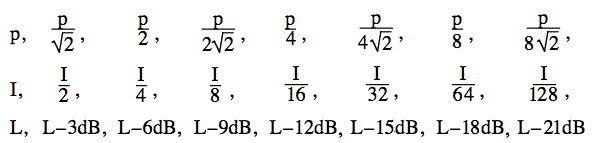
Ce se întâmplă dacă adaug două sunete identice? Dublez intensitatea (creștere de 3 dB)? Sau dublez presiunea (creștere de 6 dB)? Această întrebare frecventă este puțin subtilă, așa că este discutată aici, în FAQ.

Filiere sonore pentru a arăta mărimea unui decibel

Am văzut mai sus că înjumătățirea puterii reduce presiunea sonoră cu √2 și nivelul sonor cu 3 dB. Aceasta este ceea ce am făcut în primul grafic și în fișierul sonor de mai jos.

Primul eșantion de sunet este un zgomot alb (un amestec al unei game largi de frecvențe audibile, analog cu lumina albă, care este un amestec al tuturor frecvențelor vizibile). Al doilea eșantion este același zgomot, cu tensiunea redusă cu un factor de √2. Acum 1/√2 este de aproximativ 0,7, astfel încât -3 dB corespunde reducerii tensiunii sau presiunii la 70% din valoarea sa inițială. Linia verde arată tensiunea în funcție de timp. Linia roșie arată o descreștere exponențială continuă în funcție de timp. Observați că tensiunea scade cu 50% pentru fiecare al doilea eșantion.

Observați, de asemenea, că o dublare a puterii nu face o diferență uriașă în ceea ce privește intensitatea sonoră. Vom discuta acest lucru în continuare mai jos, dar este un lucru util de reținut atunci când alegeți un echipament de reproducere a sunetului.

File de sunet și animație de John Tann și George Hatsidimitris.

Cât de mare este un decibel? În următoarea serie, eșantioanele succesive sunt reduse cu doar un decibel.

Un decibel este de același ordin ca și diferența doar sesizabilă (JND) pentru nivelul sonor. Pe măsură ce ascultați aceste fișiere, veți observa că ultimul este mai silențios decât primul, dar este destul de puțin clar pentru ureche că al doilea din orice pereche este mai silențios decât predecesorul său. 10*log10(1,26) = 1, deci pentru a crește nivelul sonor cu 1 dB, puterea trebuie să crească cu 26% sau tensiunea cu 12%.

Ce se întâmplă dacă diferența este mai mică de un decibel? Nivelurile sonore sunt rareori indicate cu zecimale. Motivul este că nivelurile sonore care diferă cu mai puțin de 1 dB sunt greu de distins, după cum arată următorul exemplu. (Acest lucru face ca dB să fie o unitate de mărime convenabilă.)

	Pași de 0,3 dB. Este posibil să observați că ultima este mai silențioasă decât prima, dar este dificil să observați diferența între perechile succesive. 10*log10(1,07) = 0,3, deci pentru a crește nivelul sonor cu 0,3 dB, puterea trebuie crescută cu 7%, sau tensiunea cu 3,5%.

Niveluri standard de referință (nivel sonor „absolut”)

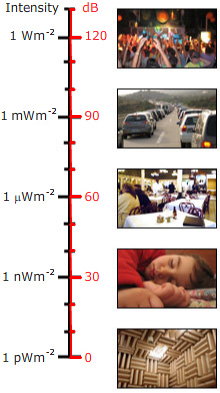Am spus mai sus că decibelul este un raport. Astfel, atunci când este utilizat pentru a da nivelul sonor pentru un singur sunet, mai degrabă decât un raport, trebuie ales un nivel de referință. Pentru nivelul de presiune acustică, nivelul de referință (pentru aer) este de obicei ales ca fiind pref = 20 micropascali (20 μPa), sau 0,02 mPa. Acest nivel este foarte scăzut: este de 2 zecimi de miliardime dintr-o atmosferă. Cu toate acestea, aceasta este aproximativ limita de sensibilitate a urechii umane, în domeniul său sensibil de frecvență. (De obicei, această sensibilitate se întâlnește doar la persoanele destul de tinere sau la persoanele care nu au fost expuse la muzică tare sau la alte zgomote puternice. Sistemele muzicale personale cu difuzoare intraauriculare sunt capabile să atingă niveluri sonore foarte ridicate în ureche și sunt considerate de unii ca fiind responsabile pentru o mare parte din pierderea auzului la adulții tineri din unele țări).

Așa că, dacă citiți despre un nivel de presiune acustică de 86 dB, înseamnă că

20 log (p2/pref) = 86 dB

unde pref este presiunea acustică a nivelului de referință, iar p2 cea a sunetului în cauză. Împărțiți ambele părți la 20:

log (p2/pref) = 4,3

p>2/pref = 104,3

4 este logaritmul a 10 mii, 0,3 este logaritmul a 2, deci acest sunet are o presiune sonoră de 20 de mii de ori mai mare decât cea a nivelului de referință (p2/pref = 20.000) sau o intensitate de 400 de milioane de ori mai mare decât intensitatea de referință. 86 dB este un sunet puternic, dar nu este periculos – cu condiția ca expunerea să fie scurtă.

Ce înseamnă 0 dB? Acest nivel apare atunci când intensitatea măsurată este egală cu nivelul de referință. de exemplu, este nivelul sonor corespunzător la 0,02 mPa. În acest caz avem

nivelul sonor = 20 log (pmăsurat/pref) = 20 log 1 = 0 dB

Rețineți că decibelii măsoară un raport. 0 dB apare atunci când se ia logaritmul unui raport de 1 (log 1 = 0). Așadar, 0 dB nu înseamnă absența sunetului, ci un nivel sonor în care presiunea sonoră este egală cu cea a nivelului de referință. Aceasta este o presiune mică, dar nu zero. De asemenea, este posibil să existe niveluri sonore negative: – 20 dB ar însemna un sunet cu o presiune de 10 ori mai mică decât presiunea de referință, adică 2 μPa.

Nu toate presiunile sonore sunt la fel de puternice. Acest lucru se datorează faptului că urechea umană nu răspunde în mod egal la toate frecvențele: suntem mult mai sensibili la sunetele din intervalul de frecvență cuprins între aproximativ 1 kHz și 7 kHz (între 1000 și 7000 de vibrații pe secundă) decât la sunetele de frecvență foarte joasă sau înaltă. Din acest motiv, sonometrele sunt, de obicei, echipate cu un filtru al cărui răspuns la frecvență este puțin asemănător cu cel al urechii umane. (Mai multe despre aceste filtre mai jos.) Dacă se utilizează „filtrul de ponderare A”, nivelul de presiune acustică este dat în unități de dB(A) sau dBA. Nivelul presiunii sonore pe scara dBA este ușor de măsurat și, prin urmare, este utilizat pe scară largă. Unul dintre motivele pentru care este diferit de intensitatea sonoră este faptul că filtrul nu răspunde în același mod ca și urechea. Pentru a înțelege intensitatea sonoră a unui sunet, primul lucru pe care trebuie să-l faceți este să consultați câteva curbe reprezentând răspunsul în frecvență al urechii umane, prezentate mai jos. (Alternativ, vă puteți măsura propriul răspuns auditiv.) Un alt motiv este că auzul uman nu este logaritmic.

Măsuri logaritmice

De ce folosim decibeli? Urechea este capabilă să audă o gamă foarte mare de sunete: raportul dintre presiunea sonoră care provoacă daune permanente în urma unei expuneri scurte și limita pe care urechile (nedeteriorate) o pot auzi este mai mare de un milion. Pentru a face față unei astfel de game, sunt utile unitățile logaritmice: logaritmul unui milion este 6, deci acest raport reprezintă o diferență de 120 dB. Auzul nu are un răspuns logaritmic în mod inerent. (Măsurile logaritmice sunt, de asemenea, utile atunci când un sunet (pentru scurt timp) crește sau scade exponențial în timp. Acest lucru se întâmplă în multe aplicații care implică un câștig proporțional sau o pierdere proporțională.)

Filtrele utilizate pentru dBA și dB(C)

Cel mai utilizat filtru de nivel sonor este scara A, care corespunde aproximativ inversului curbei de zgomot egal de 40 dB (la 1 kHz). Utilizând acest filtru, sonometrul este astfel mai puțin sensibil la frecvențele foarte înalte și foarte joase. Măsurătorile efectuate pe această scală sunt exprimate în dBA. Scara C variază puțin pe mai multe octave și, prin urmare, este potrivită pentru măsurători subiective numai pentru niveluri sonore moderate și înalte. Măsurătorile efectuate pe această scală sunt exprimate în dB(C). Există, de asemenea, o scală de ponderare B (rar utilizată), intermediară între A și C. Figura de mai jos prezintă răspunsul filtrului A (stânga) și al filtrului C, cu câștiguri în dB date în raport cu 1 kHz. (Pentru o introducere în filtre, consultați Filtre RC, integratoare și diferențiatoare).



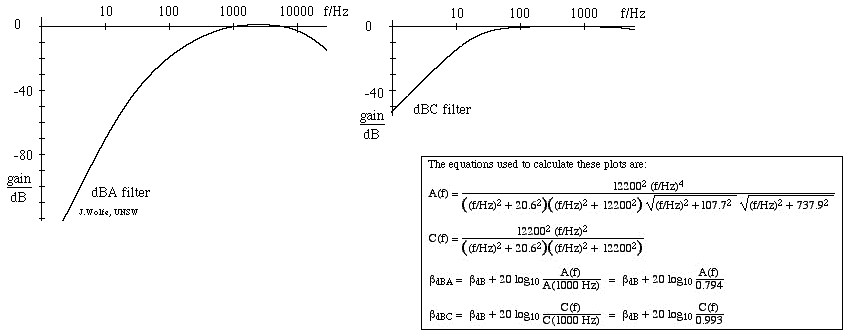
Pe site-urile de acustică muzicală și de acustică vocală, se trasează spectrele sonore în dB. Motivul pentru această practică obișnuită este faptul că gama de presiuni sonore măsurate este mare.

Măsurătorile dB(G) utilizează un filtru de bandă îngustă care acordă o pondere mare frecvențelor cuprinse între 1 și 20 Hz și o pondere mică celorlalte. Astfel, acesta oferă valori mari pentru sunete și infrasunete care nu pot fi auzite cu ușurință. ISO 7196:1995

Loudness, phons și sones, curbe de răspuns auditiv

Phon-ul este o unitate care se raportează la dB prin răspunsul în frecvență măsurat psihofizic al urechii. La 1 kHz, citirile în phons și dB sunt, prin definiție, identice. Pentru toate celelalte frecvențe, scara phon este determinată de rezultatele experimentelor în care voluntarilor li s-a cerut să ajusteze intensitatea unui semnal la o anumită frecvență până când au considerat că intensitatea sa este egală cu cea a unui semnal de 1 kHz. Pentru a converti din dB în phon, aveți nevoie de un grafic al acestor rezultate. Un astfel de grafic depinde de nivelul sonor: acesta devine mai plat la niveluri sonore ridicate.

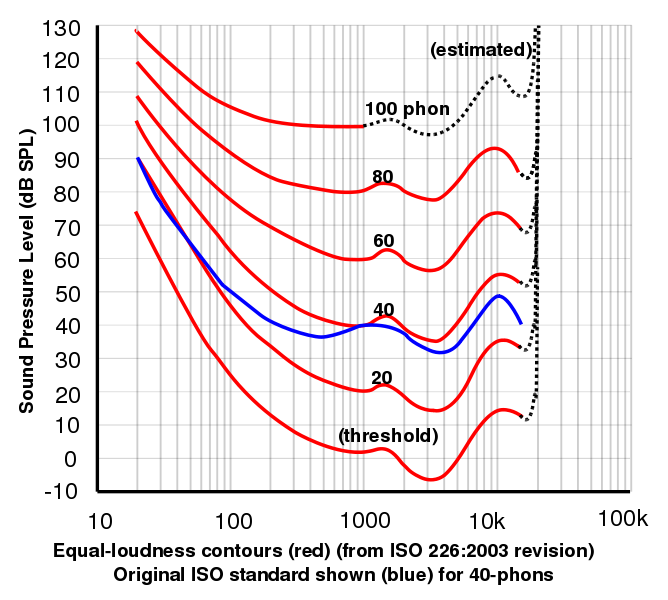
Acest grafic, oferit de Lindosland, prezintă datele din 2003 ale Organizației Internaționale de Standardizare pentru curbele de intensitate sonoră egală determinate experimental. Graficele de intensitate sonoră egală în funcție de frecvență sunt adesea denumite generic curbe Fletcher-Munson, după lucrarea originală a lui Fletcher, H. și Munson, W.A. (1933) J.Acoust.Soc.Am. 6:59. Puteți să vă faceți propriile curbe folosind site-ul nostru de răspuns auditiv.

Sonorul este derivat din măsurători psihofizice care au implicat voluntari care au ajustat sunetele până când le-au judecat ca fiind de două ori mai puternice. Acest lucru permite să se raporteze intensitatea sonoră percepută la phon. Un sone este definit ca fiind egal cu 40 de phoni. În mod experimental, s-a constatat că, peste 40 de foni, o creștere de 10 dB a nivelului sonor corespunde aproximativ unei dublări a intensității percepute. Astfel, această aproximație este utilizată în definirea sonei: 1 sone = 40 phon, 2 sone = 50 phon, 4 sone = 60 phon, etc.



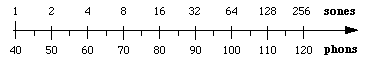
Această relație implică faptul că intensitatea sonoră și intensitatea sunt legate printr-o lege de putere: intensitatea sonoră în sone este proporțională cu (intensitate)log 2 = (intensitate)0,3.

Nu ar fi grozav să putem converti din dB (care poate fi măsurat cu un instrument) în sone (care aproximează intensitatea sonoră așa cum este percepută de oameni)? Acest lucru se face uneori cu ajutorul unor tabele pe care le puteți găsi în manualele de acustică. Cu toate acestea, dacă nu vă deranjează o aproximare destul de rudimentară, puteți spune că curba de ponderare A aproximează răspunsul în frecvență al omului la niveluri sonore joase și moderate, astfel încât dB(A) este foarte aproximativ același lucru cu fonii, pe o gamă limitată de niveluri joase. Apoi, se poate folosi relația logaritmică dintre sone și phons descrisă mai sus.

Nivelul de înregistrare și decibelii

Măsurătoarele care măsoară nivelul de înregistrare sau de ieșire pe echipamentele electronice audio (console de mixaj etc.) înregistrează aproape întotdeauna tensiunea AC rms (a se vedea linkurile pentru a afla mai multe despre AC și rms). Pentru o anumită rezistență R, puterea P este V2/R, deci
diferența nivelului de tensiune = 20 log (V2/V1) dB = 10 log (V22/V12) dB = 10 log (P2/P1) dB, sau

nivelul absolut de tensiune = 20 log (V/Vref)

unde Vref este o tensiune de referință. Așadar, care este tensiunea de referință?

Nivelul evident de ales este un volt rms, iar în acest caz nivelul este scris ca dBV. Acest lucru este rațional și, de asemenea, convenabil cu cardurile analog-digitale a căror gamă maximă este adesea de aproximativ un volt rms. Așadar, trebuie să ne amintim să menținem nivelul în dBV negativ (mai puțin de un volt) pentru a evita tăierea vârfurilor semnalului, dar nu prea negativ (astfel încât semnalul dvs. să fie totuși mult mai mare decât zgomotul de fond).

Câteodată veți vedea dBm. Acest lucru obișnuia să însemne decibeli de putere electrică, în raport cu un miliwatt, și uneori încă mai înseamnă asta. Cu toate acestea, este complicat din motive istorice. La mijlocul secolului al XX-lea, multe linii audio aveau o impedanță nominală de 600 Ω. Dacă impedanța este pur rezistivă și dacă setați V2/600 Ω = 1 mW, atunci veți obține V = 0,775 volți. Așadar, cu condiția să folosiți o sarcină de 600 Ω, 1 mW de putere era 0 dBm, ceea ce înseamnă 0,775 V, așa că ați calibrat astfel apometrele de nivel. Problema a apărut deoarece, odată ce un nivelmetru care măsoară tensiunea este calibrat astfel, acesta va citi 0 dBm la 0,775 V chiar dacă nu este conectat la 600 Ω Deci, poate ilogic, dBm va însemna uneori dB în raport cu 0,775 V. (Când eram copil, calculatoarele erau scumpe, așa că foloseam vechea riglă de calcul a tatei, care avea factorul 0,775 marcat pe fereastra cursorului pentru a facilita astfel de calcule).

Cum se convertește dBV sau dBm în dB de nivel sonor? Nu există o modalitate simplă. Depinde de modul în care convertiți puterea electrică în putere sonoră. Chiar dacă semnalul electric este conectat direct la un difuzor, conversia va depinde de eficiența și impedanța difuzorului dumneavoastră. Și, bineînțeles, poate exista un amplificator de putere și diverse complicații acustice între locul în care măsurați dBV pe pupitrul de mixaj și locul în care se află urechile dumneavoastră în câmpul sonor.

Intensitate, radiație și dB

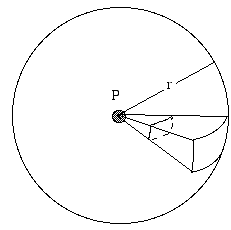
Cum depinde nivelul sunetului (sau nivelul semnalului radio, etc.) de distanța față de sursă?

O sursă care emite radiații în mod egal în toate direcțiile se numește izotropă. Luați în considerare o sursă izolată de sunet, departe de orice suprafață reflectantă – poate o pasăre care cântă la înălțime. Imaginați-vă o sferă cu raza r, centrată pe sursă. Sursa emite o putere totală P, în mod continuu. Această putere sonoră se răspândește și trece prin suprafața sferei. Dacă sursa este izotropă, intensitatea I este aceeași peste tot pe această suprafață, prin definiție. Intensitatea I este definită ca fiind puterea pe unitatea de suprafață. Aria suprafeței sferei este de 4πr2, astfel încât puterea (în exemplul nostru, puterea sunetului) care trece prin fiecare metru pătrat de suprafață este, prin definiție:

I = P/4πr2.

Deci vedem că, pentru o sursă izotropă, intensitatea este invers proporțională cu pătratul distanței de la sursă:

I2/I1 = r12/r22.

Dar intensitatea este proporțională cu pătratul presiunii sonore, așa că am putea scrie la fel de bine:

p2/p1 = r1/r2.

Atunci, dacă dublăm distanța, reducem presiunea sonoră cu un factor 2 și intensitatea cu un factor 4: cu alte cuvinte, reducem nivelul sonor cu 6 dB. Dacă mărim r cu un factor de 10, reducem nivelul cu 20 dB, etc.

Atenție, însă, că multe surse nu sunt izotrope, mai ales dacă lungimea de undă este mai mică sau de o mărime comparabilă cu cea a sursei. Mai mult, reflexiile sunt adesea destul de importante, mai ales dacă solul este în apropiere sau dacă vă aflați în interior.

Presiunea, intensitatea și impedanța specifică

Pentru undele acustice, impedanța acustică specifică z este definită ca fiind raportul dintre presiunea acustică p și viteza medie a particulelor u, datorată ave sunetului, z = p/u . În Impedanța acustică, intensitatea și puterea acustică, arătăm cum se raportează presiunea acustică RMS p și intensitatea I:
I = p2/z

Pentru aer, impedanța acustică specifică z este 420 kg.s-1.m-2 = 420 Pa.s.m-1. Pentru apă (dulce), impedanța acustică specifică pentru apă este de 1,48 MPa.s.m-1. Așadar, o undă sonoră în apă cu aceeași presiune are o intensitate mult mai mică decât una în aer.

dBi și radiația care variază în funcție de direcție

Radiația care variază în funcție de direcție se numește anizotropă. Pentru multe cazuri în comunicații, radiația izotropă este risipitoare: de ce să emiți o fracțiune substanțială de putere în sus dacă receptorul este, ca și tine, relativ aproape de nivelul solului. Pentru sunetele cu lungime de undă scurtă (inclusiv cea mai mare parte a intervalului important pentru vorbire), un megafon poate contribui la creșterea anizotropiei vocii. Pentru radio, o gamă largă de modele permite antenelor să fie foarte anizotrope atât pentru emisie, cât și pentru recepție.

Atunci, atunci când vă interesează emisia într-o anumită direcție (sau recepția dintr-o anumită direcție), doriți ca raportul dintre intensitatea măsurată în acea direcție, la o anumită distanță, să fie mai mare decât cea măsurată la aceeași distanță de la un radiator izotrop (sau recepționată de un receptor izotrop). Acest raport se numește câștig; exprimați raportul în dB și veți obține câștigul în dBi pentru radiatorul respectiv. Această unitate este utilizată în principal pentru antene, fie de emisie, fie de recepție, dar uneori este utilizată pentru surse de sunet și microfoane direcționale.

Exemple de probleme

Câteva persoane au scris cerând exemple de utilizare a dB în calcule. Așadar…
• În condiții de egalitate, cu cât este mai tare un difuzor acționat (în gama sa liniară) de un amplificator de 100 W decât de un amplificator de 10 W?

  Puterile diferă cu un factor de zece, care, așa cum am văzut mai sus, este de 10 dB. Toate celelalte elemente egale înseamnă aici că răspunsurile în frecvență sunt egale și că se utilizează același semnal de intrare etc. Așadar, dependența de frecvență ar trebui să fie aceeași. 10 dB corespunde la 10 phoni. Pentru a obține o dublare percepută a intensității sonore, aveți nevoie de o creștere de 10 phons. Așadar, difuzorul acționat de un amplificator de 100 W este de două ori mai puternic decât atunci când este acționat de un amplificator de 10 W, presupunând că rămâneți în intervalul liniar și că nu distorsionați sau distrugeți difuzorul. (Amplificatorul de 100 W produce de două ori mai mulți foni decât cel de 10 W.)

• Eu mă aflu la o distanță R de o sursă mică de sunet (dimensiune mult mai mică decât R), la nivelul solului, în aer liber, unde reflexiile pot fi neglijate. Nivelul sunetului este L. Dacă mă deplasez acum la o distanță nR (n este un număr, iar nR este încă mult mai mare decât dimensiunea sursei), care va fi noul nivel al sunetului?

  În primul rând, rețineți că neglijarea reflexiilor este foarte importantă. Acest calcul nu va funcționa în interiorul unei încăperi, unde reflexiile de pe pereți (care produc colectiv reverberația) fac calculul destul de dificil. În aer liber, intensitatea sunetului este proporțională cu 1/r2, unde r este distanța de la sursă. (Constanta de proporționalitate depinde de cât de bine reflectă solul și nu ne interesează aici, deoarece se va anula aproximativ în calcul, cu condiția ca r să fie rezonabil de mare). Așadar, dacă mărim r de la R la nR, diminuăm intensitatea de la I la I/n 2.

  Diferența în decibeli dintre cele două semnale de intensitate I 2 și I 1 este definită mai sus ca fiind

  ΔL = 10 log (I2/I1) = 10 log ((I/n 2)/I) = 10 log (1/n 2) = -10 log (n 2) = -20 log n.

  De exemplu, dacă n este 2 (adică dacă mergem de două ori mai departe), intensitatea se reduce de patru ori, iar nivelul sonor scade de la L la (L – 6dB).

• Dacă, în condiții ideale de liniște, o persoană tânără poate auzi un ton de 1 kHz la 0 dB emis de un difuzor (poate un softspeaker?), cu cât trebuie crescută puterea difuzorului pentru a ridica sunetul la 110 dB (un nivel periculos de puternic, dar care permite supraviețuirea)?

  Diferența în decibeli dintre cele două semnale de putere P2 și P1 este definită mai sus ca fiind

  ΔL = 10 log (P2/P1) dB deci, ridicând cu 10 la puterea acestor două mărimi egale:
  10L/10 = P2/P1 deci:
  P2/P1 = 10110/10 = 1011 = o sută de mii de milioane.

  care este o demonstrație că urechea umană are o gamă dinamică remarcabil de mare, poate mai mare decât cea a ochiului.

• Un amplificator are o intrare de 10 mV și o ieșire de 2 V. Care este câștigul său de tensiune în dB?

  Tensiunea, ca și presiunea, apare la pătrat în expresiile pentru putere sau intensitate. (Puterea disipată într-un rezistor R este V2/R.) Deci, prin convenție, definim:

  gain = 20 log (Vout/Vin)
  = 20 log (2V/10mV)
  = 46 dB

  (În cazurile acustice prezentate mai sus, am văzut că raportul de presiune, exprimat în dB, a fost același cu raportul de putere: acesta a fost motivul pentru factorul 20 atunci când se definește dB pentru presiune. Este demn de remarcat faptul că, în exemplul câștigului de tensiune, este puțin probabil ca câștigul de putere al amplificatorului să fie egal cu câștigul de tensiune, care este definit prin convenția utilizată aici. Puterea este proporțională cu pătratul tensiunii într-un anumit rezistor. Cu toate acestea, impedanțele de intrare și de ieșire ale amplificatoarelor sunt adesea destul de diferite. De exemplu, un amplificator tampon sau un follower de emitor are un câștig de tensiune de aproximativ 1, dar un câștig de curent mare).

• Care este diferența, în dB, între iradierea (intensitatea luminii) pe Pământ (8,3 minute lumină de la Soare) și pe Uranus (160 de minute lumină)?

  Ca și sunetul, intensitatea izotropă a luminii scade ca r-2, deci raportul de intensitate este (160/8.3)2 = 20 log (160/8,3) = 26 dB.

Sănătate și securitate în muncă

Diferitele țări și provincii au, evident, legi diferite privind expunerea la zgomot la locul de muncă, care sunt aplicate cu entuziasm diferit. Multe dintre aceste reglementări au o limită de expunere la zgomot continuu de 85 dB(A), pentru un schimb de 8 ore. Pentru fiecare creștere de 3 dB, expunerea permisă se reduce la jumătate. Astfel, dacă lucrați într-un club de noapte unde muzica amplificată produce 100 dB(A) în apropierea urechilor dumneavoastră, expunerea permisă este de 15 minute. Există o limită pentru zgomotul de impuls, cum ar fi armele de foc sau uneltele care folosesc lovituri explozive. (de exemplu, 140 dB de vârf nu ar trebui să fie depășit în niciun moment al zilei.) Există numeroase documente care oferă sfaturi despre cum să reduceți expunerea la zgomot la sursă (de exemplu, reduceți nivelul muzicii), între sursă și ureche (de exemplu, îndepărtați-vă de difuzoare la un concert) și la nivelul urechii (de exemplu, purtați dopuri pentru urechi sau protecții auditive industriale). Gestionarea zgomotului și protecția auzului la locul de muncă este codul de practică în statul New South Wales, Australia (adresa autorului).

Câteva întrebări frecvente

• Cât de tare este un avion? Un tren? O persoană care cântă? Un câine care latră? O unealtă electrică? Răspunsurile la această întrebare variază considerabil. Depinde foarte mult de distanța la care vă aflați, dacă sunteți în interior sau nu, dacă există reverberație, cât de puternică este sursa respectivă și care este spectrul acesteia. Oferirea unor valori, fără a fi foarte precisă în ceea ce privește condițiile, ar fi oarecum înșelătoare. Deoarece restul acestei pagini se dorește a fi fiabilă, atât cât este posibil, aș prefera să nu dau valori aici.
• Cum se „adaugă decibeli”, adică Ce nivel de sunet obțineți când adăugați nivelul a la nivelul b? Dacă sursele sunt coerente (ceea ce înseamnă, de obicei, că în cele din urmă provin din aceeași sursă), atunci pot exista efecte de interferență complicate. În majoritatea cazurilor, în care sursele sunt independente, se pot adăuga intensitățile și apoi se pot converti în decibeli. Cu toate acestea, dacă vi se dau nivelurile sonore în dB(A), nu este atât de ușor să vă întoarceți la intensitate și trebuie să știți ceva despre spectrul sunetului. Dacă cunoașteți distribuția sunetului în diferite benzi de frecvență, puteți utiliza applet-ul de pe acest link.
• Some of the questions on our FAQ in music acoustics relate to decibels, including
  • Why do the sounds of two musical instruments always reinforce, and never cancel out?
  • How much does one more violin add to the sound level of a section of n violins?
  • Does adding two equal sounds give an increase of 3 or 6 dB? Why?
  • What is the loudest sound?
  • Is there really no sound in space?

Related pages

• Measure your own hearing response
• Adding sound levels from incoherent sources
• What are interference beats and Tartini tones?
• FAQ in music acoustics
• Loudness and spectra: how spectral content and other features are related to loudness
• Formants: what are they? A discussion of the different meanings of this term
• Music acoustics home page
• Physclips: a multi-level, multimedia introduction to mechanics.
• A list of other educational web sites from this author.