Distribuția Marginală
Distribuții de probabilitate > Distribuția Marginală
Ce este o distribuție Marginală?
Vizionați videoclipul sau citiți articolul de mai jos:
Definiția tehnică poate fi puțin amețitoare la care să te uiți:
Definiția unei distribuții marginale = Dacă X și Y sunt variabile aleatoare discrete și f (x,y) este valoarea
distribuției lor comune de probabilitate la (x,y), funcțiile date de:
g(x) = Σy f (x,y) și h(y) = Σx f (x,y) sunt distribuțiile marginale ale lui X și Y , respectiv.
Dacă vă descurcați de minune cu ecuațiile, probabil că asta este tot ce trebuie să știți. Vă spune cum să găsiți o distribuție marginală. Dar dacă această formulă vă dă bătăi de cap (ceea ce se întâmplă cu majoritatea oamenilor!), puteți folosi un tabel de distribuție a frecvențelor pentru a găsi o distribuție marginală.
O distribuție marginală își primește numele deoarece apare în marginile unui tabel de distribuție a probabilităților.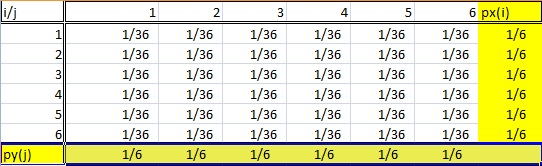
Desigur, nu este chiar atât de simplu ca asta. Nu puteți să vă uitați la orice tabel vechi de distribuție a frecvențelor și să spuneți că ultima coloană (sau ultimul rând) este o „distribuție marginală”. Distribuțiile marginale respectă câteva reguli:
- Distribuția trebuie să fie din date bivariate. Bivariată este doar un alt mod de a spune „două variabile”, cum ar fi X și Y. În tabelul de mai sus, variabilele aleatoare i și j provin din aruncarea a două zaruri.
- O distribuție marginală este cea în care sunteți interesat doar de una dintre variabilele aleatoare . Cu alte cuvinte, fie X, fie Y. Dacă vă uitați la tabelul de probabilități de mai sus, probabilitățile de sumă ale unei variabile sunt enumerate în rândul de jos, iar celelalte probabilități de sumă sunt enumerate în coloana din dreapta. Deci, acest tabel are două distribuții marginale.
Diferența dintre distribuția marginală și distribuția condiționată.
O distribuție condiționată este cea în care suntem interesați doar de o anumită subpopulație din întregul nostru set de date. În exemplul cu aruncarea zarurilor, aceasta ar putea fi „aruncarea unui doi” sau „aruncarea unui șase”. Imaginea de mai jos arată două subpopulații evidențiate (și, prin urmare, două distribuții condiționate).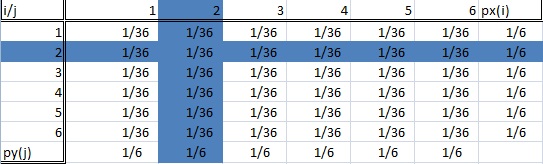
Cum se calculează distribuția marginală a probabilității
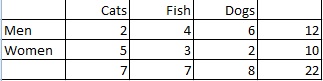
Întrebare de exemplu: Calculați distribuția marginală a preferinței pentru animale de companie între bărbați și femei:
Soluție:
Pasul 1: Numărați numărul total de persoane. În acest caz, totalul este dat în coloana din dreapta (22 de persoane).
Pasul 2: Numărați numărul de persoane care preferă fiecare tip de animal de companie și apoi transformați raportul într-o probabilitate:
Persoane care preferă pisicile: 7/22 = 0,32
Persoane care preferă peștii: 7/22 = 0,32
Persoane care preferă câinii: 8/22 = 0,36
Tip: Vă puteți verifica răspunsul asigurându-vă că toate probabilitățile însumează 1.
Întrebare de exemplu 2 (Evenimente care se exclud reciproc): Dacă P(A) = 0,20, P(b) = 0,70, iar ambele evenimente se exclud reciproc, găsiți P(B’∩A), P(B’∩A’) și P(B∩A’).
Dacă nu sunteți familiarizați cu această notație, P(A’) înseamnă „nu A”, sau complementul. P(B’∩A) înseamnă „intersecția dintre nu B și A”).
Răspuns:
Ați putea calcula probabilitățile individual, dar acestea sunt mult mai ușor de calculat folosind un tabel.
Pasul 1: Completați un tabel de frecvențe cu informațiile date. Probabilitatea totală trebuie să fie egală cu 1, așa că o puteți adăuga și pe aceasta la marje(totaluri). O simplă adunare/algebră completează spațiile libere marginale. De exemplu, pe rândul de jos 0,70 + x = 1,00, astfel încât Totalul marginal pentru B’ trebuie să fie 0,30.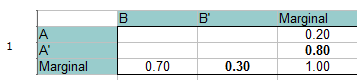
Pasul 2: Adăugați 0 pentru intersecția dintre A și B, în stânga sus a tabelului. Puteți face acest lucru deoarece A și B se exclud reciproc și nu se pot întâmpla împreună.
Pasul 3: Completați restul spațiilor libere folosind adunarea/algebra simplă.
Lecturați din tabel (uitați-vă la intersecțiile celor două probabilități enunțate):
P(B’∩A) = 0,20
P(B’∩A’) = 0,10
P(B∩A’) = 0,70.
Întrebare de exemplu 3 (Evenimente independente): Dacă P(A) = 0,20, P(b) = 0,70 și ambele evenimente sunt independente, găsiți P(B’∩A), P(B’∩A’) și P(B∩A’).
Răspuns: P(B’∩A’): De data aceasta, A și B sunt independente, deci probabilitatea ca ambele să se întâmple în același timp este 0,14 (P(A)*P(B) = 0,20 * 0,70 = 0,14). Această valoare se plasează în stânga sus (intersecția dintre A și B). Completați restul tabelului exact la fel ca în pașii de mai sus.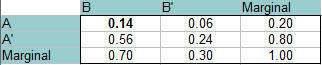
Căutați răspunsurile din tabel (de la intersecțiile celor două probabilități):
P(B’∩A): 0.06
P(B’∩A’): 0,24
P(B∩A’): 0,56.
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. (Tabele matematice standard). Boca Raton, FL: CRC Press, pp. 536 și 571, 2002.
Agresti A. (1990) Analiza datelor categoriale. John Wiley and Sons, New York.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
Stephanie Glen. „Marginal Distribution” de pe StatisticsHowTo.com: Statistică elementară pentru noi toți ceilalți! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/marginal-distribution/
——————————————————————————
Nevoie de ajutor cu o temă pentru acasă sau o întrebare de test? Cu Chegg Study, puteți obține soluții pas cu pas la întrebările dvs. de la un expert în domeniu. Primele 30 de minute cu un tutore Chegg sunt gratuite!