Tipuri de interpolare – Avantaje și dezavantaje
Metode de interpolare
Interpolarea este procesul de utilizare a punctelor cu valori cunoscute sau a punctelor de eșantionare pentru a estima valori în alte puncte necunoscute. Poate fi utilizată pentru a prezice valori necunoscute pentru orice date punctuale geografice, cum ar fi altitudinea, precipitațiile, concentrațiile chimice, nivelurile de zgomot și așa mai departe.
Metodele de interpolare disponibile sunt enumerate mai jos.
Interpolator cu ponderare inversă a distanței (IDW)
Inverse Distance Weighted (IDW)
Interpolatorul cu ponderare inversă a distanței presupune că fiecare punct de intrare are o influență locală care se diminuează odată cu distanța. Acesta ponderează punctele mai apropiate de celula de procesare mai mult decât cele mai îndepărtate. Un număr specificat de puncte sau toate punctele de pe o rază specificată pot fi utilizate pentru a determina valoarea de ieșire a fiecărei locații. Utilizarea acestei metode presupune că variabila care este cartografiată scade în influență cu distanța de la locația sa eșantionată.
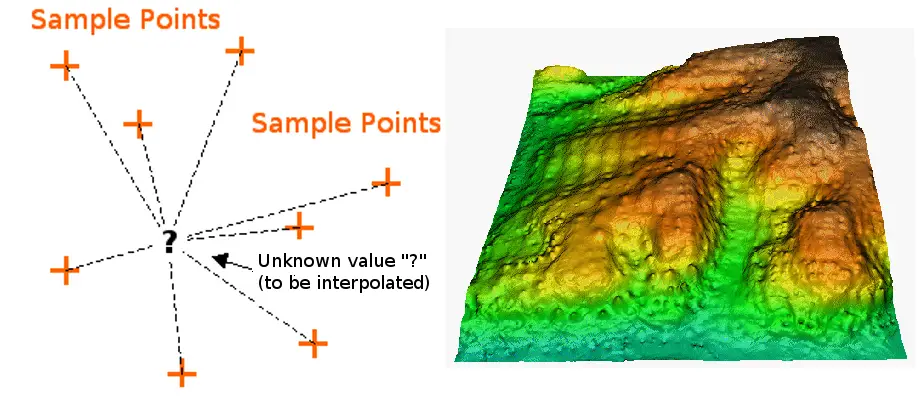
IDW Interpolation; Prin amabilitatea: ESRI: QGIS
Algoritmul de ponderare inversă a distanței (IDW) este efectiv un interpolator de medie mobilă care se aplică de obicei la date foarte variabile. Pentru anumite tipuri de date este posibil să se revină la locul de colectare și să se înregistreze o nouă valoare care este diferită din punct de vedere statistic de citirea inițială, dar care se încadrează în tendința generală pentru zona respectivă.
Suprafața interpolată, estimată cu ajutorul unei tehnici de medie mobilă, este mai mică decât valoarea maximă locală și mai mare decât valoarea minimă locală.

Suprafață interpolatăIDW; Courtesy:ESRI
InterpolareaIDW implementează în mod explicit ipoteza conform căreia lucrurile care sunt apropiate unele de altele sunt mai asemănătoare decât cele care sunt mai îndepărtate. Pentru a prezice o valoare pentru orice locație nemăsurată, IDW va utiliza valorile măsurate din jurul locației de predicție. Valorile măsurate cele mai apropiate de locația de predicție vor avea o influență mai mare asupra valorii prezise decât cele mai îndepărtate. Astfel, IDW presupune că fiecare punct măsurat are o influență locală care se diminuează odată cu distanța. Funcția IDW ar trebui să fie utilizată atunci când setul de puncte este suficient de dens pentru a capta amploarea variației locale a suprafeței necesare pentru analiză. IDW determină valorile celulelor utilizând un set de puncte de eșantionare combinate cu ponderare liniară. Aceasta ponderează punctele mai apropiate de locația de predicție mai mult decât cele mai îndepărtate, de unde și denumirea de ponderare inversă a distanței.
Tehnica IDW calculează o valoare pentru fiecare nod de grilă prin examinarea punctelor de date înconjurătoare care se află în interiorul unei raze de căutare definite de utilizator. O parte sau toate punctele de date pot fi utilizate în procesul de interpolare. Valoarea nodului este calculată prin medierea sumei ponderate a tuturor punctelor. Punctele de date care se află progresiv mai departe de nod influențează valoarea calculată mult mai puțin decât cele care se află mai aproape de nod.
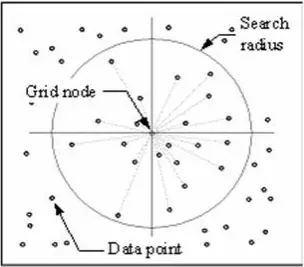
În jurul fiecărui nod de grilă se generează o rază din care se selectează punctele de date pentru a fi utilizate în calcul. Options to control the use of IDW include power, search radius, fixed search radius, variable search radius and barrier.
Note: The optimal power (p) value is determined by minimizing the root mean square prediction error (RMSPE).
Advantages
- Can estimate extreme changes in terrain such as: Cliffs, Fault Lines.
- Dense evenly space points are well interpolated (flat areas with cliffs).
- Can increase or decrease amount of sample points to influence cell values.
Disadvantages
- Cannot estimate above maximum or below minimum values.
- Not very good for peaks or mountainous areas.
Natural Neighbour Inverse Distance Weighted (NNIDW)
Natural neighbor interpolation has many positive features, can be used for both interpolation and extrapolation, and generally works well with clustered scatter points. O altă metodă a mediei ponderate, ecuația de bază utilizată în interpolarea cu vecini naturali este identică cu cea utilizată în interpolarea IDW. Această metodă poate gestiona în mod eficient seturi mari de date de puncte de intrare. Atunci când se utilizează metoda Natural Neighbor, coordonatele locale definesc gradul de influență pe care orice punct de dispersie îl va avea asupra celulelor de ieșire.
Metoda Natural Neighbor este o tehnică de estimare geometrică care utilizează regiuni de vecinătate naturală generate în jurul fiecărui punct din setul de date.
Ca și IDW, această metodă de interpolare este o metodă de interpolare cu medie ponderată. Cu toate acestea, în loc să găsească valoarea unui punct interpolat folosind toate punctele de intrare ponderate în funcție de distanța lor, interpolarea Natural Neighbors creează o triangulație Delauney a punctelor de intrare și selectează cele mai apropiate noduri care formează o coajă convexă în jurul punctului de interpolare, apoi le ponderează valorile în funcție de aria proporțională. Această metodă este cea mai potrivită în cazul în care punctele de eșantionare a datelor sunt distribuite cu o densitate neuniformă. Este o bună tehnică de interpolare de uz general și are avantajul că nu trebuie să specificați parametri precum raza, numărul de vecini sau ponderile.

Natural IDW: Courtesy: ESRI
Această tehnică este concepută pentru a onora valorile minime și maxime locale din fișierul de puncte și poate fi setată pentru a limita depășirile valorilor ridicate locale și depășirile valorilor scăzute locale. Metoda permite astfel crearea de modele de suprafață precise din seturi de date care sunt foarte slab distribuite sau foarte liniare în distribuția spațială.
Vantaje
- Manipulează eficient un număr mare de puncte de eșantionare.
Spline
Spline estimează valorile folosind o funcție matematică care minimizează curbura generală a suprafeței, rezultând o suprafață netedă care trece exact prin punctele de intrare.

Spline: Courtesy: ESRI
Conceptual, este analog cu îndoirea unei foi de cauciuc pentru a trece prin puncte cunoscute, minimizând în același timp curbura totală a suprafeței. Se adaptează o funcție matematică la un număr specificat de puncte de intrare cele mai apropiate, trecând în același timp prin punctele de eșantionare. Această metodă este cea mai bună pentru suprafețe care variază ușor, cum ar fi altitudinea, înălțimea pânzei freatice sau concentrațiile de poluare.
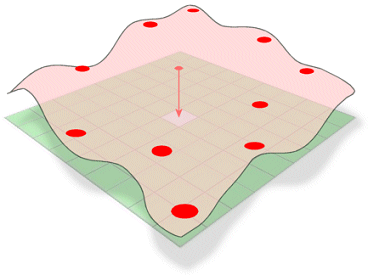
Metoda Spline de interpolare estimează valori necunoscute prin curbarea unei suprafețe prin valori cunoscute.
Există două metode spline: regularizată și de tensiune.
O metodă regularizată creează o suprafață netedă, care se schimbă treptat, cu valori care se pot afla în afara intervalului de date din eșantion. Aceasta încorporează prima derivată (panta), a doua derivată (rata de variație a pantei) și a treia derivată (rata de variație a celei de-a doua derivate) în calculele sale de minimizare.
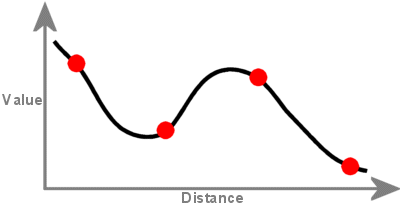
O suprafață creată cu interpolare Spline trece prin fiecare punct de eșantionare și poate depăși intervalul de valori al setului de puncte de eșantionare.
Deși o spline Tension utilizează doar prima și a doua derivată, aceasta include mai multe puncte în calculele Spline, ceea ce creează de obicei suprafețe mai netede, dar crește timpul de calcul.
Această metodă trage o suprafață peste punctele achiziționate, rezultând un efect de întindere. Spline utilizează linii curbe (metoda Liniilor curbilinii) pentru a calcula valorile celulelor.
Scoaterea unei ponderi pentru interpolările Spline
Spline regularizat: Cu cât ponderea este mai mare, cu atât suprafața este mai netedă. Greutățile între 0 și 5 sunt potrivite. Valorile tipice sunt 0, 0,001, 0,01, 0,1 și 0,5.
Tension spline: Cu cât ponderea este mai mare, cu atât suprafața este mai grosieră și valorile sunt mai conforme cu intervalul de date al eșantionului. Valorile ponderale trebuie să fie mai mari sau egale cu zero. Typical values are 0, 1, 5, and 10.
Advantages
- Useful for estimating above maximum and below minimum points.
- Creates a smooth surface effect.
Disadvantages
- Cliffs and fault lines are not well presented because of the smoothing effect.
- When the sample points are close together and have extreme differences in value, Spline interpolation doesn’t work as well. This is because Spline uses slope calculations (change over distance) to figure out the shape of the flexible rubber sheet.
Kriging
Kriging is a geostatistical interpolation technique that considers both the distance and the degree of variation between known data points when estimating values in unknown areas. A kriged estimate is a weighted linear combination of the known sample values around the point to be estimated.
Procedură de kriging care generează o suprafață estimată dintr-un set împrăștiat de puncte cu valori z. Kriging presupune că distanța sau direcția dintre punctele de eșantionare reflectă o corelație spațială care poate fi utilizată pentru a explica variația din suprafață. Instrumentul Kriging ajustează o funcție matematică la un număr specificat de puncte sau la toate punctele aflate pe o rază specificată, pentru a determina valoarea de ieșire pentru fiecare locație. Kriging este un proces în mai multe etape; acesta include analiza statistică exploratorie a datelor, modelarea variogramei, crearea suprafeței și (opțional) explorarea unei suprafețe de variație. Kriging este cel mai potrivit atunci când știți că există o distanță corelată spațial sau o distorsiune direcțională în date. Este adesea utilizat în știința solului și în geologie.
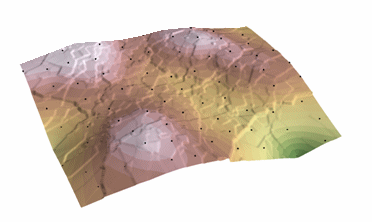
Kriging: Courtesy: ESRI
The predicted values are derived from the measure of relationship in samples using sophisticated weighted average technique. It uses a search radius that can be fixed or variable. The generated cell values can exceed value range of samples, and the surface does not pass through samples.
The Kriging Formula
Kriging is similar to IDW in that it weights the surrounding measured values to derive a prediction for an unmeasured location. The general formula for both interpolators is formed as a weighted sum of the data:
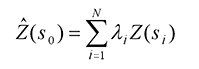
- where:
Z(si) = the measured value at the ith location
λi = an unknown weight for the measured value at the ith location
s0 = the prediction location
N = the number of measured values
In IDW, the weight, λi, depends solely on the distance to the prediction location. Cu toate acestea, în cazul metodei kriging, ponderile se bazează nu numai pe distanța dintre punctele măsurate și locația de predicție, ci și pe dispunerea spațială globală a punctelor măsurate. Pentru a utiliza aranjamentul spațial în ponderi, trebuie cuantificată autocorelația spațială. Astfel, în krigingul obișnuit, ponderea, λi, depinde de un model adaptat la punctele măsurate, de distanța până la locul de predicție și de relațiile spațiale dintre valorile măsurate în jurul locului de predicție. Următoarele secțiuni analizează modul în care formula generală de kriging este utilizată pentru a crea o hartă a suprafeței de predicție și o hartă a preciziei predicțiilor.
Tipuri de Kriging
Kriging ordinar
Krigingul ordinar presupune modelul
Z(s) = µ + ε(s),
unde µ este o constantă necunoscută. Una dintre principalele probleme referitoare la krigingul obișnuit este dacă ipoteza unei medii constante este rezonabilă. Sometimes there are good scientific reasons to reject this assumption. However, as a simple prediction method, it has remarkable flexibility.
Ordinary kriging can use either semivariograms or covariances, use transformations and remove trends, and allow for measurement error.
Simple Kriging
Simple kriging assumes the model
Z(s) = µ + ε(s),
where µ is a known constant.
Simple kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Universal Kriging
Universal kriging assumes the model
Z(s) = µ(s) + ε(s),
where µ(s) is some deterministic function.
Universal kriging can use either semivariograms or covariances, use transformations, and allow for measurement error.
Indicator Kriging
Indicator kriging presupune modelul
I(s) = µ + ε(s),
unde µ este o constantă necunoscută și I(s) este o variabilă binară. Crearea datelor binare se poate face prin utilizarea unui prag pentru datele continue sau se poate întâmpla ca datele observate să fie 0 sau 1. De exemplu, este posibil să aveți un eșantion care constă în informații despre faptul dacă un punct este sau nu un habitat forestier sau neforestier, unde variabila binară indică apartenența la o clasă. Utilizând variabile binare, krigingul indicator procedează la fel ca și krigingul obișnuit.
Krigingul indicator poate utiliza fie semivariograme, fie covarianțe.
Probability Kriging
Probability kriging presupune modelul
I(s) = I(Z(s) > ct) = µ1 + ε1(s)Z(s) = µ2 + ε2(s),
unde µ1 și µ2 sunt constante necunoscute, iar I(s) este o variabilă binară creată prin utilizarea unui indicator de prag, I(Z(s) > ct). Observați că acum există două tipuri de erori aleatoare, ε1(s) și ε2(s), astfel încât există autocorelație pentru fiecare dintre ele și corelație încrucișată între ele. Probability kriging se străduiește să facă același lucru ca și indicator kriging, dar utilizează cokriging în încercarea de a face o treabă mai bună.
Krigingul probabilistic poate utiliza fie semivariograme, fie covarianțe, covarianțe încrucișate și transformări, dar nu poate permite erori de măsurare.
style=”display:inline-block;width:468px;height:60px” data-ad-client=”ca-pub-7134201556760050″ data-ad-slot=”9271753327″>
Kriging disjunctiv
Krigingul disjunctiv pornește de la ipoteza că model
f(Z(s)) = µ1 + ε(s),
unde µ1 este o constantă necunoscută și f(Z(s)) este o funcție arbitrară a lui Z(s). Observați că se poate scrie f(Z(s)) = I(Z(s) > ct), deci krigingul indicator este un caz special de kriging disjunctiv. În Geostatistical Analyst, puteți prezice fie valoarea în sine, fie un indicator cu kriging disjunctiv.
În general, krigingul disjunctiv încearcă să facă mai mult decât krigingul obișnuit. Deși recompensele pot fi mai mari, la fel sunt și costurile. Disjunctive kriging requires the bivariate normality assumption and approximations to the functions fi(Z(si)); the assumptions are difficult to verify, and the solutions are mathematically and computationally complicated.
Disjunctive kriging can use either semivariograms or covariances and transformations, but it cannot allow for measurement error.
Advantages
- Directional influences can be accounted for: Soil Erosion, Siltation Flow, Lava Flow and Winds.
- Exceeds the minimum and maximum point values
Disadvantages
- Does not pass through any of the point values and causes interpolated values to be higher or lower then real values.
** Pentru a avea o perspectivă profundă asupra abordării matematice privind Kriging, vă rugăm să faceți clic pe Kriging a Interpolation Method.
PointInterp
O metodă care este similară cu IDW, funcția PointInterp permite un control mai mare asupra vecinătății de eșantionare. Influența unui anumit eșantion asupra valorii celulei de grilă interpolate depinde de faptul dacă punctul de eșantionare se află în vecinătatea celulei și de distanța la care se află față de celula care se interpolează. Punctele din afara vecinătății nu au nicio influență.

PointInterp; Courtesy: ESRI
Valoarea ponderată a punctelor din interiorul vecinătății este calculată utilizând o interpolare ponderată cu distanța inversă sau o interpolare exponențială inversă a distanței. Această metodă interpolează un raster folosind caracteristici punctuale, dar permite diferite tipuri de vecinătăți. Vecinătățile pot avea forme cum ar fi cercuri, dreptunghiuri, poligoane neregulate, anule sau pene.
Trend
Trendul este o metodă statistică care găsește suprafața care se potrivește punctelor din eșantion folosind o potrivire prin regresie cu cel mai mic pătrat. Aceasta ajustează o ecuație polinomială la întreaga suprafață. Astfel se obține o suprafață care minimizează variația suprafeței în raport cu valorile de intrare. Suprafața este construită astfel încât, pentru fiecare punct de intrare, totalul diferențelor dintre valorile reale și valorile estimate (adică varianța) să fie cât mai mic posibil.

Trend; Courtsey:ESRI
Este un interpolator inexact, iar suprafața rezultată trece rareori prin punctele de intrare. Cu toate acestea, această metodă detectează tendințele în datele eșantionate și este similară cu fenomenele naturale care variază de obicei lin.
Avantaje
- Suprafețele de tendință sunt bune pentru identificarea modelelor la scară grosieră în date; suprafața interpolată trece rareori prin punctele de eșantionare.
Topo to Raster
Prin interpolarea valorilor de elevație pentru un raster, metoda Topo to Raster impune constrângeri care asigură un model digital de elevație corect din punct de vedere hidrologic, care conține o structură de drenaj conectată și reprezintă corect crestele și cursurile de apă din datele de contur de intrare. Metoda utilizează o tehnică de interpolare iterativă cu diferențe finite care optimizează eficiența computațională a interpolării locale fără a pierde continuitatea suprafeței în cazul interpolării globale. A fost conceput special pentru a funcționa în mod inteligent cu intrările de contur.
Mai jos este un exemplu de suprafață interpolată din puncte de elevație, curbe de nivel, linii de curgere și poligoane de lac folosind interpolarea Topo to Raster.
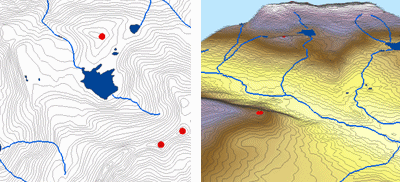
Topo to raster; Courtesy: ESRI
Topo to Raster este un instrument specializat pentru crearea de suprafețe raster corecte din punct de vedere hidrologic din datele vectoriale ale componentelor terenului, cum ar fi punctele de elevație, curbele de nivel, liniile de curgere, poligoanele lacurilor, punctele de scufundare și poligoanele de delimitare a zonei de studiu.
Densitate
Uneltele de densitate (disponibile în ArcGIS) produc o suprafață care reprezintă cât de mult sau cât de multe dintr-un anumit lucru există pe unitatea de suprafață. Instrumentul de densitate este util pentru a crea suprafețe de densitate pentru a reprezenta distribuția unei populații de animale sălbatice pornind de la un set de observații sau gradul de urbanizare a unei zone pe baza densității drumurilor.

Density Raster; Courtest: ERSI
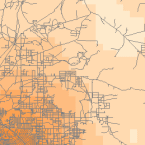
Density and Roads; Courtesy: ESRI
There are density tools for point and line features in ArcGIS.
Related Topics
- What is Interpolation ?
- Classification of Interpolation Techniques.
- Choosing the Right Interpolation Method