Vlnová délka

V lineárním prostředí lze jakýkoli vlnový průběh popsat jako nezávislé šíření sinusových složek. Vlnová délka λ sinusového vlnění šířícího se konstantní rychlostí v je dána vztahem

λ = v f , {\displaystyle \lambda ={\frac {v}{f}},\,,}

kde v se nazývá fázová rychlost (velikost fázové rychlosti) vlny a f je frekvence vlny. V disperzním prostředí závisí samotná fázová rychlost na frekvenci vlny, takže vztah mezi vlnovou délkou a frekvencí je nelineární.

V případě elektromagnetického záření – jako je světlo – ve volném prostoru je fázová rychlost rovna rychlosti světla, tedy přibližně 3×108 m/s. Vlnová délka elektromagnetické (rádiové) vlny o frekvenci 100 MHz je tedy přibližně: 3×108 m/s děleno 108 Hz = 3 metry. Vlnová délka viditelného světla se pohybuje od tmavě červené, zhruba 700 nm, po fialovou, zhruba 400 nm (další příklady viz elektromagnetické spektrum).

Pro zvukové vlny ve vzduchu platí, že rychlost zvuku je 343 m/s (při pokojové teplotě a atmosférickém tlaku). Vlnové délky zvukových frekvencí slyšitelných lidským uchem (20 Hz-20 kHz) se tedy pohybují přibližně mezi 17 m a 17 mm. Netopýři používají poněkud vyšší frekvence, aby mohli rozlišit cíle menší než 17 mm. Vlnové délky slyšitelného zvuku jsou mnohem delší než vlnové délky viditelného světla.

Sinusové stojaté vlny v krabici, která omezuje koncové body na uzly, budou mít celočíselný počet půlvln, které se do krabice vejdou.

A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue)

Standing wavesEdit

A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.

The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Například pro elektromagnetickou vlnu, má-li krabice ideální kovové stěny, vyplývá podmínka uzlů u stěn z toho, že kovové stěny nemohou udržet tečné elektrické pole, což nutí vlnu mít u stěny nulovou amplitudu.

Na stojatou vlnu lze pohlížet jako na součet dvou putujících sinusových vln s opačně směrovanými rychlostmi. Z toho vyplývá, že vlnová délka, perioda a rychlost vlny spolu souvisejí stejně jako u vlny putující. Například rychlost světla lze určit z pozorování stojatých vln v kovové skříňce obsahující ideální vakuum.

Matematické znázorněníUpravit

Putující sinusové vlny se často matematicky znázorňují pomocí jejich rychlosti v (ve směru x), frekvence f a vlnové délky λ jako:

y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ ( x – v t ) ). {\displaystyle y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}

kde y je hodnota vlny v libovolné poloze x a čase t a A je amplituda vlny. Běžně se také vyjadřují pomocí vlnového čísla k (2π násobek reciproké vlnové délky) a úhlové frekvence ω (2π násobek frekvence) takto:

y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}

v němž vlnová délka a vlnové číslo souvisí s rychlostí a frekvencí jako:

k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},}

nebo

λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.}

V druhém výše uvedeném tvaru se fáze (kx – ωt) často zobecňuje na (k-r – ωt), a to tak, že se vlnové číslo k nahradí vlnovým vektorem, který udává směr a vlnové číslo rovinné vlny v 3-prostoru, parametrizované polohovým vektorem r. V takovém případě je vlnové číslo k, tedy velikost k, stále ve stejném vztahu k vlnové délce, jak je uvedeno výše, přičemž v je interpretováno jako skalární rychlost ve směru vlnového vektoru. První tvar, využívající reciproční vlnovou délku ve fázi, se nedá tak snadno zobecnit na vlnu v libovolném směru.

Běžná jsou také zobecnění na sinusoidy jiných fází a na komplexní exponenciály; viz rovinná vlna. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave

A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit

Wavelength is decreased in a medium with slower propagation.

Refraction: upon entering a medium where its speed is lower, the wave changes direction.

Separation of colors by a prism (click for animation)

The speed of a wave depends upon the medium in which it propagates. Konkrétně je rychlost světla v prostředí menší než ve vakuu, což znamená, že stejné frekvenci bude v prostředí odpovídat kratší vlnová délka než ve vakuu, jak je znázorněno na obrázku vpravo.

Tato změna rychlosti při vstupu do prostředí způsobuje refrakci neboli změnu směru vlnění, které narazí na rozhraní mezi prostředími pod úhlem. U elektromagnetických vln se tato změna úhlu šíření řídí Snellovým zákonem.

Rychlost vlnění v jednom prostředí se nejen může lišit od rychlosti v jiném prostředí, ale rychlost se obvykle mění s vlnovou délkou. V důsledku toho se změna směru při vstupu do jiného prostředí mění s vlnovou délkou vlny.

U elektromagnetických vln se rychlost v prostředí řídí jeho indexem lomu podle

v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},} }

kde c je rychlost světla ve vakuu a n(λ0) je index lomu prostředí při vlnové délce λ0, přičemž tento index se měří spíše ve vakuu než v prostředí. Odpovídající vlnová délka v prostředí je

λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}.

Při uvádění vlnových délek elektromagnetického záření se obvykle myslí vlnová délka ve vakuu, pokud není vlnová délka výslovně označena jako vlnová délka v jiném prostředí. V akustice, kde je prostředí pro existenci vlnění nezbytné, se hodnota vlnové délky udává pro určité prostředí.

Změna rychlosti světla s vlnovou délkou je známá jako disperze a je také zodpovědná za známý jev, kdy se světlo pomocí hranolu rozdělí na jednotlivé složky barvy. K rozdělení dochází, když se index lomu uvnitř hranolu mění s vlnovou délkou, takže různé vlnové délky se uvnitř hranolu šíří různou rychlostí, což způsobuje jejich lom pod různými úhly. Matematický vztah, který popisuje, jak se rychlost světla v prostředí mění v závislosti na vlnové délce, se nazývá disperzní vztah.

Nerovnoměrná médiaEdit

Různé lokální vlnové délky v závislosti na hřebeni oceánské vlny blížící se k pobřeží

Vlnová délka může být užitečným pojmem, i když vlna není periodická v prostoru. Například v oceánské vlně blížící se ke břehu, znázorněné na obrázku, se přicházející vlna vlní s různou lokální vlnovou délkou, která částečně závisí na hloubce mořského dna v porovnání s výškou vlny. Analýzu vlny lze založit na porovnání místní vlnové délky s místní hloubkou vody.

Sinusová vlna pohybující se v nerovnoměrném prostředí, se ztrátami

Vlny, které jsou sinusové v čase, ale šíří se prostředím, jehož vlastnosti se mění s polohou (nehomogenní prostředí), se mohou šířit rychlostí, která se mění s polohou, a v důsledku toho nemusí být sinusové v prostoru. Obrázek vpravo ukazuje příklad. Jak se vlna zpomaluje, vlnová délka se zkracuje a amplituda roste; za místem maximální odezvy je krátká vlnová délka spojena s velkými ztrátami a vlna zaniká.

Analýza diferenciálních rovnic takových systémů se často provádí přibližně, pomocí metody WKB (známé také jako Liouvilleova-Greenova metoda). Tato metoda integruje fázi v prostoru pomocí lokálního vlnového čísla, které lze interpretovat jako údaj o „lokální vlnové délce“ řešení jako funkci času a prostoru. tato metoda zachází se systémem lokálně, jako by byl homogenní s lokálními vlastnostmi; zejména lokální vlnová rychlost spojená s frekvencí je jediná věc potřebná k odhadu příslušného lokálního vlnového čísla nebo vlnové délky. Kromě toho metoda počítá pomalu se měnící amplitudu, aby splnila další omezení rovnic nebo fyzikálního systému, například pro zachování energie ve vlně.

CrystalsEdit

Vlnu na řadě atomů lze interpretovat podle různých vlnových délek.

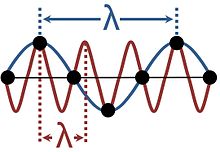
Vlny v krystalických pevných látkách nejsou spojité, protože se skládají z kmitů diskrétních částic uspořádaných v pravidelné mřížce. To způsobuje aliasing, protože stejnou vibraci lze považovat za vibraci s různými vlnovými délkami, jak je znázorněno na obrázku. Popisy využívající více než jednu z těchto vlnových délek jsou nadbytečné; je obvyklé zvolit nejdelší vlnovou délku, která odpovídá danému jevu. Rozsah vlnových délek postačující k popisu všech možných vln v krystalickém prostředí odpovídá vlnovým vektorům omezeným na Brillouinovu zónu.

Tato neurčitost vlnové délky v pevných látkách je důležitá při analýze vlnových jevů, jako jsou energetické pásy a mřížkové vibrace. Matematicky je ekvivalentní aliasingu signálu, který je vzorkován v diskrétních intervalech.