Hullámhossz
Lineráris közegben bármely hullámmintázat leírható szinuszos komponensek független terjedésével. Egy állandó v sebességgel terjedő szinuszos hullámforma λ hullámhossza a következővel adódik:
λ = v f , {\displaystyle \lambda ={\frac {v}{f}}}\,\,,}

ahol v a hullám fázissebességének (a fázissebesség nagysága), f pedig a hullám frekvenciája. Egy diszperzív közegben maga a fázissebesség függ a hullám frekvenciájától, így a hullámhossz és a frekvencia közötti kapcsolat nemlineáris.
Elektromágneses sugárzás – például a fény – esetében a szabad térben a fázissebesség a fény sebessége, kb. 3×108 m/s. Így egy 100 MHz-es elektromágneses (rádió)hullám hullám hullámhossza kb: 3×108 m/s osztva 108 Hz-cel = 3 méter. A látható fény hullámhossza a mélyvöröstől, nagyjából 700 nm-től az ibolyaszínig, nagyjából 400 nm-ig terjed (további példákért lásd: elektromágneses spektrum).
A levegőben lévő hanghullámok esetében a hangsebesség 343 m/s (szobahőmérsékleten és légköri nyomáson). Az emberi fül számára hallható hangfrekvenciák (20 Hz-20 kHz) hullámhossza tehát körülbelül 17 m és 17 mm között van. A denevérek valamivel magasabb frekvenciákat használnak, hogy 17 mm-nél kisebb célpontokat is fel tudjanak oldani. A hallható hang hullámhosszai sokkal hosszabbak, mint a látható fény hullámhosszai.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Például egy elektromágneses hullám esetében, ha a doboz ideális fémfalakkal rendelkezik, akkor a falaknál lévő csomópontokra vonatkozó feltétel azért adódik, mert a fémfalak nem bírják el az érintőleges elektromos teret, így a hullám amplitúdója a falnál nulla lesz.
Az álló hullám két ellentétes irányú sebességű szinuszos hullám összegének tekinthető. Következésképpen a hullámhossz, a periódus és a hullámsebesség ugyanúgy összefügg, mint a mozgó hullám esetében. Például a fénysebesség meghatározható egy ideális vákuumot tartalmazó fémdobozban álló hullámok megfigyeléséből.
Matematikai ábrázolásSzerkesztés
A v (x irányú) sebességük, f frekvenciájuk és λ hullámhosszuk alapján gyakran ábrázolják matematikailag:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) ) = A cos ( 2 π λ λ ( x – v t ) ) = A cos ( 2 π λ ( x – v t ) ) {\displaystyle y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)}

ahol y a hullám értéke bármely x helyzetben és t időben, A pedig a hullám amplitúdója. Általában a k hullámszám (a hullámhossz reciprokának 2π-szerese) és az ω szögfrekvencia (a frekvencia 2π-szerese) függvényében is kifejezik a következőképpen:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) ) {\displaystyle y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)}

melyben a hullámhossz és a hullámszám a sebességgel és a frekvenciával a következőképpen függ össze:
k = 2 π λ = 2 π f v = ω v , {\displaystyle k={\frac {2\pi }{\lambda }}}={\frac {2\pi f}{v}}={\frac {\omega }{v}},}

vagy
λ = 2 π k = 2 π v ω = v f . {\displaystyle \lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.}

A fent megadott második formában a fázist (kx – ωt) gyakran általánosítják (k-r – ωt)-ra, a k hullámszámot egy hullámvektorral helyettesítve, amely egy síkhullám irányát és hullámszámát adja meg a 3-térben, amelyet az r helyvektorral paraméterezünk. Ebben az esetben a k hullámszám, a k nagysága továbbra is a hullámhosszal áll a fentiekben bemutatott viszonyban, a v pedig a hullámvektor irányában skaláris sebességként értelmezhető. Az első forma, amely a fázisban a hullámhossz reciprokát használja, nem olyan könnyen általánosítható tetszőleges irányú hullámra.
A más fázisú szinuszokra és komplex exponenciálisokra való általánosítások is gyakoriak; lásd síkhullám. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. Nevezetesen, a fény sebessége egy közegben kisebb, mint a vákuumban, ami azt jelenti, hogy ugyanaz a frekvencia rövidebb hullámhossznak felel meg a közegben, mint a vákuumban, amint azt a jobb oldali ábra mutatja.
Ez a sebességváltozás a közegbe való belépéskor fénytörést, vagyis a közegek közötti határfelülettel ferdén találkozó hullámok irányának megváltozását okozza. Az elektromágneses hullámok esetében ezt a terjedési szögváltozást a Snell-törvény szabályozza.
A hullámsebesség az egyik közegben nemcsak eltérhet a másik közegben mért sebességtől, hanem a sebesség jellemzően a hullámhosszal is változik. Ennek következtében a hullám hullámhosszával együtt változik az irányváltozás is egy másik közegbe való belépéskor.
Elektromágneses hullámok esetében egy közegben a sebességet a közeg törésmutatója határozza meg a
v = c n ( λ 0 ) , {\displaystyle v={\frac {c}{n(\lambda _{0})}},}

ahol c a fény sebessége vákuumban, n(λ0) pedig a közeg törésmutatója λ0 hullámhosszon, ahol ez utóbbit nem a közegben, hanem vákuumban mérjük. A közegben a megfelelő hullámhossz
λ = λ 0 n ( λ 0 ) . {\displaystyle \lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.}

Az elektromágneses sugárzás hullámhosszának megadásakor általában a vákuumban mért hullámhosszt értjük, kivéve, ha a hullámhossz kifejezetten valamilyen más közegben mért hullámhosszként van megadva. Az akusztikában, ahol a hullámok létezéséhez elengedhetetlen a közeg, a hullámhossz értékét egy meghatározott közegre adják meg.
A fénysebesség hullámhosszal való változását diszperziónak nevezzük, és ez felelős azért az ismert jelenségért is, amikor a fényt egy prizma színkomponensekre választja szét. A szétválasztás akkor következik be, amikor a prizmán belül a törésmutató a hullámhosszal változik, így a különböző hullámhosszok különböző sebességgel terjednek a prizmán belül, ami miatt különböző szögben törnek meg. A matematikai összefüggést, amely leírja, hogyan változik a fény sebessége egy közegben a hullámhossz függvényében, diszperziós összefüggésnek nevezzük.
Nem egyenletes közegekSzerkesztés

A hullámhossz akkor is hasznos fogalom lehet, ha a hullám nem periodikus a térben. Például az ábrán látható, parthoz közeledő óceáni hullámban a beérkező hullám változó helyi hullámhosszal hullámzik, amely részben a tengerfenék mélységétől függ a hullámmagassághoz képest. A hullám elemzése a helyi hullámhossz és a helyi vízmélység összehasonlításán alapulhat.

Az időben szinuszos, de olyan közegben terjedő hullámok, amelyek tulajdonságai a helyzettel változnak (inhomogén közeg), a helyzettel változó sebességgel terjedhetnek, és ennek következtében nem feltétlenül szinuszosak a térben. A jobb oldali ábra egy példát mutat. A hullám lassulásával a hullám hullámhossza rövidül, az amplitúdó pedig nő; egy maximális válaszhely után a rövid hullámhossz nagy veszteséggel jár, és a hullám elhal.
Az ilyen rendszerek differenciálegyenleteinek analízise gyakran közelítőleg, a WKB-módszer (más néven Liouville-Green-módszer) segítségével történik. A módszer a fázist térben integrálja egy lokális hullámszám segítségével, amely úgy értelmezhető, hogy a megoldás “lokális hullámhosszát” jelzi az idő és a tér függvényében. ez a módszer lokálisan úgy kezeli a rendszert, mintha az egységes lenne a helyi tulajdonságokkal; különösen a frekvenciához tartozó lokális hullámsebesség az egyetlen, ami szükséges a megfelelő lokális hullámszám vagy hullámhossz becsléséhez. Ezenkívül a módszer lassan változó amplitúdót számol, hogy kielégítse az egyenletek vagy a fizikai rendszer egyéb kényszerfeltételeit, például a hullámban lévő energia megőrzéséhez.
CrystalsEdit
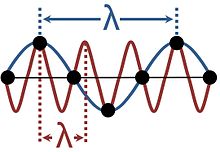
A kristályos szilárd testekben a hullámok nem folytonosak, mert szabályos rácsba rendezett diszkrét részecskék rezgéseiből állnak. Ez aliasinget eredményez, mivel ugyanazt a rezgést többféle hullámhosszúságúnak tekinthetjük, ahogy az ábrán látható. Az egynél több ilyen hullámhosszt használó leírások redundánsak; a jelenséghez illő leghosszabb hullámhosszt szokás kiválasztani. A kristályos közegben az összes lehetséges hullám leírásához elegendő hullámhossz-tartomány megfelel a Brillouin-zónára korlátozott hullámvektoroknak.
A hullámhossznak ez a meghatározatlansága a szilárd testekben fontos az olyan hullámjelenségek elemzésében, mint az energiasávok és a rácsrezgések. Ez matematikailag egyenértékű a diszkrét időközönként mintavételezett jel aliasingjével.