波長
線形媒体では、どんな波パターンも正弦波成分の独立した伝播という観点から記述することができます。 一定速度vで進む正弦波波形の波長λは、次の式で与えられます
λ = v f , {displaystyle \lambda ={frac {v}{f}},\,,}

ここでvは波の位相速度(の大きさ)、fは波の周波数と呼ばれるものです。
自由空間における光などの電磁波の場合、位相速度は光速であり、約3×108 m/sである。 したがって、100MHzの電磁波(ラジオ)の波長は、約 3×108 m/s÷108Hz=3mとなります。
空気中の音波の場合、音速は343 m/s(室温、大気圧の場合)です。
空気中の音波の場合、音速は343m/s(室温、大気圧)であり、人間の耳に聞こえる音の周波数(20Hz~20kHz)の波長はそれぞれ約17m~17mmとなります。 コウモリは、17mmより小さい対象を識別するために、もう少し高い周波数を使用している。


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. たとえば、電磁波の場合、ボックスに理想的な金属の壁がある場合、金属の壁は接線電場をサポートできないので、壁でのノードに対する条件は、壁でゼロ振幅を持つことを強制します。
定常波は、反対方向に速度がある 2 つの進行正弦波の合計と見なすことができます。 その結果、波長、周期、波速度は、進行波と同じように関係します。
数学的表現
進行する正弦波は、その速度 v (x 方向)、周波数 f、および波長 λ の観点から、次のようにしばしば数学的に表されます:
y ( x , t ) = A cos ( 2π ( x λ – f t ) ) = A cos ( 2π λ ( x – v t ) ) 。 {displaystyle y(x,\ t)=Acos \left(2﹁﹂({frac {x}{lambda }}-ftright})=Acos \left({frac {2pi }{lambda }}(x-vt)\right)}

ここでyは任意の位置x、時間tでの波の値、Aは波の振幅を表しています。 また、波数k(波長の逆数の2π倍)と角周波数ω(周波数の2π倍)で表すと、
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) ) となるのが一般的です。 {displaystyle y(x,\ t)=A\cos \left(kx-omega tentaright)=A\cos \left(k(x-vt)\right)}
 k = 2 π λ = 2 π f v = ω v , {displaystyle k={frac {2π }{lambda }}={frac {2π f}{v}}={frac {mega }{v}},}
k = 2 π λ = 2 π f v = ω v , {displaystyle k={frac {2π }{lambda }}={frac {2π f}{v}}={frac {mega }{v}},}

λ = 2 π k = 2 π v ω = v f . {

上記の2番目の形式では、波数kを、位置ベクトルrをパラメータとする3空間の平面波の方向と波数を指定する波ベクトルに置き換えることにより、位相 (kx – ωt) はしばしば (k-r – ωt) に一般化されています。 その場合も、波数kの大きさは、上に示したような波長との関係にあり、vは波動ベクトルの方向のスカラー速度と解釈されます。 位相に波長の逆数を用いた第一形式は、任意方向の波にはそう簡単に一般化できません。
他の位相の正弦波や、複素指数への一般化も一般的で、平面波を参照。 The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates.
媒質に入ったときのこの速度の変化は、屈折、つまり媒質間の界面に斜めにぶつかった波の向きを変える原因となります。
ある媒質での波の速度は、別の媒質での速度と異なる場合があるだけでなく、速度は通常、波長によって変化します。
ある媒質での波の速度は、別の媒質での速度と異なるだけでなく、一般に波長によって変化します。その結果、別の媒質に入ったときの方向の変化は、波の波長によって変化します。
電磁波の場合、媒質内の速度はその屈折率によって
v = c n ( λ 0 ) , {displaystyle v={frac {c}{n(\lambda _{0})}}, }

ここで、c は真空中の光速、n(λ0) は波長 λ0 における媒質の屈折率で、後者は媒質中ではなく真空中で測定されます。 媒質中の対応する波長は
λ = λ 0 n ( λ 0 ) . {Ίταν για ={ γfrac { γlambda _{0}}{n(γlambda _{0})}}.}.

電磁波の波長が引用される場合、他の媒体での波長と明記されていない限り、通常は真空中の波長を意図しています。
波長による光の速度の変化は分散と呼ばれ、プリズムで光が色に分離する現象は、この分散が原因となっています。 プリズム内部の屈折率が波長によって異なるため、プリズム内部では波長の異なる光が異なる速度で伝播し、異なる角度で屈折することで分離が起こります。 このように、媒質内の光の速度が波長によって変化することを表す数学的な関係を分散関係と呼びます。
Nonuniform mediaEdit

波が空間で周期的ではない場合でも波長は役に立つ概念になることがあります。 たとえば、図に示す海岸に近づく海洋波では、入ってくる波は、波高と比較して海底の深さに部分的に依存する、変化する局所波長でうねる。 この波長を水深と比較することで、波浪を解析することができます。

時間的に正弦波であっても、位置によって特性が異なる媒質 (不均質な媒質) を伝播する波は、位置によって異なる速度で伝播し、結果として空間的に正弦波でなくなることがあります。 右の図にその例を示します。
このような系の微分方程式の解析は、WKB 法 (Liouville-Green 法とも呼ばれる) を用いて、近似的に行われることが多いようです。 この方法は、局所的な波数を使って空間を通して位相を積分するもので、時間と空間の関数としての解の「局所的な波長」を示すと解釈できます。この方法は、システムを局所的な特性で均一であるかのように扱います。特に、ある周波数と関連する局所的な波速度は、対応する局所波数または波長を推定するために必要な唯一のものです。 さらに、この方法では、波のエネルギー保存など、方程式や物理システムの他の制約を満たすように、ゆっくりと変化する振幅を計算する。
CrystalsEdit
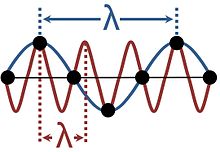
結晶固体の波は、規則的な格子に配置された離散的な粒子の振動で構成されているため、連続的ではありません。 そのため、図のように同じ振動でもさまざまな波長が考えられるので、エイリアシングが発生します。 複数の波長を用いて記述すると冗長になるため、現象に合った最も長い波長を選択するのが一般的である。
固体におけるこの波長の不定性は、エネルギーバンドや格子振動などの波動現象の解析において重要である。 数学的には、離散的な間隔でサンプリングされた信号のエイリアシングと等価である。