Długość fali
W ośrodkach liniowych dowolny przebieg falowy można opisać w kategoriach niezależnego rozchodzenia się składowych sinusoidalnych. Długość fali λ fali sinusoidalnej poruszającej się ze stałą prędkością v dana jest wzorem
λ = v f , {{displaystyle ˆlambda ={frac {v}{f}}},,}

gdzie v nazywamy prędkością fazową (wielkością prędkości fazowej) fali, a f jest częstotliwością fali. W ośrodku dyspersyjnym prędkość fazowa zależy od częstotliwości fali, co sprawia, że związek między długością fali a częstotliwością jest nieliniowy.
W przypadku promieniowania elektromagnetycznego – takiego jak światło – w wolnej przestrzeni prędkość fazowa jest równa prędkości światła, czyli około 3×108 m/s. Tak więc długość fali elektromagnetycznej (radiowej) o częstotliwości 100 MHz wynosi około: 3×108 m/s podzielone przez 108 Hz = 3 metry. Długość fali światła widzialnego waha się od głębokiej czerwieni, około 700 nm, do fioletu, około 400 nm (inne przykłady, zobacz widmo elektromagnetyczne).
Dla fal dźwiękowych w powietrzu, prędkość dźwięku wynosi 343 m/s (w temperaturze pokojowej i ciśnieniu atmosferycznym). Długości fal dźwięków o częstotliwościach słyszalnych dla ludzkiego ucha (20 Hz-20 kHz) wynoszą zatem odpowiednio od około 17 m do 17 mm. Nietoperze wykorzystują nieco wyższe częstotliwości, dzięki czemu mogą rozpoznawać cele mniejsze niż 17 mm. Długości fal w słyszalnym dźwięku są znacznie dłuższe niż te w świetle widzialnym.


Standing wavesEdit
A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.
The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. Na przykład, dla fali elektromagnetycznej, jeżeli pudełko ma idealne metalowe ściany, warunek posiadania węzłów na ścianach wynika z tego, że metalowe ściany nie mogą utrzymać stycznego pola elektrycznego, zmuszając falę do posiadania zerowej amplitudy na ścianie.
Fala stacjonarna może być postrzegana jako suma dwóch podróżujących fal sinusoidalnych o przeciwnie skierowanych prędkościach. W konsekwencji, długość fali, okres i prędkość fali są powiązane tak samo jak w przypadku fali podróżującej. Na przykład, prędkość światła można wyznaczyć na podstawie obserwacji fal stojących w metalowym pudełku zawierającym idealną próżnię.
Odwzorowanie matematyczneEdit
Przemieszczające się fale sinusoidalne są często przedstawiane matematycznie pod względem ich prędkości v (w kierunku x), częstotliwości f i długości fali λ jako:
y ( x , t ) = A cos ( 2 π ( x λ – f t ) = A cos ( 2 π λ ( x – v t ) ) {{displaystyle y(x,\ t)=Acos \left(2\pi \left({\frac {x}{lambda }}-ft\right)\right)=Acos \left({\frac {2\pi }{lambda }}(x-vt)\right)}

gdzie y jest wartością fali w dowolnym położeniu x i czasie t, a A jest amplitudą fali. Są one również powszechnie wyrażane w kategoriach liczby falowej k (2π razy odwrotność długości fali) i częstotliwości kątowej ω (2π razy częstotliwość) jako:
y ( x , t ) = A cos ( k x – ω t ) = A cos ( k ( x – v t ) { }

w którym długość fali i liczba falowa są związane z prędkością i częstotliwością jako:
k = 2 π λ = 2 π f v = ω v , { {displaystyle k={{frac {2pi }{lambda }}={{frac {2pi f}{v}}={frac {{omega }{v}}

lub
λ = 2 π k = 2 π v ω = v f . {{displaystyle {{lambda ={{frac {2}pi }{k}}={{frac {2}pi v}{{omega}}}={{frac {v}{f}}}.

W drugiej postaci podanej powyżej, faza (kx – ωt) jest często uogólniana do (k-r – ωt), poprzez zastąpienie liczby falowej k wektorem falowym, który określa kierunek i liczbę falową fali płaskiej w 3 przestrzeni, parametryzowanej przez wektor położenia r. W takim przypadku liczba falowa k, czyli wielkość k, pozostaje w tej samej relacji z długością fali, jak pokazano powyżej, przy czym v jest interpretowane jako prędkość skalarna w kierunku wektora falowego. Pierwsza forma, używająca odwrotności długości fali w fazie, nie generalizuje się tak łatwo do fali w dowolnym kierunku.
Generalizacje do sinusoid o innych fazach i do wykładników złożonych są również powszechne; zobacz fala płaska. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
A e i ( k x − ω t ) . {\displaystyle Ae^{i\left(kx-\omega t\right)}.}

General mediaEdit



The speed of a wave depends upon the medium in which it propagates. W szczególności, prędkość światła w ośrodku jest mniejsza niż w próżni, co oznacza, że tej samej częstotliwości będzie odpowiadać krótsza długość fali w ośrodku niż w próżni, jak pokazano na rysunku po prawej stronie.
Ta zmiana prędkości po wejściu do ośrodka powoduje refrakcję, czyli zmianę kierunku fal, które napotykają interfejs między ośrodkami pod kątem. Dla fal elektromagnetycznych, ta zmiana kąta propagacji jest regulowana przez prawo Snella.
Prędkość fali w jednym ośrodku nie tylko może się różnić od tej w innym, ale prędkość zazwyczaj zmienia się wraz z długością fali. W związku z tym zmiana kierunku po wejściu do innego ośrodka zmienia się wraz z długością fali.
Dla fal elektromagnetycznych prędkość w ośrodku jest regulowana przez jego współczynnik załamania zgodnie z
v = c n ( λ 0 ) , {

gdzie c jest prędkością światła w próżni, a n(λ0) jest współczynnikiem załamania ośrodka przy długości fali λ0, gdzie ten ostatni jest mierzony w próżni, a nie w ośrodku. Odpowiednia długość fali w ośrodku wynosi
λ = λ 0 n ( λ 0 ) . {{displaystyle λ ={frac {{lambda _{0}}}{n(λ 0})}}.

Gdy podaje się długość fali promieniowania elektromagnetycznego, zwykle ma się na myśli długość fali w próżni, chyba że długość fali jest wyraźnie określona jako długość fali w jakimś innym ośrodku. W akustyce, gdzie medium jest niezbędne do istnienia fal, wartość długości fali jest podawana dla określonego medium.
Zmiana prędkości światła z długością fali jest znana jako dyspersja i jest również odpowiedzialna za znane zjawisko, w którym światło jest rozdzielane na kolory składowe przez pryzmat. Separacja występuje, gdy współczynnik załamania wewnątrz pryzmatu zmienia się wraz z długością fali, więc różne długości fali propagują się z różnymi prędkościami wewnątrz pryzmatu, powodując ich załamanie pod różnymi kątami. Matematyczna zależność, która opisuje jak prędkość światła w medium zmienia się z długością fali jest znana jako zależność dyspersji.
Niejednorodne mediaEdit

Długość fali może być użytecznym pojęciem, nawet jeśli fala nie jest okresowa w przestrzeni. Na przykład, w fali oceanicznej zbliżającej się do brzegu, pokazanej na rysunku, fala przychodząca faluje ze zmienną lokalną długością fali, która zależy częściowo od głębokości dna morskiego w porównaniu z wysokością fali. Analiza fali może być oparta na porównaniu lokalnej długości fali z lokalną głębokością wody.

Fale, które są sinusoidalne w czasie, ale rozchodzą się w ośrodku, którego właściwości zmieniają się w zależności od położenia (ośrodek niejednorodny), mogą rozchodzić się z prędkością, która zmienia się w zależności od położenia, a w rezultacie mogą nie być sinusoidalne w przestrzeni. Rysunek po prawej stronie pokazuje przykład. Gdy fala zwalnia, długość fali skraca się, a amplituda rośnie; po miejscu maksymalnej odpowiedzi, krótka długość fali wiąże się z dużą stratą i fala wygasa.
Analiza równań różniczkowych takich układów jest często wykonywana w przybliżeniu, przy użyciu metody WKB (znanej również jako metoda Liouville’a-Greena). Metoda ta integruje fazę w przestrzeni za pomocą lokalnej liczby falowej, która może być interpretowana jako wskazanie „lokalnej długości fali” rozwiązania w funkcji czasu i przestrzeni. Metoda ta traktuje system lokalnie, tak jakby był jednorodny z lokalnymi właściwościami; w szczególności, lokalna prędkość fali związana z częstotliwością jest jedyną rzeczą potrzebną do oszacowania odpowiedniej lokalnej liczby falowej lub długości fali. Dodatkowo, metoda oblicza powoli zmieniającą się amplitudę, aby spełnić inne ograniczenia równań lub systemu fizycznego, takie jak zachowanie energii w fali.
CrystalsEdit
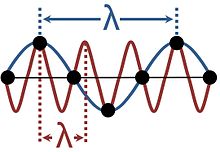
Fale w krystalicznych ciałach stałych nie są ciągłe, ponieważ składają się z drgań dyskretnych cząstek ułożonych w regularną siatkę. Powoduje to aliasing, ponieważ to samo drganie może być uważane za mające wiele różnych długości fal, jak pokazano na rysunku. Opisy wykorzystujące więcej niż jedną z tych długości fali są zbędne; konwencjonalne jest wybranie najdłuższej długości fali, która pasuje do zjawiska. Zakres długości fali wystarczający do opisu wszystkich możliwych fal w ośrodku krystalicznym odpowiada wektorom falowym ograniczonym do strefy Brillouina.
Ta nieokreśloność długości fali w ciałach stałych jest ważna w analizie zjawisk falowych, takich jak pasma energetyczne i drgania sieci. Jest to matematycznie równoważne aliasingowi sygnału, który jest próbkowany w dyskretnych odstępach czasu.